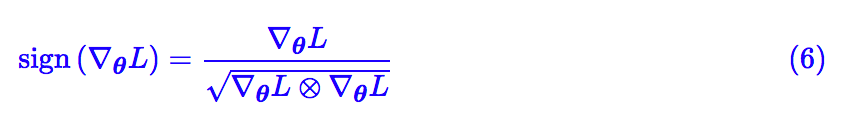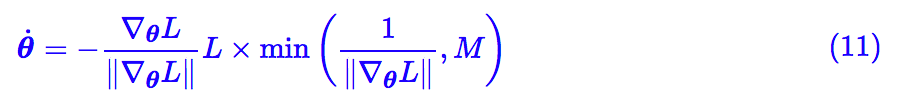会员服务 ·

从动力学角度看优化算法：一个更整体的视角

2019 年 1 月 28 日 黑龙江大学自然语言处理实验室

作者丨苏剑林

单位丨广州火焰信息科技有限公司

研究方向丨NLP，神经网络

个人主页丨kexue.fm

文章来源 | 公众号PaperWeekly

最近把优化算法跟动力学结合起来思考得越来越起劲了，这是优化算法与动力学系列的第三篇，我有预感还会有第四篇，敬请期待。

简单来个剧情回顾：第一篇中我们指出了其实 SGD 相当于常微分方程（ODE）的数值解法：欧拉法；第二篇我们从数值解法误差分析的角度，分析了为什么可以通过梯度来调节学习率，因此也就解释了 RMSprop、Adam 等算法中，用梯度调节学习率的原理。

本文将给出一个更统一的观点来看待这两个事情，并且试图回答一个更本质的问题：为什么是梯度下降？

注：本文的讨论没有涉及到动量加速部分。

梯度下降再述

前两篇文章讨论的观点是“梯度下降相当于解 ODE”，可是我们似乎还没有回答过，为什么是梯度下降？它是怎么来的？也就是说，之前我们只是在有了梯度下降之后，去解释梯度下降，还没有去面对梯度下降的起源问题。

下降最快的方向

基本的说法是这样的：梯度的反方向，是 loss 下降得最快的方向，所以要梯度下降。人们一般还会画出一个等高线图之类的示意图，来解释为什么梯度的反方向是loss下降得最快的方向。

因此，很多人诟病 RMSprop 之类的自适应学习率优化器的原因也很简单：因为它们改变了参数下降的方向，使得优化不再是往梯度方向下降，所以效果不好。

但这样解释是不是足够合理了呢？

再描述一下问题

正式讨论之前，我们把问题简单定义一下：

1. 我们有一个标量函数 L(θ)≥0，这里的参数 θ 可以是一个多元向量；

2. 至少存在一个点，使得，也就是说，L(θ) 的最小值就是 0；

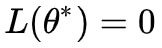
3. 给定 L(θ) 的具体形式，我们当然希望找到让 L(θ)=0 的 θ，就算不行，也希望找到一个 θ 让 L(θ) 尽量小一些。

值得一提的是第 2 点，它其实并不是必要的，但有助于我们后面描述的一些探讨。也就是说，第 2 点其实只是一个假设，要知道，随便给我们一个函数，要我们求最小值的位置，但一般来说我们并不能事先知道它的最小值是多少。

但是在深度学习中，这一点基本是成立的，因为我们通常会把 loss 设置成非负，并且得益于神经网络强大的拟合能力，loss 很大程度上都能足够接近于 0。

考虑loss的变化率

好，进入正题。假设在优化过程中参数 θ 按照某种轨迹 θ(t) 进行变化，那么 L(θ) 也变成了 t 的函数 L(θ(t))。注意这里的 t 不是真实的时间，它只是用来描述变化的参数，相当于迭代次数。

现在我们考虑 L(θ(t)) 的变化率：

这里就是 dθ/dt，⟨⋅⟩ 表示普通的内积。我们希望 L 越小越好，自然是希望上式右端为负数，而且绝对值越大越好。假如固定的模长，那么要使得上式右端最小，根据内积的特点，∇θL 和的夹角应该要是 180 度，也就是：

这也就说明了，梯度的反方向确实是 loss 下降最快的方向。而根据第一篇文章，上式不就是梯度下降？于是我们就很干脆地导出了梯度下降了。并且将 (2) 代入到 (1) 中，我们得到：

这表明，只要学习率足够小（模拟 ODE 模拟到足够准确），并且 ∇θL≠0，那么 L 就一定会下降，直到 ∇θL=0，这时候停留的位置，是个极小值点或者鞍点，理论上不可能是极大值点。

此外，我们经常用的是随机梯度下降，mini-batch 的做法会带来一定的噪声，而噪声在一定程度上能降低鞍点的概率（鞍点有可能对扰动不鲁棒），所以通常随机梯度下降效果比全量梯度下降要好些。

RMSprop再述

其实如果真的理解了上述推导过程，那么读者可以自己折腾出很多不同的优化算法出来。

不止有一个方向

比如，虽然前面已经证明了梯度的反方向是 loss 下降最快的方向，但凭什么就一定要往降得最快的的方向走呢？虽然梯度的反方向是堂堂正道，但也总有一些剑走偏锋的，理论上只要我保证能下降就行了，比如我可以取：

注意 ∇θL 是一个向量，sign(∇θL) 指的是对每一个分量取符号函数，得到一个元素是 -1 或 0 或 1 的向量。这样一来式 (1) 变为：

其中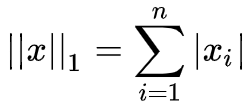表示向量的 L1 距离。这样选取也保证了 loss 在下降，理论上它收敛在 ∇θL=0 之处。

其实我们还有（假设梯度分量非零）:

结合 (4) 和第二篇文章，再配合滑动平均，可以发现这一节说的就是 RMSprop 算法。

也就是说，自适应学习率优化器中，“学习率变成了向量，使得优化方向不再是梯度方向”根本不是什么毛病，也就不应该是自适应学习率优化器被人诟病之处。

不走捷径会怎样

但事实上是，真的精细调参的话，通常来说自适应学习率最终效果真的是不如 SGD，说明自适应学习率优化器确实是有点毛病的。也就是说，如果你剑走偏锋，虽然一开始你走的比别人快，后期你就不如别人了。

毛病在哪呢？其实，如果是 Adagrad，那问题显然是“太早停下来了”，因为它将历史梯度求和了（而不是平均），导致后期学习率太接近 0 了；如果是上面说的 RMSprop，那么问题是——“根本停不下来”。

其实结合 (4) 和 (6) 我们得到：

这个算法什么时候停下来呢？实际上它不会停，因为只要梯度分量非零，那么对应的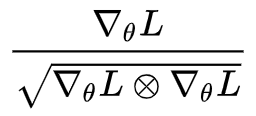的分量也非零（不是 1 就是 -1），从而在理论上看，这个算法并没有不动点，所以它根本不会停。

为了缓解这个情况，RMSprop 在实际使用的时候，采取了对分母滑动平均、加上 epsilon（防止除零错误）这两个技巧。

但这只能算是缓解了问题，用 ODE 的话说就是“这个 ODE 并不是渐近稳定的”，所以终究会经常与局部最优点插肩而过。这才是自适应学习率算法的问题。

一点捣鼓

前面说了，如果真的理解过这个过程，其实自己都可以捣鼓出一些“独创的”优化算法出来，顺便还分析收敛情况。下面介绍我自己的一个捣鼓过程，还让我误以为是一个能绝对找出全局最优点的优化器。

观看下面内容之前，请确保自己已经理解前述内容，否则可能造成误导。

以全局最优为导向

这个捣鼓的出发点在于，不管是 (2)（对应的收敛速率为 (3)）还是 (7)（对应的收敛速率为 (5)），就算它们能收敛，都只能保证 ∇θL=0 ，无法保证是全局最优点（也就是不一定能做到 L(θ)=0）。

于是一个很简单的想法是：既然我们已经知道了最小值是零，为什么不把这个信息加上去呢？

于是类比前面的思考过程，我们可以考虑：

这时候式 (1) 变得非常简单：

这只是一个普通的线性微分方程，而且解是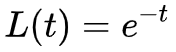，随着 t→+∞，L(t)→0，也就是说 loss 一定能收敛到零。

真有这样的好事？

当然没有，我们来看式 (8) ，如果跑到了一个局部最优点，满足 ∇θL=0, L>0，那么式 (8) 的右端就是负无穷了，这在理论上没有问题，但是在数值计算上是无法实现的。

开始我以为这个问题很容易解决，似乎对分母加个 epsilon 避开原点就行了。但进一步分析才发现，这个问题是致命性的。

为了观察原因，我们把式 (8) 改写为：

问题就在于 1/||∇θL|| 会变得无穷大（出现了奇点），那能不能做个截断？比如考虑：

其中 M≫0 是个常数，这样就绕开了奇点。这样子做倒是真的能绕开一些局部最优点，比如下面的例子：

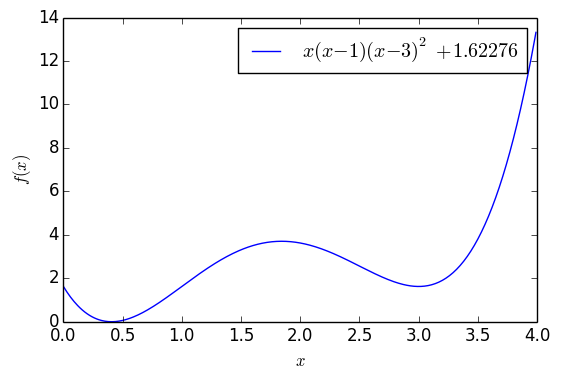
▲ 含有两个极小值点的一元函数

这个函数大约在 x=0.41 之间有一个全局最优点，函数值能取到 0，但是在 x=3 的时候有一个次最优点。如果以 x0=4 为初始值，单纯是用梯度下降的话，那么基本上都会收敛到 x=3，但是用 (11)，还是从 x0=4 出发，那么经过一定振荡后，最终能收敛到 x=0.41 附近：

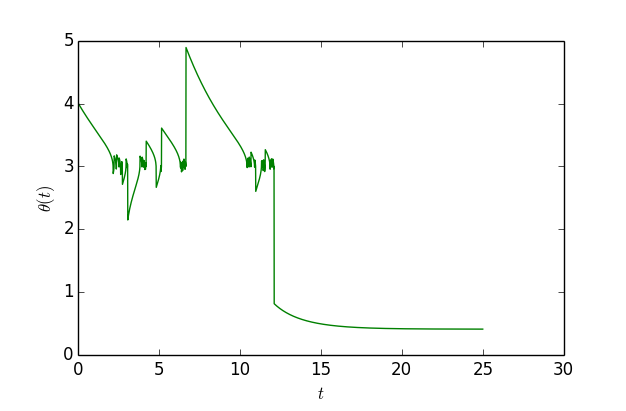
▲ 模拟“独创版”梯度下降轨迹

可以看到，开始确实会在 x=3 附近徘徊，振荡一段时间后就跳出来了，到了 x=0.41 附近。作图代码：

import numpy as np
import matplotlib.pyplot as plt


def f(x):
    return x * (x - 1) * (x - 3) * (x - 3) + 1.62276

def g(x):
    return -9 + 30 * x - 21 * x**2 + 4 * x**3

ts = [0]
xs = [4]
h = 0.01
H = 2500

for i in range(H):
    x = xs[-1]
    delta = -np.sign(g(x)) * min(abs(g(x)) / g(x)**2, 1000) * f(x)
    x += delta * h
    xs.append(x)
    ts.append(ts[-1] + h)

print f(xs[-1])
plt.figure()
plt.clf()
plt.plot(ts, xs, 'g')
plt.legend()
plt.xlabel('$t$')
plt.ylabel('$\theta(t)$')
plt.show()