如何深入理解矩阵？184页《矩阵分解与应用》2022新书全面阐述矩阵分解原理、体系与应用

2022 年 1 月 10 日 专知

矩阵分解与应用干货书，值得关注!

1954年，Alston S. Householder发表了《数值分析原理》，这是矩阵分解的第一个现代处理方法，它支持(块)LU分解——将矩阵分解为上三角矩阵和下三角矩阵的乘积。而现在，矩阵分解已经成为机器学习的核心技术，这在很大程度上是因为反向传播算法在拟合神经网络方面的发展。本调研的唯一目的是对数值线性代数和矩阵分析中的概念和数学工具进行一个完整的介绍，以便在后续章节中无缝地介绍矩阵分解技术及其应用。然而，我们清楚地认识到，我们无法涵盖所有关于矩阵分解的有用和有趣的结果，并且给出了这种讨论的范围的缺乏，例如，分离分析欧几里德空间、厄米特空间、希尔伯特空间和复域中的东西。我们建议读者参考线性代数领域的文献，以获得相关领域的更详细介绍。本综述主要是对矩阵分解方法的目的、意义，以及这些方法的起源和复杂性进行了总结，并阐明了它们的现代应用。最重要的是，本文为分解算法的大多数计算提供了改进的过程，这可能会降低它们所引起的复杂性。同样，这是一个基于分解的上下文，因此我们将在需要和必要时介绍相关的背景。在其他许多关于线性代数的教科书中，主要思想被讨论，而矩阵分解方法是“副产品”。然而，我们将重点放在分解方法上，而主要思想将作为分解方法的基本工具。数学的先决条件是线性代数的第一门课程。除了这个适中的背景，发展是独立的，提供了严格的证据。

https://www.zhuanzhi.ai/paper/a392240897ea63228b548b0570a315d4

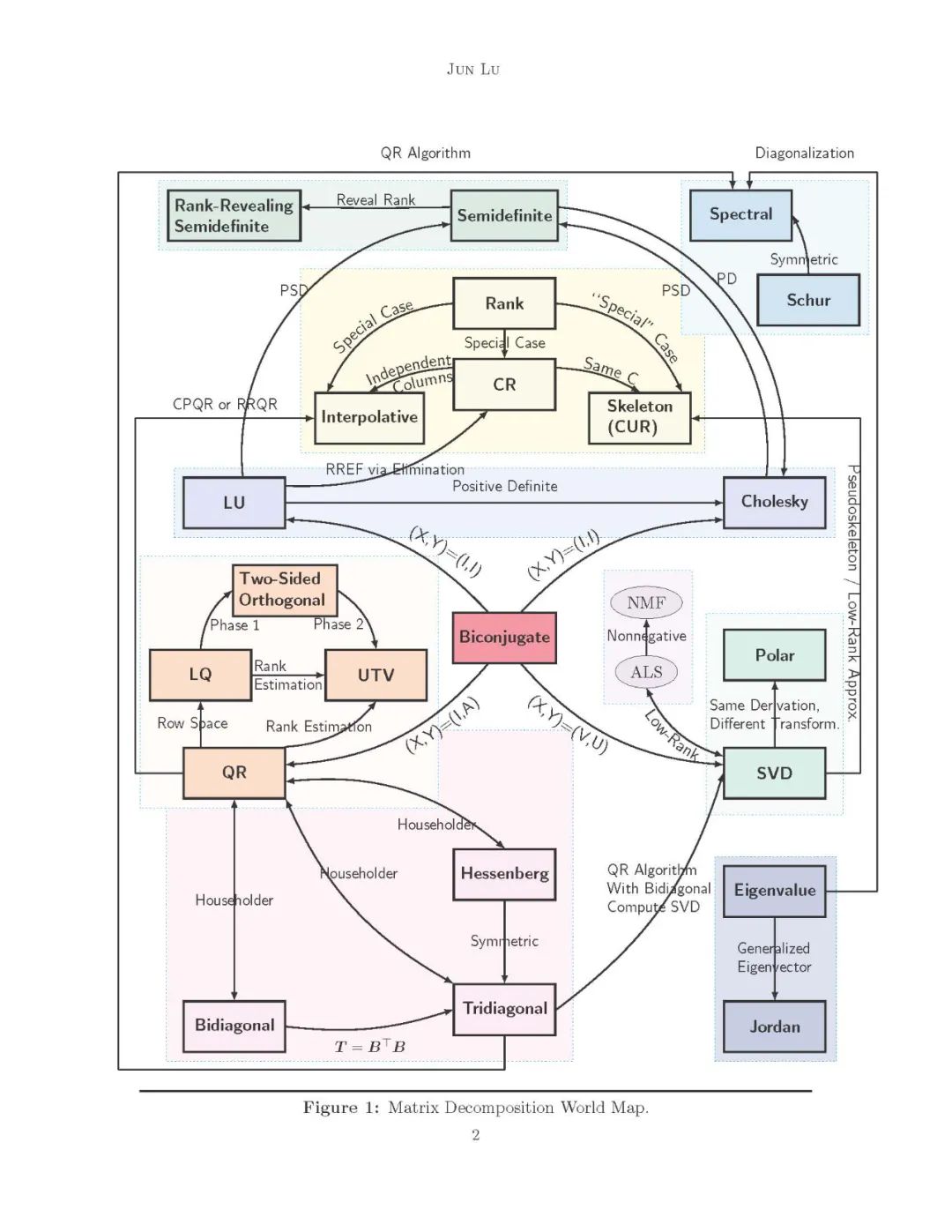
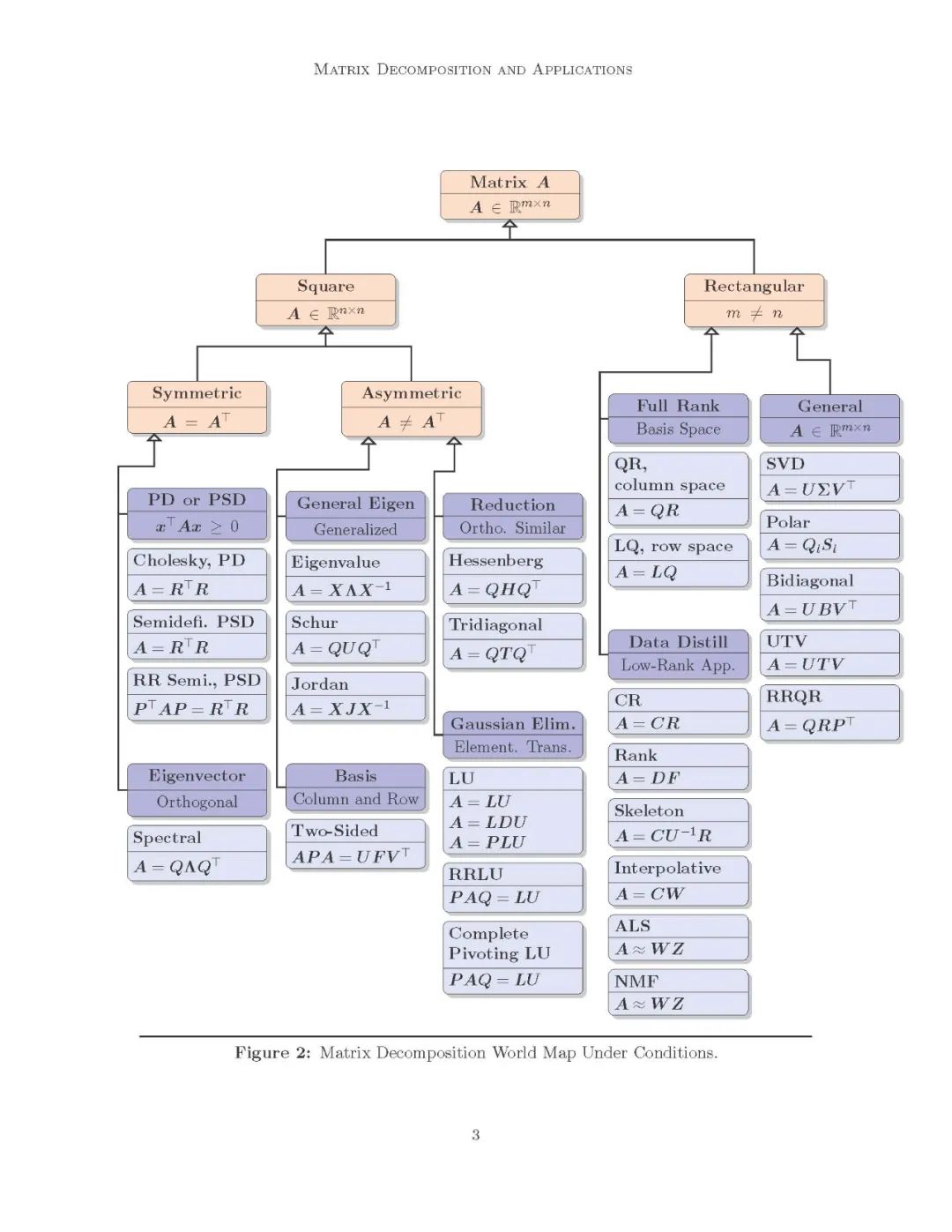
矩阵分解全景

矩阵分解已经成为统计学的核心技术(Banerjee和Roy, 2014;、优化(Gill et al.， 2021)、机器学习(Goodfellow et al.， 2016);而深度学习在很大程度上是由于反向传播算法在拟合神经网络和低秩神经网络在高效深度学习中的发展。本调查的唯一目的是对数值线性代数和矩阵分析中的概念和数学工具进行一个完整的介绍，以便在后续章节中无缝地介绍矩阵分解技术及其应用。然而，我们清楚地认识到，我们无法涵盖所有关于矩阵分解的有用和有趣的结果，并且给出了这种讨论的范围的缺乏，例如，欧氏空间、厄米特空间和希尔伯特空间的分离分析。我们建议读者参考线性代数领域的文献，以获得相关领域的更详细介绍。一些优秀的例子包括(Householder, 2006; Trefethen and Bau III, 1997; Strang, 2009; Stewart, 2000; Gentle, 2007; Higham, 2002; Quarteroni et al., 2010; Golub and Van Loan, 2013; Beck, 2017; Gallier and Quaintance, 2017; Boyd and Vandenberghe, 2018; Strang, 2019; van de Geijn and Myers, 2020; Strang, 2021)。最重要的是，本综述将只涵盖矩阵分解方法存在性的紧凑证明。关于如何降低计算复杂度，在各种应用和例子中进行严格的讨论，为什么每种矩阵分解方法在实践中都很重要，以及张量分解的初步研究，请参见(Lu, 2021c)。

矩阵分解是将一个复杂的矩阵分解成其组成部分的一种方法，这些组成部分的形式更简单。全局矩阵计算方法的基本原则是,它不是业务矩阵的algorithmists解决特定的问题,但这是一个方法,可以简化更复杂的矩阵运算,可以进行分解的部分而不是原始矩阵本身。

矩阵分解算法可以分为许多类。尽管如此，六个类别占据了中心，我们在这里概括一下:

1. 由高斯消去产生的因子分解包括LU分解和它的正定替代- Cholesky分解;

2. 将矩阵的列或行正交化时得到的因式分解，使数据可以用标准正交基很好地解释;

3.分解矩阵的骨架，使列或行的一个子集可以在一个小的重构误差中表示整个数据，同时，矩阵的稀疏性和非负性保持原样;

4. 化简为Hessenberg、三对角或双对角形式，结果是，矩阵的性质可以在这些化简矩阵中探索，如秩、特征值等;

5. 因式分解是计算矩阵特征值的结果;

6. 特别地，其余的可以被转换为一种特殊的分解，其中涉及到优化方法和高级思想，其中类别可能无法直接确定。