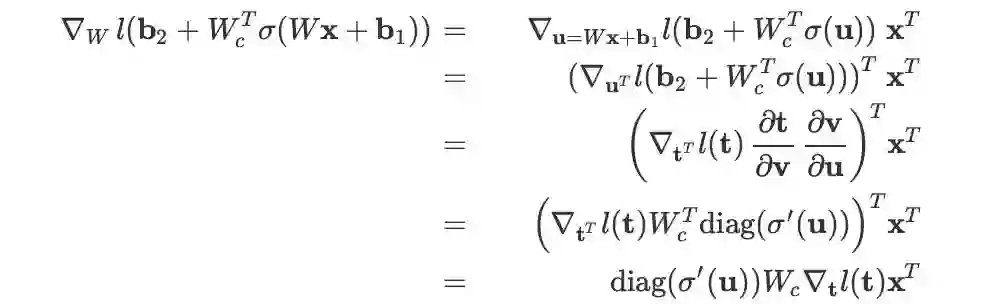机器之心最干的文章:机器学习中的矩阵、向量求导
作者:七月
本文的目标读者是想快速掌握矩阵、向量求导法则的学习者,主要面向矩阵、向量求导在机器学习中的应用。因此,本教程而非一份严格的数学教材,而是希望帮助读者尽快熟悉相关的求导方法并在实践中应用。另外,本教程假定读者熟悉一元函数的求导。
本文公式太多,微信上展示会有一些问题。所以本文适合读者了解矩阵、向量求导,而详细地学习与分析请下载本文的PDF版。
PDF 下载地址:https://pan.baidu.com/s/1pKY9qht
所谓矩阵求导,本质上只不过是多元函数求导,仅仅是把把函数的自变量以及求导的结果排列成了矩阵的形式,方便表达与计算 而已。复合函数的求导法则本质上也是多元函数求导的链式法则,只是将结果整理成了矩阵的形式。只是对矩阵的每个分量逐元素 地求导太繁琐而且容易出错,因此推导并记住一些常用的结论在实践中是非常有用的。
矩阵求导本身有很多争议,例如:
对于求导结果是否需要转置?
不同教材对此处理的结果不一样,这属于不同的 Layout Convention。本文以不转置为主,即求导结果与原矩阵/向量同型,术语叫 Mixed Layout。
矩阵对向量、向量对矩阵、矩阵对矩阵求导的结果是什么?
最自然的结果当然是把结果定义成三维乃至四维张量,但是这并不好算。也有一些绕弯的解决办法 (例如把矩阵抻成一个 向量等),但是这些方案都不完美 (例如复合函数求导的链式法则无法用矩阵乘法简洁地表达等)。在本教程中,我们认为,这三种情形下导数没有定义。凡是遇到这种情况,都通过其他手段来绕过,后面会有具体的示例。
因此,本教程的符号体系有可能与其他书籍或讲义不一致,求导结果也可能不一致 (例如相差一次矩阵转置,或者是结果矩阵是否平铺成向量等),使用者需自行注意。另外,本教程中有很多笔者自己的评论,例如关于变形的技巧、如何记忆公式、如何理解其他的教程中给出的和本教程中形式不同的结果等。
文中如有错漏,欢迎联系 ruanchong_ruby@163.com,我会尽快订正。
符号表示
标量用普通小写字母或希腊字母表示,如
等。
向量用粗体小写字母或粗体希腊字母表示,如 x 等,其元素记作
(注意这里
没有加粗。加粗的小写字母加下标,例如
等,表示这是两个不同的常数向量)。向量默认为列向量,行向量需要用列向量的转置表示,例如
等。
矩阵用大写字母表示,如A 等,其元素记作
(注意这里 a 用的是小写字母。大写字母加下标,例如
等,表示不同 的常数矩阵)。
用字母表中靠前的字母 (如 a,b,c等) 表示常量,用 f,g,h 或字母表中靠后的字母 (如u,v等)等表示变量或函数。
有特殊说明的除外。
综上所述,本文进行如下约定:
矩阵/向量值函数对实数的导数:
要点:求导结果与函数值同型,且每个元素就是函数值的相应分量对自变量
求导
若函数
,则
也是一个 m×n 维矩阵,且
,也可用劈形算子将导数记作
,或记作
。
由于向量是矩阵的特殊情形,根据上面的定义也可以得到自变量为向量时的定义:若函数
,则
是一个 m 维向量,且
。若函数值
是行向量则结果为行向量,可记作
;若函数值 f 是列向量则求导结果为列向量,可记作
。
注:本文开头即说明过,变量为向量时仅仅是将其看作多个实数,无所谓行向量与列向量之分。这里用行向量或列向量的 说法仅仅为了把公式用矩阵相乘的方式表示出来方便,因为在数学公式总要指定向量是行向量或者列向量中的某一个,才能与公式里的其他部分做矩阵运算时维度相容。下同。
实值函数对矩阵/向量的导数:
要点:求导结果与自变量同型,且每个元素就是f对自变量的相应分量求导
若函数
,则
也是一个 m×n 维矩阵,且
也可使用劈形算子将导数记作
。
由于向量是矩阵的特殊情形,根据上面的定义也可以得到自变量为向量时的定义:若函数
,则
也是一个 m 维向量,且
。若函数值
是行向量则结果为行向量,可记作
;若函数值 f 是列向量则求导结果为列向量,可记作
。
向量值函数对向量的导数(雅克比矩阵 ):
若函数
,则
是一个 m×n 维矩阵,且
。用劈形算子表示时可记作
。
注:如前所述,本教程仅仅是把变量都看成多个实数,无所谓行与列之分,因此在表述从向量
到
的雅克比矩阵时,不区分 x 或者 f 到底是行向量还是列向量,统一用
表示,维度也都是m-by-n。有些教程可能会区分 行对列、列对列、行对行、列对行几种不同情形的求导,认为有些结果相差一个转置,有些组合不能求导等等。本教程则认为只有一种求导结果,就是雅克比矩阵。
有一点需要注意的是,若f退化成标量
,则 x 到 f 的雅克比矩阵
是一个行向量,是梯度 (列向量) 的转置,即
。注意这里使用的记号:左边 f 加粗,是把它看做一个长度为 1 的向量,表示求向量 x 到向量 f 的雅克比矩阵;右边
为普通字体,表示实函数
对向量 x 的导数。
劈形算子
:
在求导的变量比较明确时,可以省略劈形算子的下标写成
。
劈形算子和偏导数两种记号大体上可以认为是相同的,只不过在涉及到变量分量的推导过程 (例如用链式法则推神经网络 的 BP 算法) 中,偏导数那一套符号更加常用;而劈形算子的优势是书写简单,在对传统的机器学习模型的目标函数求导 时,劈形算子有时更常用。
对于一个实函数
,其梯度记为
,也可记作gradf,是一个m 维向量。Hessian 矩阵记为
,其中
,是一个m×m的矩阵。根据上述定义可以发现,Hessian 矩阵其实是 X 到
的雅克比矩阵,因此
不光是一个形式记号,而是可以用
来计算。
注:某些教材区分对行向量和列向量求导,认为 Hessian 矩阵是先对行向量
求导,再对列向量X求导(或者反过来),因此写作
(或者
)。
对于一个实函数
,其梯度规定为 m×n 维矩阵
,Hessian 矩阵不作定义。
对上述约定的理解
对于实值函数 f,上面的定义满足转置关系(f 对某个变量和其转置的导数互为转置):即:(其中 x 代表任意维度的向量或矩阵)。
函数增量的线性主部与自变量增量的关系:
实值函数对矩阵/向量的导数:
,此式用到的技巧非常重要:两个同型矩阵对应元素相乘再求和时常用上面第二个等式转化为迹,从而简化表达和运算。从另一个角度讲,这是矩阵导数的另一种定义。即:对于函数
,若存在矩阵 A,使得
时(||*|| 为任意范数),成立
,则定义
。矩阵乘积的迹是一个线性算子。事实上,如果有两个同型矩阵 A、B,他们的内积即定义为 <A, B> = tr(A^T * B)。容易验证,向量内积也符合这个定义,因此此式可以看成是向量内积的推广。
实值函数对矩阵/向量的导数:,此式右边是向量内积,可看做前一个式子的退化情形。
向量值函数对向量的导数:
,此式即为重积分换元时用于坐标变换的Jacobian矩阵。
变量多次出现的求导法则
规则:若在函数表达式中,某个变量出现了多次,可以单独计算函数对自变量的每一次出现的导数,再把结果加起来。
这条规则很重要,尤其是在推导某些共享变量的模型的导数时很有用,例如 antoencoder with tied weights(编码和解码部分的权重矩阵互为转置的自动编码器)和卷积神经网络(同一个 feature map 中卷积核的权重在整张图上共享)等。
举例(该规则对向量和矩阵也是成立的,这里先用标量举一个简单的例子):假设函数表达式是 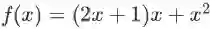
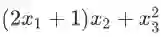
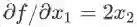
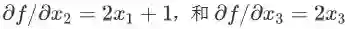
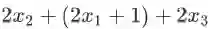
如果用计算图(computation graph,描述变量间依赖关系的示意图,后面会举例)的语言来描述本条法则,就是:若变量 x 有多条影响函数 f 的值的路径,则计算 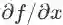
有了上面的基础,我们就可以推导 Batch normalization(以下简称 BN)的求导公式了。 BN 的计算过程为:
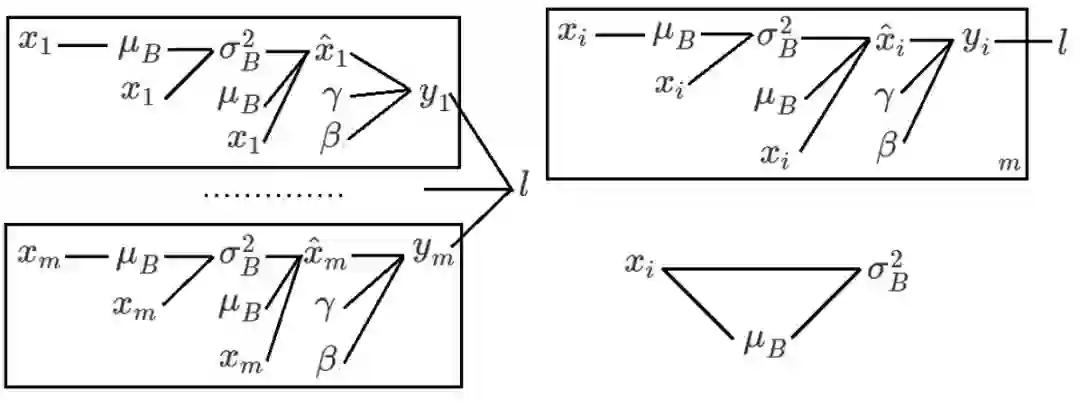
其中 m 是批的大小,x_1 到 x_m 分别是 m 个不同样本对于某个神经元的输入,l 是这个批的总的损失函数,所有变量都是标量。求导的第一步是画出变量依赖图,如下所示(根据左边的变量可以计算出右边的变量,如果为了强调,也可以在边上添加从左向右的箭头):
左侧,右上,右下分别是三种不同的画法(读者也可以尝试其他的画法):左边的图是把所有变量 x_i 都画了出来,比较清楚,如果想不清楚变量之间是如何相互依赖的,这样画可以帮助梳理思路;右上是我自创的一种方法,借鉴了概率图模型中的盘记号(plate notation),把带下标的变量用一个框框起来,在框的右下角指明重复次数;右下我只画了一个局部,只是为了说明在有些资料中,相同的变量(如本例中的 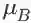
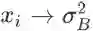
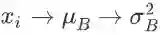
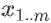
BN 原论文中也给出了反向传播的公式,不过我们不妨试着自己手算一遍:
x_i hat 影响损失函数只有唯一的路径
,根据链式法则,得到:
。
λ 影响损失函数有 m 条路径:对任意一个 i,
都是一条路径,需要对这些路径分别求导再加和:
。
partial l 除以 partial β 的计算与上面类似:
。
影响损失函数的路径也有 m 条:
(此处忽略中间变量 y_i,直接把 l 看成的 x_i hat 函数。)所以
。注意求导的时候把
当成一个整体,想象这就是一个字母,而不要把它想成标准差的平方。
影响损失函数共有 2m 条路径:
(分别对应于右上图中较短和较长的路径)。故有:
。其中最后一步的理由是根据
的定义,后一项为零。
影响损失函数有 3 条路径:
,所以
。
常用公式
向量求导的链式法则
易发现雅克比矩阵的传递性:若多个向量的依赖关系为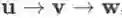
证明:只需逐元素求导即可。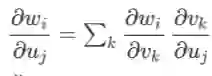
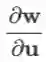
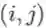
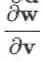
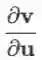
注:将两项乘积的和转化成向量内积或矩阵相乘来处理,是很常用的技巧。
雅克比矩阵的传递性可以很容易地推广到多层中间变量的情形,采用数学归纳法证明即可。
若中间变量都是向量,但最后的结果变量是一个实数,例如变量依赖关系形如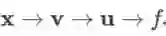
由雅克比矩阵的传递性知:
再根据 f 退化时雅克比矩阵和函数导数的关系,有:
以上三式相结合,可以得到如下链式法则:
上面的结果显然也可以推广到任意多层复合的情形(可用于 RNN 的 BPTT 的推导)。
上面的公式是把导数视为行向量(即以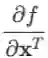
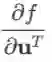
若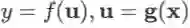
或写作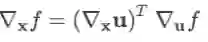
这里再给出一个特例:若变量依赖关系为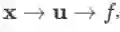
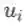
计算出而与 x 的其他分量无关,则易知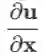
其中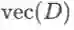

由于最终的结果是两个向量逐元素相乘,所以也可以交换一下相乘的顺序,写成:
本条规则在神经网络中也很常用,常见的情形包括但不限于:逐元素地应用激活函数
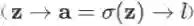
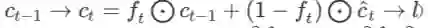
* 因为依赖关系简单,本公式也可以直接根据导数逐分量的定义直接推出来:
此即前述公式的分量形式。
记忆:只需记住结果是一堆雅克比矩阵的乘积,相乘的顺序根据维度相容原则调整即可(假设每个中间变量的维度都不一样,看怎么摆能把雅克比矩阵的维度摆成矩阵乘法规则允许的形式。只要把矩阵维度倒腾顺了,公式也就对了。)
注:网络上各种资料质量参差不齐,在其他教程中时常会见到向量对矩阵求导的表达式。例如介绍 RNN 的梯度消失问题的文章中,经常会见到
这种式子。如果文中出现这个式子是定性的,只是为了说明链式法则中出现了很多连乘项导致了梯度消失,那么读者也只需定性地理解即可。如果文中出现这个式子是定量的,是为了推导反向传播的公式,那么笔者建议读者用如下两种方式之一理解:
其一是把
理解成一种简写形式:先把 W 抻成一个向量,然后公式中的每一个雅克比矩阵就都可以计算了,最后再把结果向量重新整理成 W 的同型矩阵。但是这种方法非常复杂,因为把 W 抻成向量以后目标函数关于 W 的表达式就变了,很难推导
这个雅克比矩阵。一个具体的算例见《Optimizing RNN performance》(https://svail.github.io/rnn_perf/)一文中最后的推导。(如果你不打算熟练掌握这种方法,只浏览一下看看大意即可。相信我,如果你学了本文中的方法,你不会再想用这种把矩阵抻开的方法求导的。)
其二是把最后一项分母中的 W 理解成矩阵 W 中的任一个元素 w_ij,从而上述表达式中的四项分别是向量(此处看作行向量)、矩阵、矩阵、向量(列向量),从而该表达式可以顺利计算。但是这也很麻烦,因为得到的结果不是直接关于 W 的表达式,而是关于其分量的,最后还要合并起来。
其他理解方式,恕我直言,基本上都是作者自己就没弄懂瞎糊弄读者的。
实值函数对向量求导
未作特殊说明即为对变量 x 求导。
几个基本的雅克比矩阵:
,特别地,
。
向量内积的求导法则:
内积是一个实数,因此本节相当于实数对向量求导,结果是与自变量同型的向量。
这是最基本的公式,正确性是显然的,因为
。
正确性是显然的,因为
。另外,也可以用变量多次出现的求导法则结合上一条公式证明。
利用变量多次出现的求导法则以及前面的公式容易证明。另外,若 A 是对称矩阵,上式右边可以化简为 2A_x。
向量内积的求导法则:
利用变量多次出现的求导法则(x 同时在 u、v 中出现)+ 复合函数求导法则(列向量形式)易证。
向量数乘求导公式
推导:
,两边逐分量对比一下便知等式成立。
记忆:按两个标量函数相乘的求导法则记,再注意一下维度相容原理即可。向量数乘的结果还是一个向量,所以此处相当于向量对向量求导,结果是一个雅克比矩阵,形状为 f 的维度乘 x 的维度。
矩阵迹求导
未作特殊说明即为对 X 求导。迹是一个实数,所以相当于实数对矩阵求导,结果是一个和 X 同型的矩阵。
先回顾一下迹的基本性质:
线性性质:
转置不变性:
轮换不变性:
特别地,
。注意,轮换不变性不等于交换性。例如:
,但是一般情况下
。
基本公式:
推导:逐元素求导验证
:(事实上这个公式就是矩阵导数的另一种定义,前面也有叙述。)
根据此式容易得到另一个式子:
迹方法的核心公式(非常重要):
推导:利用变量多次出现的求导法则:
(X_c 表示将 X 的此次出现视作常数)
这个公式非常重要,在推导最小二乘解等问题上都会遇到。公式的名字是我瞎起的,我不知道它叫什么名字。
其他与矩阵迹有关的公式
大部分都是上述核心公式的简单推论,不必强记
推导:
注:将实数看作是 1*1 矩阵的迹是很常用的技巧。
推导:使用迹方法的核心公式。过程略。
推导:将左式的括号相乘展开,然后用上面的关于矩阵迹的公式。
推导同上,只需注意到
即可。特别地,
(此式也可逐元素求导直接验证)
行列式的求导公式:
实数对矩阵求导,结果是和 X 同型的矩阵。此条证明较繁琐,大致过程是用逐元素求导+伴随矩阵的性质推导,过程可参考 math overflow。最好能直接记住。
矩阵求导的链式法则
设
,则:
,或简写为
关于维度的说明:X 是矩阵,中间变量 U 也是矩阵(未必与 X 同型),最终结果 y 是实数。因此求导结果是和 X 同型的矩阵。
注:此式似乎用的不多,毕竟这仅仅是对 x_ij 这一个分量求导的结果,很难直接得到对 X 求导的结果。而且这个式子只是最基础的多元函数复合的链式法则而已,没有得到什么特别有趣或者重要的结论。
设
,则:
(等式右边是实数和矩阵的数乘)
关于维度的说明: X,u,y 分别是矩阵、实数、实数,因此相当于实数对矩阵求导,结果是 X 同型的矩阵。
证明是显然的,逐元素求导验证即可:
线性变换的导数(非常重要。由于线性变换很常用,记住此式可以简化很多公式的推导过程):
设有
及线性映射
(因此
),则:
推导:
,而
(
是 Kronecker delta 符号:若l=j 值为 1,否则为 0),将后式代入前式,得:
,即矩阵 A^T的第 i 行 和 矩阵
的第 j 列的内积。
向量的线性变换是上式的退化情形,即:
向量的线性变换还可以求二阶导:
推导:记
,则
记忆:同上,记住大概的形状(对线性变换来说,求一次导就是乘一个矩阵),然后根据维度相容原则摆顺了就行。
由于线性变换很常用,这里不妨把给 X 右乘一个矩阵时的公式一并给出,以便查阅:设有
及线性映射
(因此
),则:
证明:若令
,则变量依赖关系变为:
,且
,根据线性变换的求导法则,知:
,所以
。
记忆:先做线性变换再求导就等于先求导再做线性变换。剩下的细节(如左乘还是右乘等)根据维度相容原则倒腾即可。
注:此式很有用,在神经网络中,经常有形如
的依赖关系。其中 x 是神经网络某一层的输入数据(不是训练神经网络时要求导的变量!不过在构造对抗样本时可能需要对 x 求导), W,b 是该层的参数(这才是训练神经网络时要求导的变量),z 是经过变换后预备输入给下一层的值,l 是最终的损失函数。根据上述线性变换的求导公式,立即可以得到 BP 算法的核心步骤:
。(另注:标准的 BP 算法通常将
定义为变量δ。)
其他公式
这一部分在机器学习中遇到的不多(毕竟常见的情况是求一个标量损失函数对其他变量的导数),不是特别重要,不过偶尔在凸优化里会碰到一些。这里收集整理这几个式子主要是为了资料完整、查阅方便。以下假定 F 是可逆方阵:
自变量和函数值都是实数,求导结果也是实数。推导过程较困难,主要用到了矩阵的雅克比公式(不是雅克比矩阵)。建议记住,或者用时查表。
自变量和函数值都是实数,求导结果也是实数。
推导:根据最基本的一元函数复合的求导法则即可。令
,则:
。
矩阵对实数求导,结果是和 F^-1 同型的矩阵(也即和 F 同型的矩阵)。
推导:对恒等式
两边同时求导,再结合 |F| 的导数易得。
常见技巧及注意事项
实数在与一堆矩阵、向量作数乘时可以随意移动位置。且实数乘行向量时,向量数乘与矩阵乘法(1x1 矩阵和 1xm 矩阵相乘)的规则是一致的。
遇到相同下标求和就联想到矩阵乘法的定义,即
。特别地,一维下标求和联想到向量内积
,二维下标求和联想到迹
(A,B 应为同型矩阵)。
如果在一个求和式中,待求和项不是实数而是矩阵的乘积,不要想着展开求和式,而要按照上面的思路,看成分块矩阵的相乘!
向量的模长平方(或实数的平方和)转化为内积运算:
。矩阵的 F 范数的平方转化为迹运算:
。
多个矩阵相乘时,多用矩阵迹的求导公式转化、循环移动各项。实数也可看成 1X1 矩阵的迹!
需要用到向量(或矩阵)对矩阵求导的情形,要么把矩阵按列拆开转化成向量对向量求导(最终很有可能通过分块矩阵乘法再合并起来。本文后面的算例 PRML(3.33) 说明了这种方法怎么用),要么套用线性变换的求导公式(常见于神经网络的反向传播过程)。
算例
最小二乘法
方法一:展开括号,再使用几个常用公式化简即可:
方法二:使用线性变换的求导公式:
F 范数的求导公式推导
方法一:先转化为迹,再裂项,最后通过恰当的轮换,用迹方法的核心公式处理。
方法二:用线性变换的求导公式证。(注意矩阵转置不改变其 F 范数,并且实值函数对 X 和 X_T 的导数互为转置)
方法三:根据定义逐元素地算,然后合并成向量、再合并成矩阵。(太原始,易出错,不推荐)
PRML (3.33) 求导
题目:
求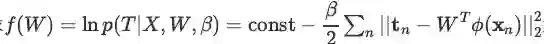
说明:上面的 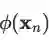
方法一:用矩阵的 F 范数推导:
上述几步的依据分别是:
将若干个列向量拼成一个矩阵,因此它们的二范数平方和就等于大矩阵的 F 范数的平方。
矩阵转置不改变其 F 范数。
矩阵数乘 (-1) 不改变其 F 范数。
线性变换的求导公式 + F 范数的求导公式。
实数在和矩阵作数乘时位置可以任意移动。
有了导数,再另导数等于零,即得 W 的最大似然解:
。
方法二: 将向量二范数用内积代替,然后逐项展开,最后利用分块矩阵相乘消掉求和号:
最后一步的化简的思考过程是把对 n 求和视为两个分块矩阵的乘积:
第一个矩阵是分块行向量,共 1xN 个块,且第 n 个分量是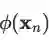
第二个矩阵是分块列向量,共 Nx1 个块,且第 n 个分量是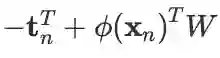
,注意第二个等号的推导过程中,前一项能够拆开是因为它被看做两个分块矩阵的乘积,两个分块矩阵分别由 Nx1和 1x1 个块组成。
这种方法虽然比较繁琐,但是更具有一般性。
RNN 的梯度消失爆炸问题
通常 RNN 的状态方程的更新定义为
(f 表示一个逐元素的激活函数,例如
等。),而这里我们采用 Pascanu 等人的论文 On the difficulty of training Recurrent Neural Networks 中的定义,即认为
(这两种方程其实是等价的,只是前一种表述把隐层状态定义成激活后的值,后一种表述把隐层状态定义成激活前的值,前述论文中的脚注里也有说明。这里采用后一种方式,是因为它稍微好算一点)。展开后的网络结构示意图参见 中的 Slide 15。以下内容建议对照这份讲义的 15-19 页一起观看(另注:建议用 Stanford 的讲义梳理大致的思路,但是按照本讲稿下述步骤进行具体的求导运算。个人认为本讲稿中的过程更加清楚)。
现在我们来计算损失函数 l 对循环连接的权重矩阵 W 的导数:假设每一时间步都有一个误差 l_t(例如建立一个语言模型,每一步都要预测下一个词的概率分布,与语料库里的真实值计算交叉熵),总的误差等于每一步的误差加起来:
,因此
(对一元函数来说,和的导数等于导数的和。根据多元函数偏导数的定义,很容易推广到多元函数上,进而推广到矩阵求导上)。
考虑到矩阵 W 出现了多次,计算
需要计算 l_t 对 W 的每一次出现的导数,然后再求和。若用 W^(k) 表示 h_k-1 与 h_k之间的转移矩阵 W,则
。其中第二个等号用到的是线性变换的求导公式(类似标准 BP 算法的核心步骤)
然后根据雅克比矩阵的运算规则计算损失函数对隐层的导数
(表示将括号里的向量变成一个对角矩阵,跟前文的
互为逆运算。):
,再将该式带入上一步中的式子,就得到
,这就是 vanilla RNN 的 BPTT 的公式。(中间很多个隐层之间的雅克比相乘那一部分可以用求积符号来书写,这里的写法更直观一些)
注:实践中具体计算梯度的时候,一般还是先定义一组类似于 BP 神经网络 δ_t 的变量,使用循环逐层进行求导,而不是强行直接展开。这里展开是为了理论分析方便。
另注:Stanford 的讲义和前述论文中,均认为
,这一点应该是错的,矩阵 W 不应该被转置,根据雅克比矩阵的定义写一个梯度检查的程序即可快速验证这一点。
Autoencoder with Tied-weight
求函数
对 W 的导数,其中
是逐元素求 Sigmoid。
根据变量多次出现的求导法则计算即可:
,其中 W_c 的含义是将 W 此次出现看做常数。
上式右边第一项计算如下:
第二项计算如下:
,其中第三个等号里定义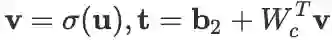
最终结果就是将以上两项合并起来,并去掉所有 W_c 中的下标,从略。
本文最先由七月发表于知乎专栏:https://zhuanlan.zhihu.com/p/25063314

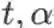
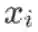
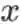
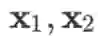
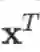
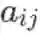
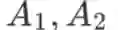
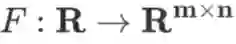
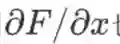
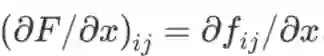
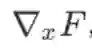
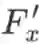
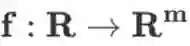
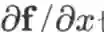
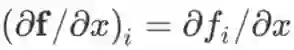
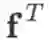
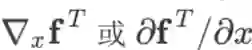
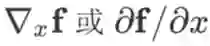
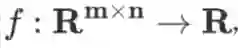
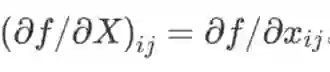
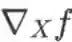
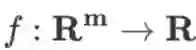
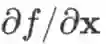
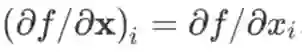
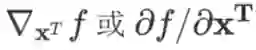
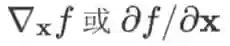
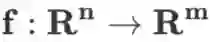
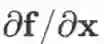
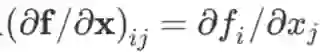
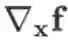
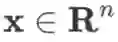
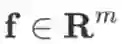
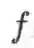
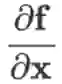
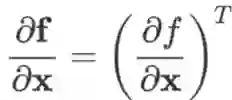

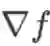
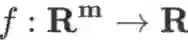
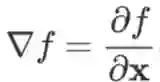
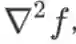
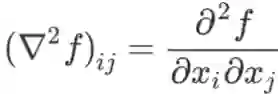
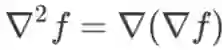
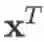
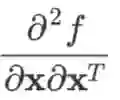
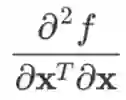
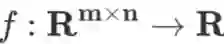
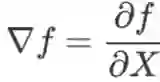
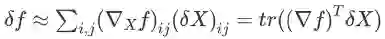
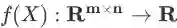
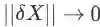
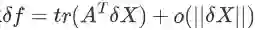
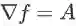
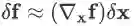

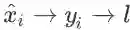
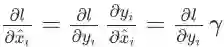
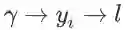
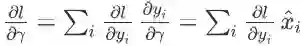
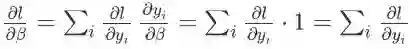
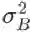
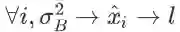
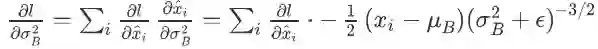
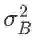
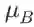
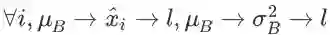
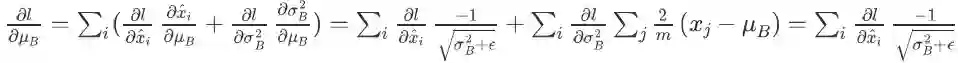
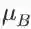
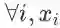
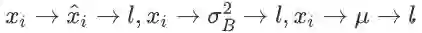
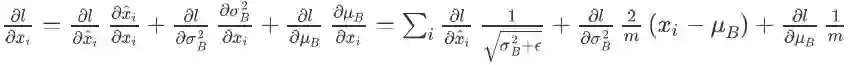
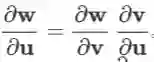
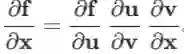
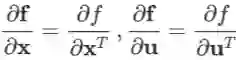
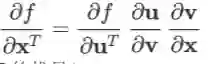
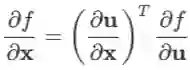
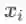
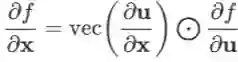
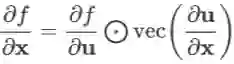
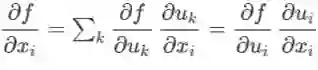
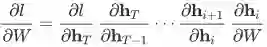
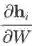
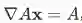
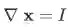
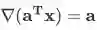
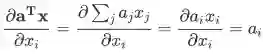
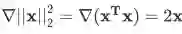
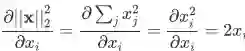
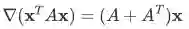
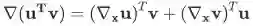
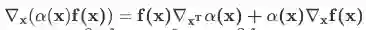
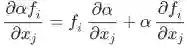
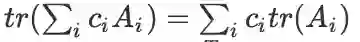
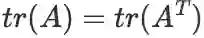
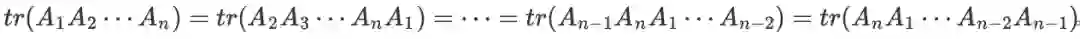
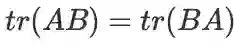
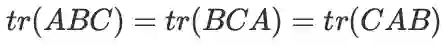
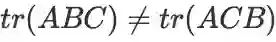
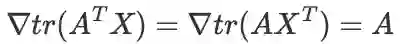
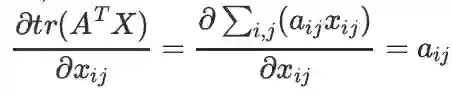
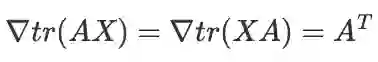
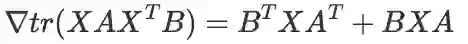
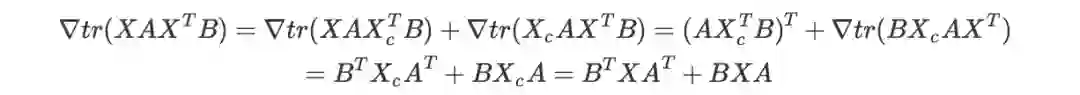
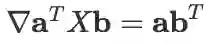
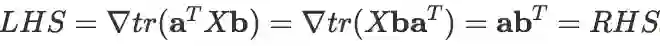
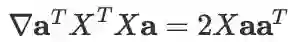
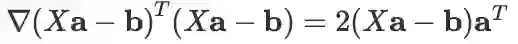
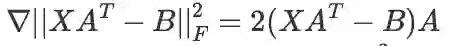
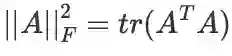 即可。特别地,
即可。特别地,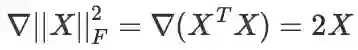 (此式也可逐元素求导直接验证)
(此式也可逐元素求导直接验证)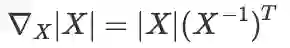
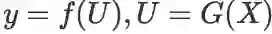 ,则:
,则: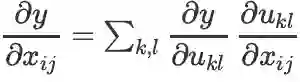 ,或简写为
,或简写为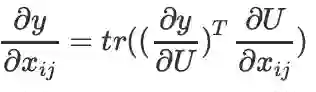
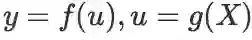 ,则:
,则: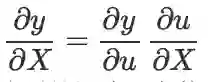 (等式右边是实数和矩阵的数乘)
(等式右边是实数和矩阵的数乘)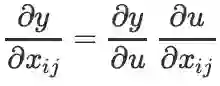
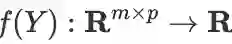 及线性映射
及线性映射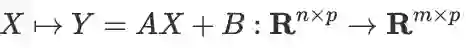 (因此
(因此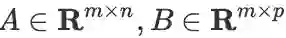 ),则:
),则: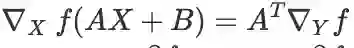
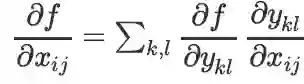 ,而
,而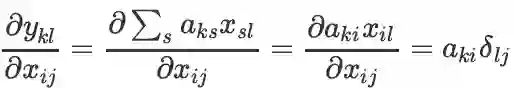 (
(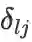 是 Kronecker delta 符号:若l=j 值为 1,否则为 0),将后式代入前式,得:
是 Kronecker delta 符号:若l=j 值为 1,否则为 0),将后式代入前式,得: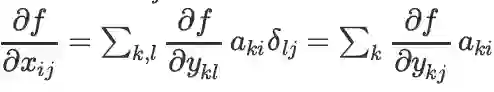
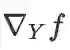
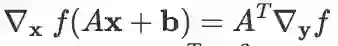
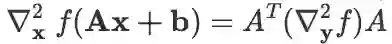
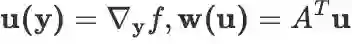 ,则
,则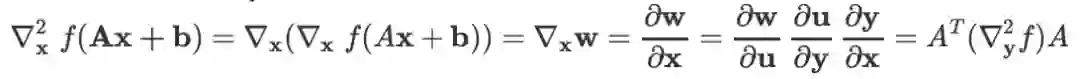
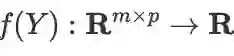 及线性映射
及线性映射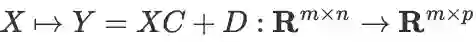 (因此
(因此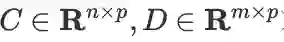 ),则:
),则: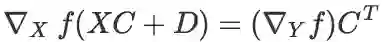
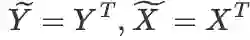 ,则变量依赖关系变为:
,则变量依赖关系变为: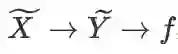 ,且
,且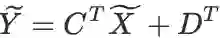 ,根据线性变换的求导法则,知:
,根据线性变换的求导法则,知: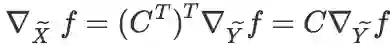
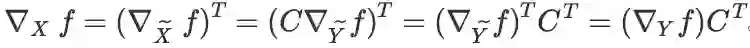
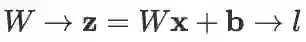 的依赖关系。其中 x 是神经网络某一层的输入数据(不是训练神经网络时要求导的变量!不过在构造对抗样本时可能需要对 x 求导), W,b 是该层的参数(这才是训练神经网络时要求导的变量),z 是经过变换后预备输入给下一层的值,l 是最终的损失函数。根据上述线性变换的求导公式,立即可以得到 BP 算法的核心步骤:
的依赖关系。其中 x 是神经网络某一层的输入数据(不是训练神经网络时要求导的变量!不过在构造对抗样本时可能需要对 x 求导), W,b 是该层的参数(这才是训练神经网络时要求导的变量),z 是经过变换后预备输入给下一层的值,l 是最终的损失函数。根据上述线性变换的求导公式,立即可以得到 BP 算法的核心步骤: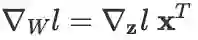
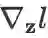 定义为变量
定义为变量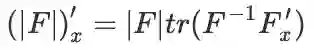
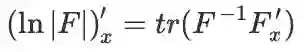
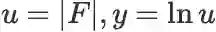 ,则:
,则: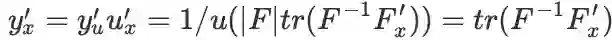 。
。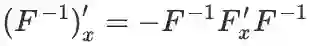
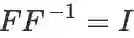 两边同时求导,再结合 |F| 的导数易得。
两边同时求导,再结合 |F| 的导数易得。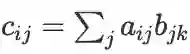 。特别地,一维下标求和联想到向量内积
。特别地,一维下标求和联想到向量内积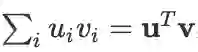 ,二维下标求和联想到迹
,二维下标求和联想到迹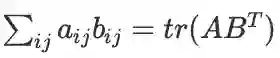 (A,B 应为同型矩阵)。
(A,B 应为同型矩阵)。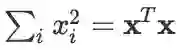 。矩阵的 F 范数的平方转化为迹运算:
。矩阵的 F 范数的平方转化为迹运算: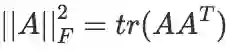 。
。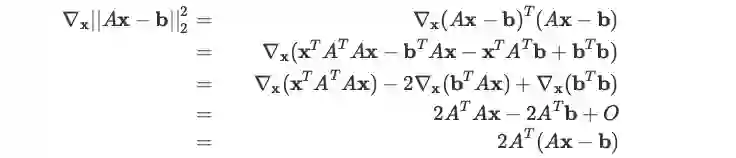
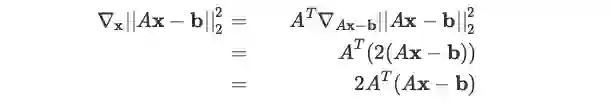
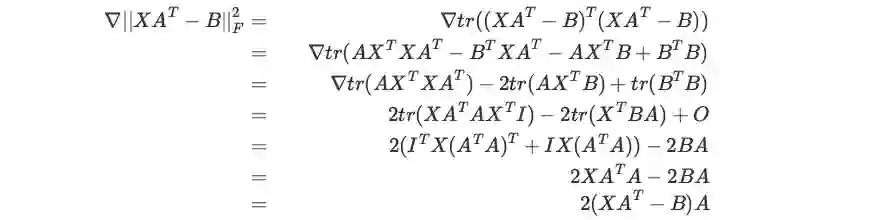
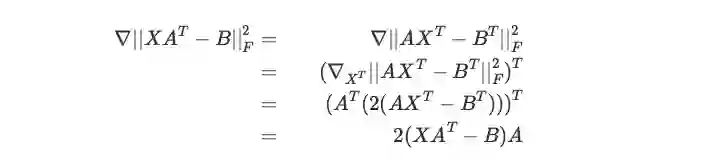
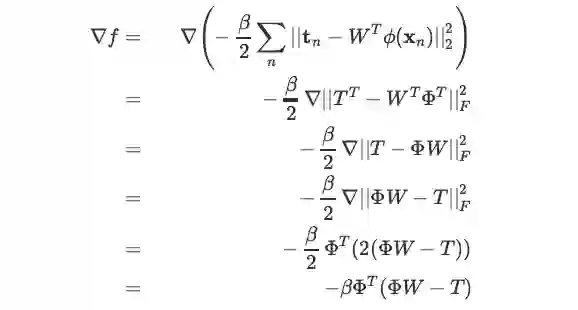
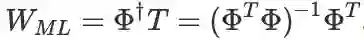 。
。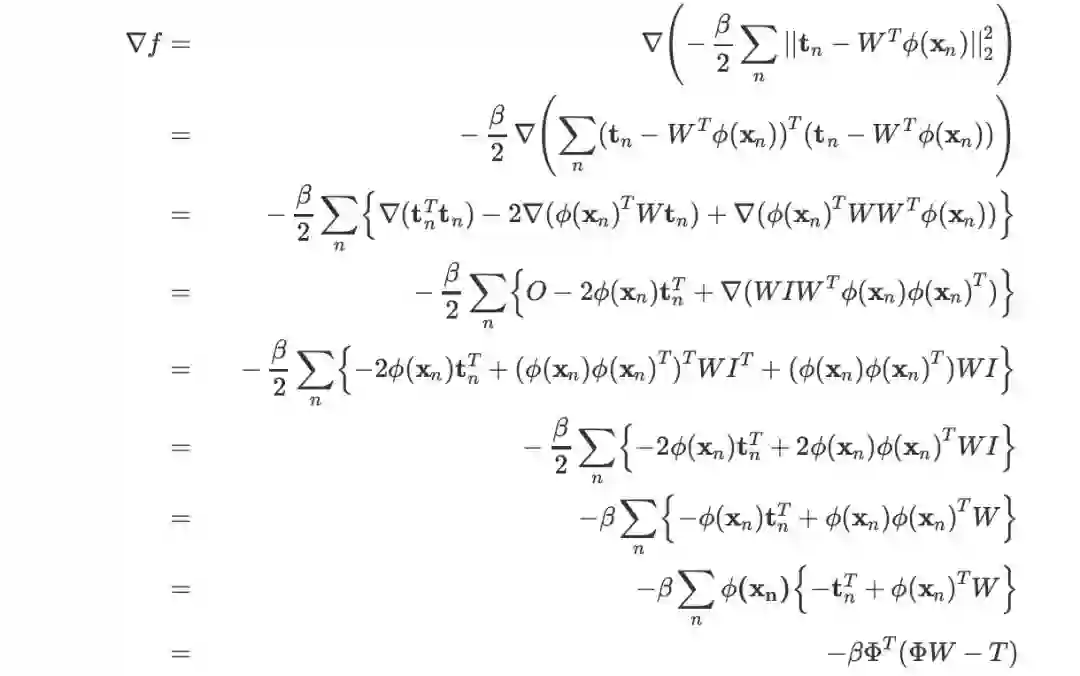
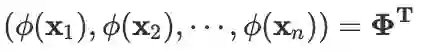
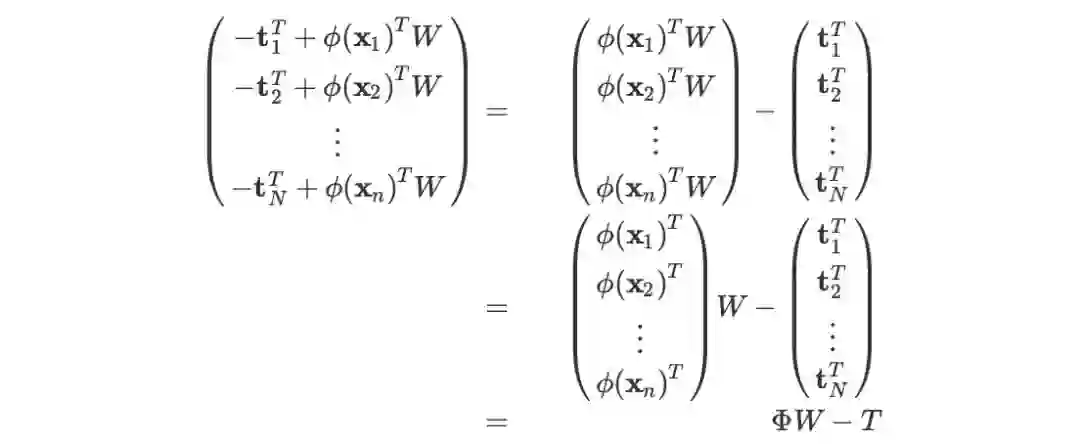
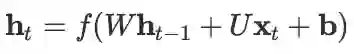 (f 表示一个逐元素的激活函数,例如
(f 表示一个逐元素的激活函数,例如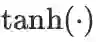 等。),而这里我们采用 Pascanu 等人的论文 On the difficulty of training Recurrent Neural Networks 中的定义,即认为
等。),而这里我们采用 Pascanu 等人的论文 On the difficulty of training Recurrent Neural Networks 中的定义,即认为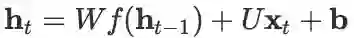 (这两种方程其实是等价的,只是前一种表述把隐层状态定义成激活后的值,后一种表述把隐层状态定义成激活前的值,前述论文中的脚注里也有说明。这里采用后一种方式,是因为它稍微好算一点)。展开后的网络结构示意图参见 中的 Slide 15。以下内容建议对照这份讲义的 15-19 页一起观看(另注:建议用 Stanford 的讲义梳理大致的思路,但是按照本讲稿下述步骤进行具体的求导运算。个人认为本讲稿中的过程更加清楚)。
(这两种方程其实是等价的,只是前一种表述把隐层状态定义成激活后的值,后一种表述把隐层状态定义成激活前的值,前述论文中的脚注里也有说明。这里采用后一种方式,是因为它稍微好算一点)。展开后的网络结构示意图参见 中的 Slide 15。以下内容建议对照这份讲义的 15-19 页一起观看(另注:建议用 Stanford 的讲义梳理大致的思路,但是按照本讲稿下述步骤进行具体的求导运算。个人认为本讲稿中的过程更加清楚)。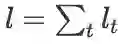 ,因此
,因此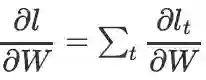 (对一元函数来说,和的导数等于导数的和。根据多元函数偏导数的定义,很容易推广到多元函数上,进而推广到矩阵求导上)。
(对一元函数来说,和的导数等于导数的和。根据多元函数偏导数的定义,很容易推广到多元函数上,进而推广到矩阵求导上)。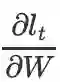 需要计算 l_t 对 W 的每一次出现的导数,然后再求和。若用 W^(k) 表示 h_k-1 与 h_k之间的转移矩阵 W,则
需要计算 l_t 对 W 的每一次出现的导数,然后再求和。若用 W^(k) 表示 h_k-1 与 h_k之间的转移矩阵 W,则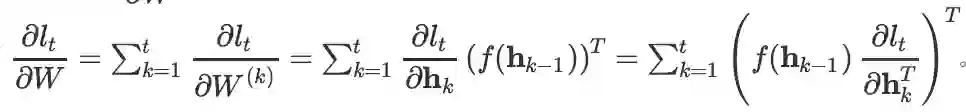 。其中第二个等号用到的是线性变换的求导公式(类似标准 BP 算法的核心步骤)
。其中第二个等号用到的是线性变换的求导公式(类似标准 BP 算法的核心步骤)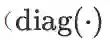 (表示将括号里的向量变成一个对角矩阵,跟前文的
(表示将括号里的向量变成一个对角矩阵,跟前文的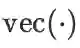 互为逆运算。):
互为逆运算。):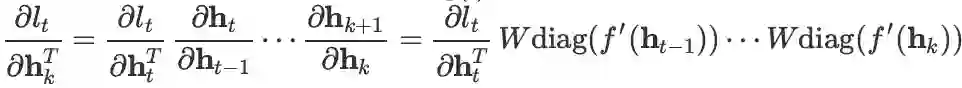 ,再将该式带入上一步中的式子,就得到
,再将该式带入上一步中的式子,就得到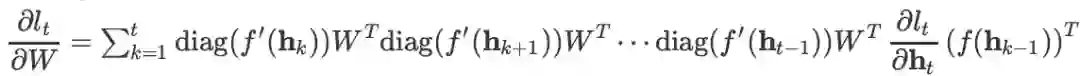
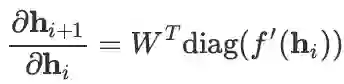 ,这一点应该是错的,矩阵 W 不应该被转置,根据雅克比矩阵的定义写一个梯度检查的程序即可快速验证这一点。
,这一点应该是错的,矩阵 W 不应该被转置,根据雅克比矩阵的定义写一个梯度检查的程序即可快速验证这一点。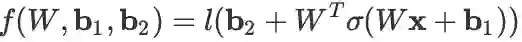 对 W 的导数,其中
对 W 的导数,其中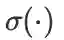 是逐元素求 Sigmoid。
是逐元素求 Sigmoid。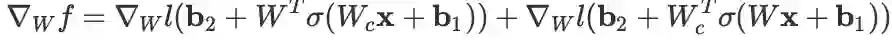 ,其中 W_c 的含义是将 W 此次出现看做常数。
,其中 W_c 的含义是将 W 此次出现看做常数。