消失的梯度问题：问题，原因，意义及其解决对策

2019 年 6 月 12 日 AI研习社

本文为 AI 研习社编译的技术博客，原标题：

The Vanishing Gradient Problem

作者 | Chi-Feng Wang

翻译 | Dddda 编辑 | 王立鱼

原文链接：

https://towardsdatascience.com/solving-nlp-task-using-sequence2sequence-model-from-zero-to-hero-c193c1bd03d1

注：本文的相关链接请访问文末【阅读原文】

问题

随着越来越多的激活函数加到神经网络中，损失函数的梯度趋近于0，使得网络结构很难训练。

原因

具体的激活函数，比如sigmoid函数，把很大的空间压缩到0和1之间。因此，sigmoid函数的输入即使变化很大也只会改变一点输出。因此，求导就变得很小。

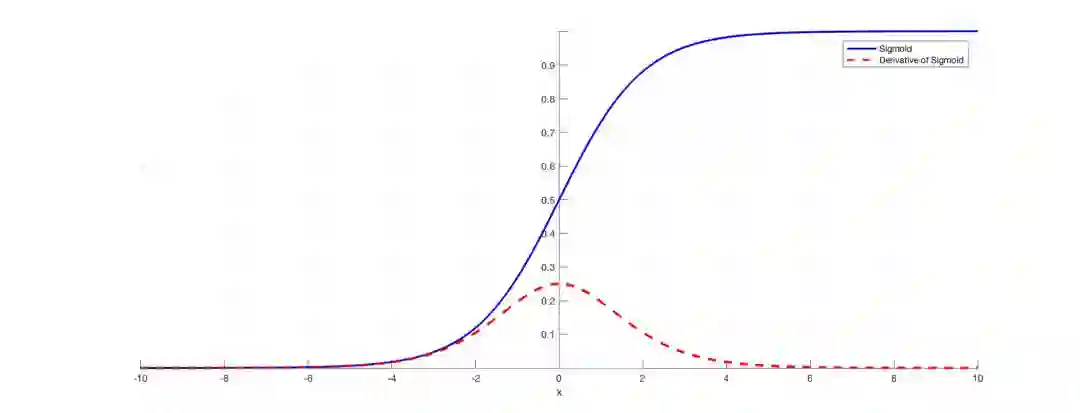
图1：sigmoid函数以及导数

例如，图一是sigmoid函数及其导数。注意当sigmoid函数的输入变大或变小时（当|x|），导数如何接近零。

为什么这是重要的?

对于使用激活函数的仅有几层的浅层网络结构，这不是很大的问题。然而，当使用更多层的时候，可能会造成梯度太小而不能很好的训练。

神经网络的梯度是使用反向传播来找到的。简单来说，反向传播通过将网络从最终层逐层移动到初始层来找到网络的导数。通过链式的规则，将各层的导数乘上网络（从最终层到初始层），计算出初始层的导数。

然而，当有n个隐藏层使用像sigmoid的激活函数时，n个小的倒数相乘。因此，当我们反向传到初始层的时候，梯度会大幅度下降。

一个小的梯度意味着初始层的权重和偏差不会在训练中得到有效更新。由于这些初始层通常对识别输入数据的核心元素至关重要，因此可能导致整个网络的整体不准确。

解决方案

最简单的解决方案是使用激活函数，像ReLU，不会导致一个小的导数。

残差网络是另外一个解决方案，因为提供了残差与之前的层直接连接。就像图2中，残差连接直接将block的开头x的值添加到block（F(x)+x）的结尾。

这个残差连接不通过“挤压”的激活函数，从而导致block的整体倒数更大。

图2：残差层

*************************************************************************

译者个人注解：精髓就在于直接连过来的那个x了。h（x）＝f（x）＋ x，h（x）对 x 求偏导，值为1，这个1直接传到block的最前端，保证了来自后一层的梯度值完好的传过了这一层然后进入到前一层，使得浅层的weights也可以得到很好的训练。

*************************************************************************

最后，batch normalization层还可以解决这个问题。如前所述，当一个大的输入空间映射到一个小的输入空间时，问题就出现了，导致导数消失。在图1中，很清晰看到|x|变大的时候。bath normalization通过简单地规范化输入来减少这个问题，这样x就不会到达sigmoid函数的外边缘。如图3所示，它对输入进行了规范化，使其大部分落在绿色区域，其中导数不太小。

图三：限制输入的sigmoid 函数

如果你有任何的问题或者建议，记得评论 :）

阅读以下的文章来获得更多的信息：

https://www.quora.com/What-is-the-vanishing-gradient-problem
https://en.wikipedia.org/wiki/Vanishing_gradient_problem
https://towardsdatascience.com/intuit-and-implement-batch-normalization-c05480333c5b

想要继续查看该篇文章相关链接和参考文献？

点击底部【阅读原文】即可访问：

https://ai.yanxishe.com/page/TextTranslation/1739

注：上周的赠书活动，由于小编端午节给自己多放了一天假，因此留言还在筛选中，明天公布中奖名单，敬请谅解哈。

滑动查看更多内容