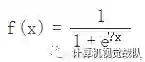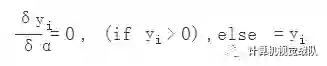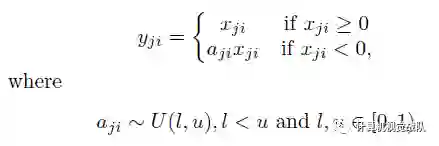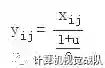最近流行的激活函数

最近又看了点深度学习的东西，主要看了一些关于激活函数的内容，不知道算不算新颖，但是我想把自己阅读后的分享一下，请各位给予评价与指点，谢谢！

一般激活函数有如下一些性质：

1. 非线性： 
   当激活函数是线性的，一个两层的神经网络就可以基本上逼近所有的函数。但如果激活函数是恒等激活函数的时候，即f(x)=x，就不满足这个性质，而且如果MLP使用的是恒等激活函数，那么其实整个网络跟单层神经网络是等价的；

2. 可微性： 
   当优化方法是基于梯度的时候，就体现了该性质；

3. 单调性： 
   当激活函数是单调的时候，单层网络能够保证是凸函数；

4. f(x)≈x： 
   当激活函数满足这个性质的时候，如果参数的初始化是随机的较小值，那么神经网络的训练将会很高效；如果不满足这个性质，那么就需要详细地去设置初始值；

5. 输出值的范围： 
   当激活函数输出值是有限的时候，基于梯度的优化方法会更加稳定，因为特征的表示受有限权值的影响更显著；当激活函数的输出是无限的时候，模型的训练会更加高效，不过在这种情况小，一般需要更小的Learning Rate。

Sigmoid

常用的非线性的激活函数，数学形式如下： 

Sigmoid 函数曾经被使用的很多，不过近年来，用它的人越来越少了。主要是因为它的缺点（输入较大或较小的时候，最后梯度会接近于0），最终导致网络学习困难。

所以，出现了另一种激活函数：ReLU 

ReLU

f(x)=max(0,x)

优点： 

使用 ReLU得到的SGD的收敛速度会比 sigmoid/tanh 快。这是因为它是linear，而且ReLU只需要一个阈值就可以得到激活值，不用去计算复杂的运算。

缺点： 

训练过程该函数不适应较大梯度输入，因为在参数更新以后，ReLU的神经元不会再有激活的功能，导致梯度永远都是零。

为了针对以上的缺点，又出现Leaky-ReLU、P-ReLU、R-ReLU三种拓展激活函数。

Leaky ReLUs 
该函数用来解决ReLU的缺点，不同的是：

                         f(x)=αx，(x<0)                         f(x)=x，(x>=0)

这里的 α 是一个很小的常数。这样，即修正了数据分布，又保留了一些负轴的值，使得负轴信息不会全部丢失。

Parametric ReLU 

对于 Leaky ReLU 中的α，通常都是通过先验知识人工赋值，可以观察到损失函数对α的导数是可以求得的，可以将它作为一个参数进行训练。

《Delving Deep into Rectifiers: Surpassing Human-Level Performance on 
ImageNet Classification》

该文章指出其不仅可以训练，而且效果特别好。公式非常简单，其中对α的导数：

原文使用了Parametric ReLU后，最终效果比不用提高了1.03%。

Randomized ReLU

Randomized Leaky ReLU 是 Leaky ReLU 的随机版本（α 是随机选取）。 它首次是在NDSB 比赛中被提出。

核心思想就是，在训练过程中，α是从一个高斯分布U(l,u)中随机出来的，然后再测试过程中进行修正（与Dropout的用法相似）。

数学表示如下： 

在测试阶段，把训练过程中所有的αji取个平均值。NDSB冠军的α是从 U(3,8) 中随机出来的。在测试阶段，激活函数如下：

---

ReLU深度网络能逼近任意函数的原因

很早前就读了一遍谷歌大脑工程师Eric Jang的一个解答，想把这个知识与大家分享！最近也发现，有很多牛人喜欢在博客中分享DL的相关知识，所以个人感觉有空可以在博客中度阅读一些相关内容，对自己基础和深度了解有很大的帮助，也在此感谢那些为DL&ML默默共享的大牛们，让我们一起努力学习！！！那就不多说了，开始对这个话题的理解。嘿嘿！

有很多人问：为什么ReLU深度网络能逼近任意函数？

对此，其有深入见解，但是在此他是简单，并用最少的数学形式来解释这个问题。ReLU其实是分段线性的，所以有人会质疑，对于一个固定大小的神经网络，ReLU网络可能不具有更平滑+有界的激活函数（如tanh）的表达。

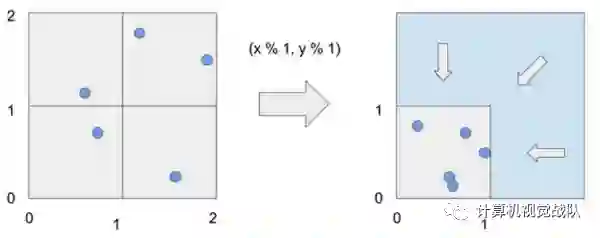
因为他们学习非平滑函数，ReLU网络应该被解释为以分段线性方式分离数据，而不是实际上是一个“真实”函数近似。 在机器学习中，人们经常试图从有限离散数据点（即100K图像）的数据集中学习，并且在这些情况下，只需学习这些数据点的分隔就足够了。考虑二维模数运算符，即：

vec2 p = vec2(x,y) // x,y are floats     vec2 mod(p,1) {     return vec2(p.x % 1, p.y % 1)    }

mod函数的输出是将所有2D空间折叠/散架到单位平方上的结果。 这是分段线性，但高度非线性（因为有无限数量的线性部分）。

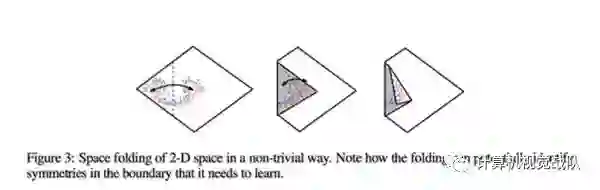
用ReLU激活的深层神经网络工作相似-它们将激活空间分割/折叠成一簇不同的线性区域，像一个真正复杂的折纸。

可以看“On the number of linear regions of Deep Neural Networks”这篇文章的第三幅图，就很清楚表现了。

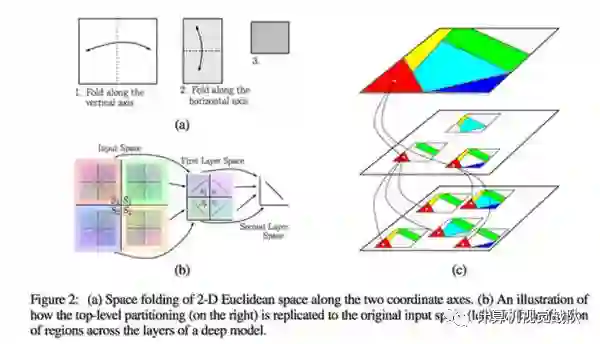
在文章的图2中，它们展示了在网络中层的深度/层数的如何增加的，线性区域的数量呈指数增长。 

事实证明，有足够的层，你可以近似“平滑”任何函数到任意程度。 此外，如果你在最后一层添加一个平滑的激活函数，你会得到一个平滑的函数近似。

一般来说，我们不想要一个非常平滑的函数近似，它可以精确匹配每个数据点，并且过拟合数据集，而不是学习一个在测试集上可正常工作的可泛化表示。 通过学习分离器，我们得到更好的泛化性，因此ReLU网络在这种意义上更好地自正则化。

详情：A Comparison of the Computational Power of Sigmoid and Boolean Threshold Circuits