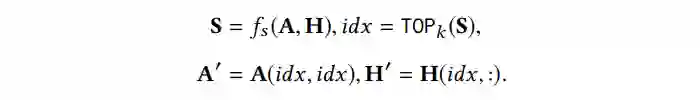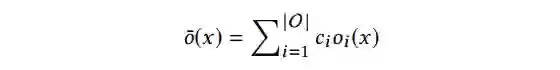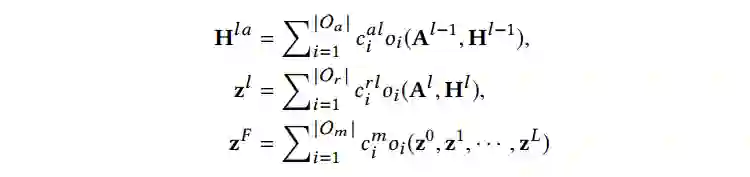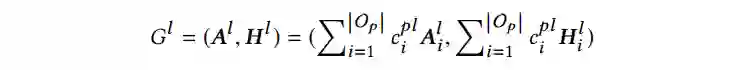CIKM'21 | 基于池化结构搜索的图分类

会员服务 ·

CIKM'21 | 基于池化结构搜索的图分类

2021 年 11 月 9 日 图与推荐

论文标题：

Pooling Architecture Search for Graph Classification

论文地址：

https://arxiv.org/abs/2108.10587

代码地址：

https://github.com/AutoML-Research/PAS

备注：该论文已经被数据挖掘会议 CIKM 2021 接收，欢迎大家关注。如有任何问题，欢迎联系 weilanning@ict.ac.cn。

简介

近年来 GNN（Graph Neural Network）成为工业界和学术界非常热门的一个研究方向。在图分类任务中，不同的池化操作应用在了 graph-level 的特征学习中。但是面对多样的数据集和任务，没有任何一个方法能够稳定取得 SOTA 效果。最近，斯坦福大学 Jure 教授团队在 NeurIPS 2020 的工作上也指出了这一点 [1] 。

基于此，我们结合自动化机器学习（AutoML） [2-5] 来获取任务自适应的池化图神经网络。具体来说，我们提出了一个基于图分类任务的统一框架，并在此基础上设计了新的搜索空间（search space）。为效率起见，我们提出了一个 coarsening strategy 来解决池化操作的松弛问题，从而可微搜索算法（differentiable search algorithm）可以被应用到池化结构搜索中。我们的池化结构搜索方法（Pooling Architecture Search，简记为 PAS）能够在取得 SOTA 表现的同时还十分高效。

背景介绍

图分类任务有大量的应用场景，比如蛋白质/化学分子性质预测 [6] ，社交网络分析 [7]，文档分类 [8] 等，如图 1 所示。

▲ 图1：图分类的应用场景示例

相比较于 node-level 的任务，图分类任务需要学习 graph-level 的特征表示，池化操作也由此被提出。一个简单直接的方案就是取所有节点的的特征均值或者和，这类操作被称为全局池化操作（global pooling）；这类操作学到的是单层次的 graph-level 特征，无法捕获图结构中的层次化信息。层次化的池化（hierarchical pooling）方案就是为了解决这个问题，它通过生成越来越粗粒度的图来提取层次化的 graph-level 信息。

现有的图分类方案提供了不同的 global 和 hierarchical 的池化方案，比如 DGCNN [10] ，DiffPool [11] ，SAGPool [12] ，ASAP [13] ，Graph U-Net [14] 等。现有的 GNN 结合神经网络结构搜索（neural architecture search，简记为NAS）的方案，都是专注于 node-level 的工作，比如 GraphNAS [15]， SNAG [16] ，SANE [17] 等，缺少 graph-level 的探索，方案 [18] 考虑了 global pooling 的设计，但是它基于演化算法（Evolutionary algorithm，简记为 EA），耗时长效率低。这些方案缺少了对池化结构的重要部分的探索，即缺少对 hierarchical pooling 的设计。基于上述，如何能快速高效的设计数据自适应的图分类任务 GNN 是一个大的挑战。

本次工作的方法

为了解决上述的问题，我们提出了新的解决方案 PAS（Pooling architecture search），其中包括一个统一框架，基于该框架的设计的搜索空间，以及考虑到效率而设计的 coarsening strategy。

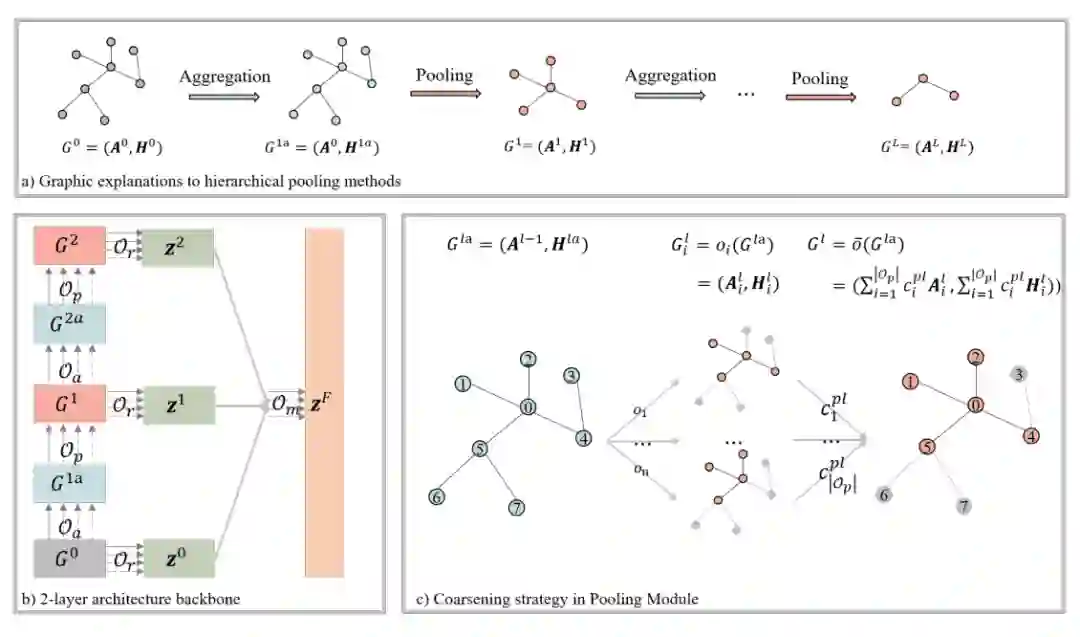
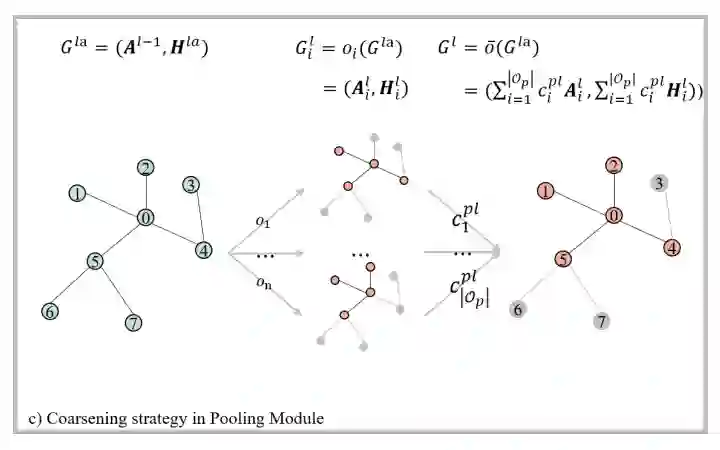
从现有的图分类 GNN 中，我们提取了四个重要的模块，聚合模块（Aggregation Module），池化模块（Pooling Module），读出模块（Readout Module）和融合模块（Merge Module）。以图 1（b）的两层结构为例，针对输入的图，聚合模块更新了节点自身信息，结果可以表示为，随后池化模块产生粗粒度的图。

这两个操作的示意图展示在（a）中，第二层的聚合模块和池化模块也是同样的操作。三个读出模块用来读出每一层的 graph-level 特征，最后聚合模块基于生成的特征生成最终的 graph-level 特征。

▲ 图2：PAS方案示意图

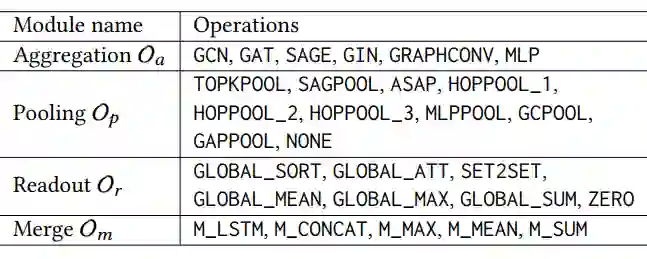
基于这个统一框架，我们提出了一个 NAS 方案来搜索池化结构。按照 NAS 的一贯设计，我们给出了搜索空间中各个模块的操作集合，如表 1 所示。

▲ 表1：搜索空间

在本文中，池化操作的过程可以被统一为如下公式。其中存储着节点的得分，由打分函数得到，之后函数选择出分数排名前的节点。粗粒度图的邻接矩阵和节点特征矩阵可以按照对应公式采样得到。基于这个公式，我们提供了 10 种池化操作，详情请见论文。

可微搜索算法中，一项重要的设计就是松弛函数。如下所示，离散空间可以被松弛为连续空间，其中是集合中第个操作的权重。

基于这个松弛函数，聚合模块、读出模块和融合模块的结果可以按照如下公式计算。

但是这对池化操作来说是不可实现的，如下图所示，池化操作和产生了不同的节点集合和，此时粗粒度图中的特征矩阵都是，虽然具有相同的矩阵大小，但是因为节点集合不匹配所以无法直接加权求和。

我们设计了新的 coarsening strategy 来解决这个问题，在产生了候选的个节点后，那些没有选中部分记为 0。也就是说，下图中未被选中的节点（灰色节点）特征为 0，未被选中的边（灰色的边）权重为 0。当前策略下生成的粗粒度图，具有和输入图一样的“形状”，因此池化模块的结果可以按照下述公式计算。

▲ 图3：池化模块

在设计的 coarsening strategy 基础上，整个框架可以用梯度下降来优化。搜索完成后，取出每个模块中权重最大的操作，基于此我们可以得到搜索的池化结构。

实验

该工作在六个常用的图分类数据集上做了验证。

4.1 PAS的实验效果

▲ 表2：实验效果对比

▲ 图4：不同数据集上搜索的GNN结构

▲ 图5：准确率和模型参数的对比

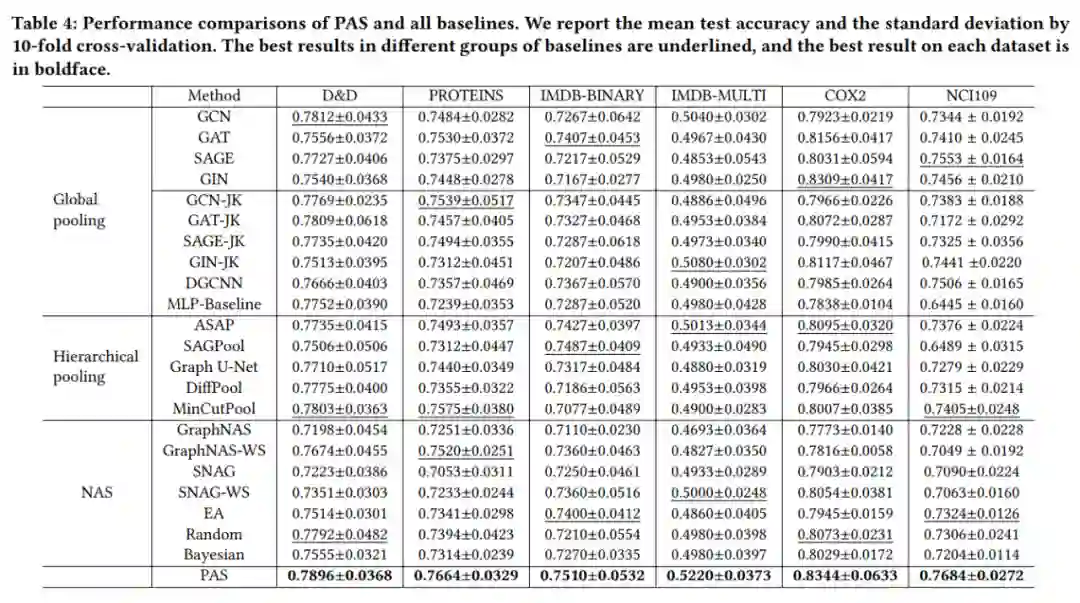
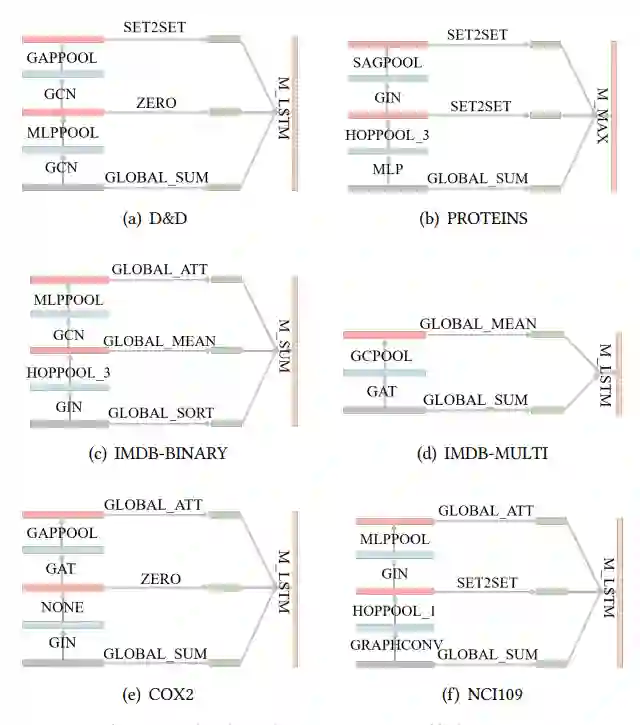
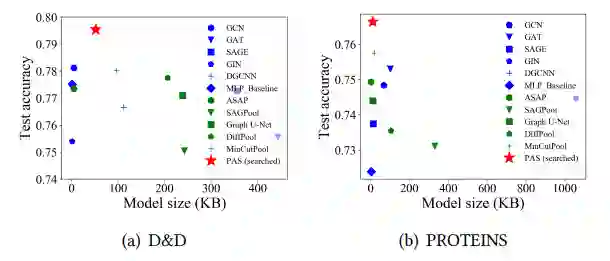
如表 2 所示，PAS 比现有的两类池化方案和 NAS 方案的效果更好，这也体现了我们提出的方案的有效性。搜索出的 GNN 结构如图 4 所示，不同数据集上的结构各不相同，并且在 COX2 数据集上，搜索的 GNN 退化为一个 global pooling 的方案。图 5 中展示了测试集上准确率和模型参数的对比，PAS 搜索出来的结构能够用更少的参数获得更高的结果。综合这些实验结果，PAS 的效率和效果是显而易见的。

4.2 消融实验（Ablation Study）

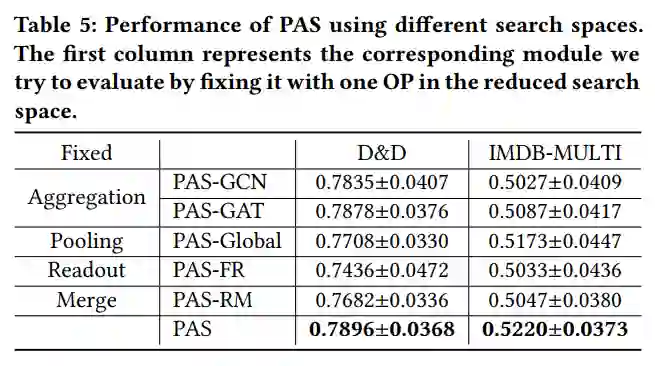
针对 PAS 的四个模块，我们设计了对应的消融实验来验证四个模块的重要性。如表 3 所示，这些方案的效果低于 PA 本身，这展示了我们设计的统一框架的有效性。

▲ 表3：消融实验中的效果对比

4.3 效率对比

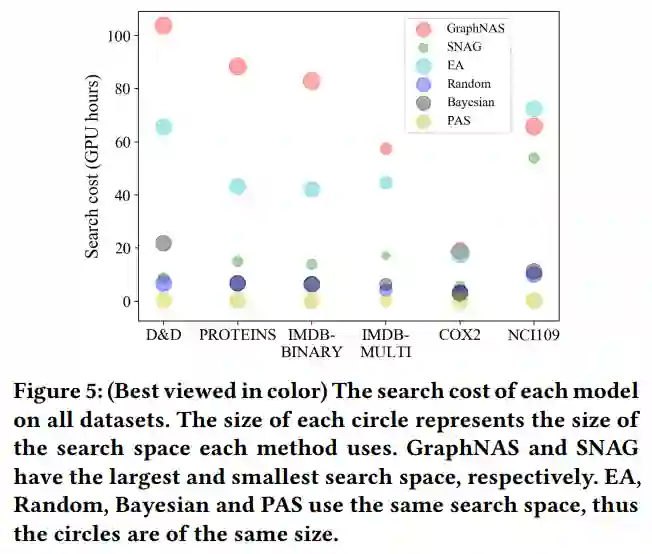
如下图所示，我们对比了不同方案的搜索空间大小和搜索耗时。圆圈大小代表了搜索空间的大小，不同颜色代表了不同方案。PAS 的搜索空间大小介于 GraphNAS 和 SNAG 之间，但是具有最小的搜索耗时和最高的效果。结合图 5，PAS 的高效性显而易见。

▲ 图6：搜索耗时和搜索空间的对比

结论

本文提出了一种自动设计池化结构的方案 PAS。PAS 中包含一个新的统一框架，它由四个常用的模块组成。在此基础上，我们提供了对应的搜索空间并设计了 coarsening strategy 来松弛这个搜索空间。基于此，可微搜索这种高效的搜索算法能被应用到池化结构搜索中。我们设计了充分的实验来验证搜索空间和搜索算法这两部分，结果显示 PAS 比现有的方案结果更好效率更高。

本组其他相关工作

本文探索了 NAS 在图分类任务中的应用，除此之外，本组还有以下新工作：

AutoSF: Searching scoring functions for knowledge graph embedding. ICDE 2020. (AutoSF)
Interstellar: Searching Recurrent Architecture for Knowledge Graph Embedding. NeurIPS 2020. (Interstellar)
Search to aggregate neighborhood for graph neural network. ICDE 2021. (SANE)
Simplifying Architecture Search for Graph Neural Network. CIKM-CSSA 2020 (SNAG)
Searching to Sparsify Tensor Decomposition for N-ary relational data. WWW 2021. (S2S)
DiffMG: Differentiable Meta Graph Search for Heterogeneous Graph Neural Networks. KDD 2021. (DiffMG)
TabGNN: Multiplex Graph Neural Network for Tabular Data Prediction. KDD-DLP 2021. (TabGNN)