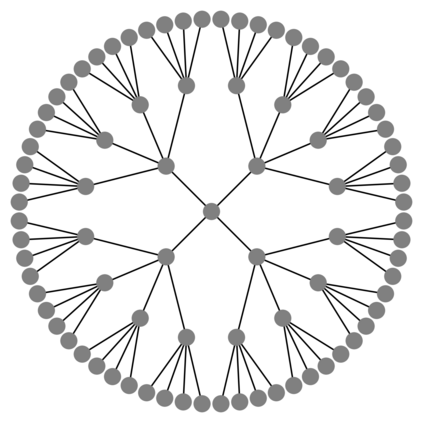
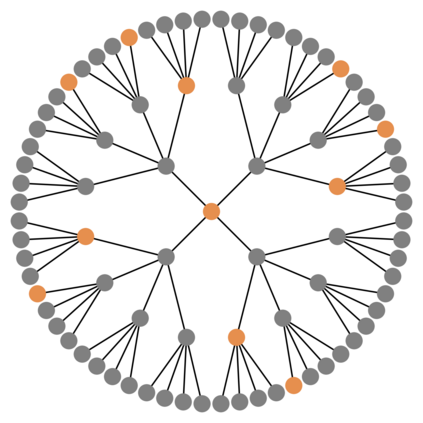
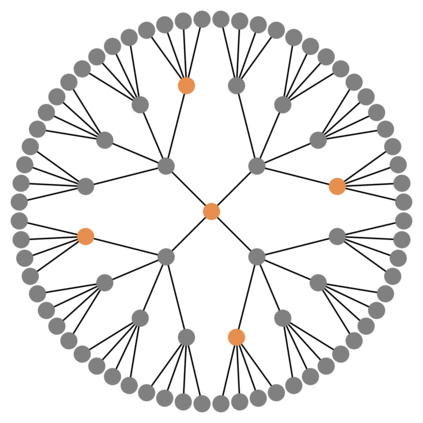
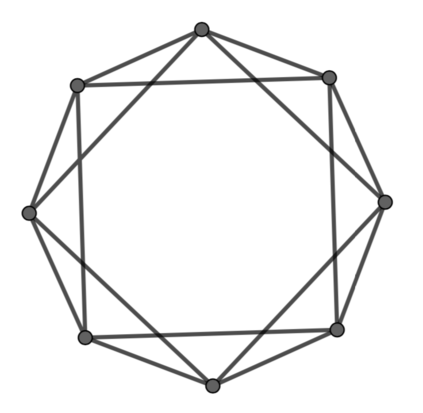
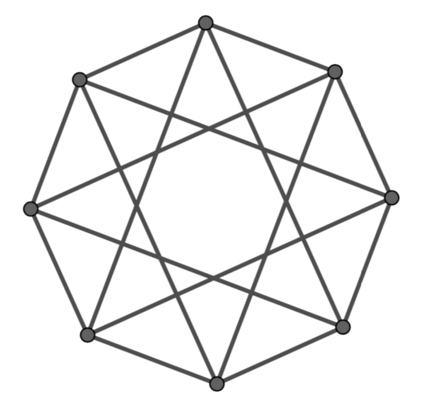
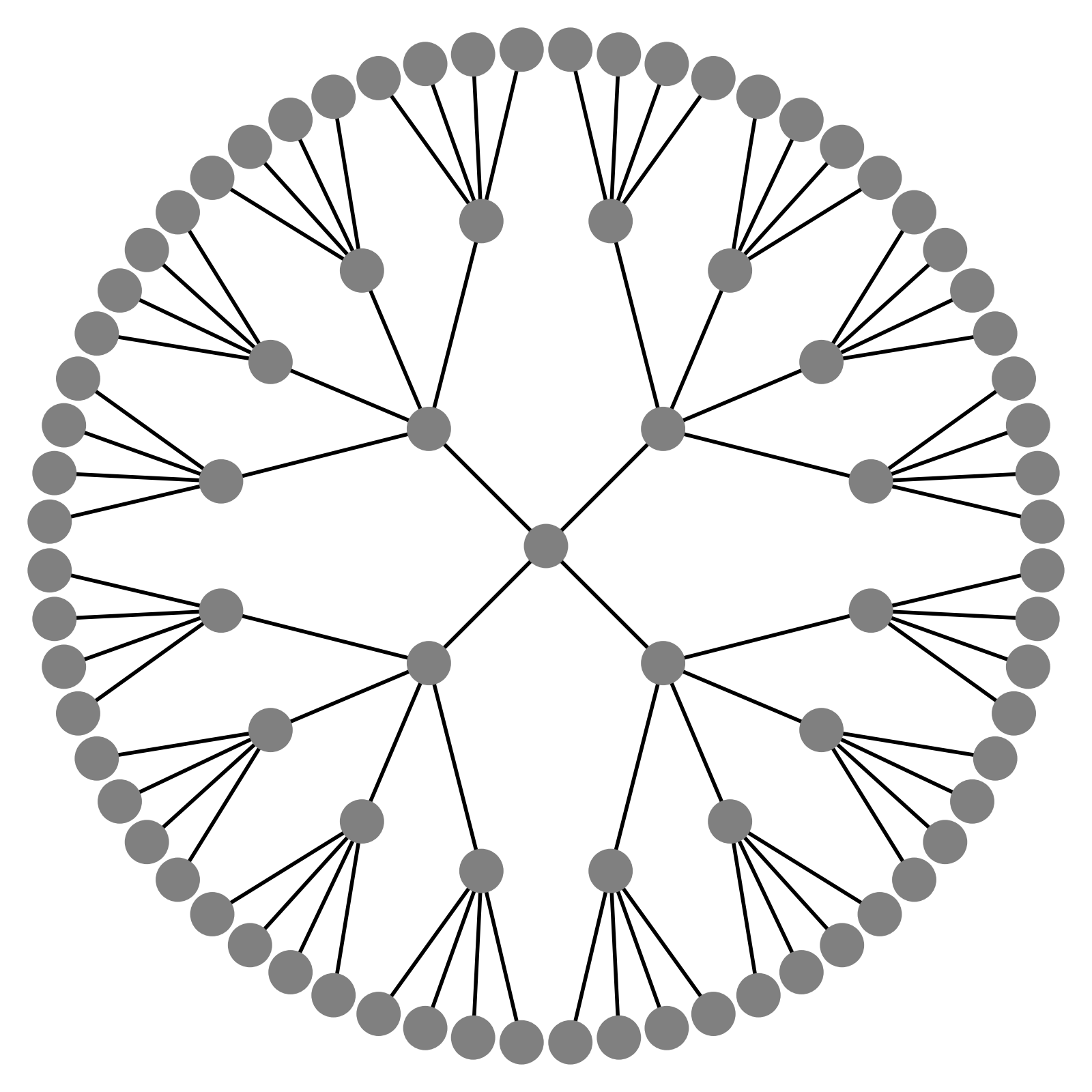
Message passing Graph Neural Networks (GNNs) provide a powerful modeling framework for relational data. However, the expressive power of existing GNNs is upper-bounded by the 1-Weisfeiler-Lehman (1-WL) graph isomorphism test, which means GNNs that are not able to predict node clustering coefficients and shortest path distances, and cannot differentiate between different d-regular graphs. Here we develop a class of message passing GNNs, named Identity-aware Graph Neural Networks (ID-GNNs), with greater expressive power than the 1-WL test. ID-GNN offers a minimal but powerful solution to limitations of existing GNNs. ID-GNN extends existing GNN architectures by inductively considering nodes' identities during message passing. To embed a given node, ID-GNN first extracts the ego network centered at the node, then conducts rounds of heterogeneous message passing, where different sets of parameters are applied to the center node than to other surrounding nodes in the ego network. We further propose a simplified but faster version of ID-GNN that injects node identity information as augmented node features. Altogether, both versions of ID-GNN represent general extensions of message passing GNNs, where experiments show that transforming existing GNNs to ID-GNNs yields on average 40% accuracy improvement on challenging node, edge, and graph property prediction tasks; 3% accuracy improvement on node and graph classification benchmarks; and 15% ROC AUC improvement on real-world link prediction tasks. Additionally, ID-GNNs demonstrate improved or comparable performance over other task-specific graph networks.
翻译:图像通过神经网络(GNN)为关系数据提供了一个强大的建模框架。然而,现有的GNN的表达力受到1-Weisfeiler-Lehman(1-WL)图形的形态式测试的上限。这意味着无法预测节点组合系数和最短路径距离的GNN无法预测不同的 d-正则图。在这里,我们开发了一个通过GNN(称为身份认知图神经网络)的信息类别,其表达力大于1-WL测试。ID-GNNN为现有GNNN的局限性提供了微弱但有力的解决方案。ID-GNNNNNNN在传递信息时以节点为主,无法区分不同的 d-正方图。在这里,我们开发了一组混杂信息,对中心点应用了不同的参数,而不是对利己网络中的其他节点。我们进一步提议了一个简化但快速的GNNNNNG的精确度链接,在信息传递 GNNNNG 普通版本时,将G 的G 格式转化为 GNNNNNND的G 格式。