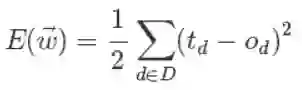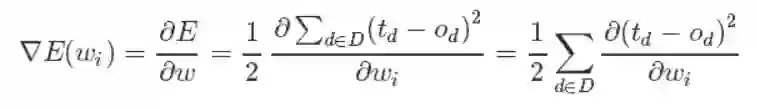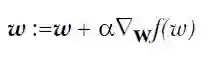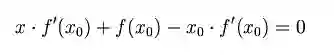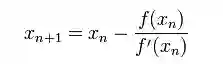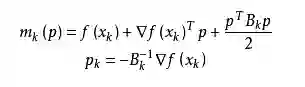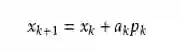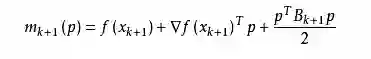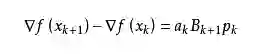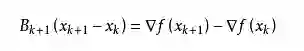BAT机器学习面试1000题系列（第51~55题）

2017 年 10 月 8 日 七月在线实验室 人工智能面试题

（点击上方公众号，快速关注一起学AI）

51.哪些机器学习算法不需要做归一化处理？

概率模型不需要归一化，因为它们不关心变量的值，而是关心变量的分布和变量之间的条件概率，如决策树、rf。而像adaboost、gbdt、xgboost、svm、lr、KNN、KMeans之类的最优化问题就需要归一化。

52. 梯度下降法找到的一定是下降最快的方向么？
梯度下降法并不是下降最快的方向，它只是目标函数在当前的点的切平面（当然高维问题不能叫平面）上下降最快的方向。在practical implementation中，牛顿方向（考虑海森矩阵）才一般被认为是下降最快的方向，可以达到superlinear的收敛速度。梯度下降类的算法的收敛速度一般是linear甚至sublinear的（在某些带复杂约束的问题）。by林小溪（https://www.zhihu.com/question/30672734/answer/139689869）。
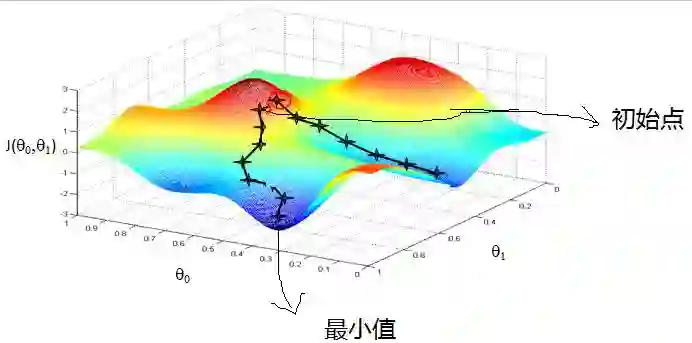
一般解释梯度下降，会用下山来举例。假设你现在在山顶处，必须抵达山脚下（也就是山谷最低处）的湖泊。但让人头疼的是，你的双眼被蒙上了无法辨别前进方向。换句话说，你不再能够一眼看出哪条路径是最快的下山路径，如下图（图片来源：http://blog.csdn.net/wemedia/details.html?id=45460）：

最好的办法就是走一步算一步，先用脚向四周各个方向都迈出一步，试探一下周围的地势，用脚感觉下哪个方向是下降最大的方向。换言之，每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向（当前最陡峭的位置向下）走一步。就这样，每要走一步都根据上一步所在的位置选择当前最陡峭最快下山的方向走下一步，一步步走下去，一直走到我们感觉已经到了山脚。
当然这样走下去，我们走到的可能并不一定是真正的山脚，而只是走到了某一个局部的山峰低处。换句话说，梯度下降不一定能够找到全局的最优解，也有可能只是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

@zbxzc（http://blog.csdn.net/u014568921/article/details/44856915）：更进一步，我们来定义输出误差，即对于任意一组权值向量，那它得到的输出和我们预想的输出之间的误差值。定义误差的方法很多，不同的误差计算方法可以得到不同的权值更新法则，这里我们先用这样的定义：

上面公式中D代表了所有的输入实例，或者说是样本，d代表了一个样本实例，od表示感知器的输出，td代表我们预想的输出。
这样，我们的目标就明确了，就是想找到一组权值让这个误差的值最小，显然我们用误差对权值求导将是一个很好的选择，导数的意义是提供了一个方向，沿着这个方向改变权值，将会让总的误差变大，更形象的叫它为梯度。

既然梯度确定了E最陡峭的上升的方向，那么梯度下降的训练法则是：

梯度上升和梯度下降其实是一个思想，上式中权值更新的+号改为-号也就是梯度上升了。梯度上升用来求函数的最大值，梯度下降求最小值。

这样每次移动的方向确定了，但每次移动的距离却不知道。这个可以由步长（也称学习率）来确定，记为α。这样权值调整可表示为：

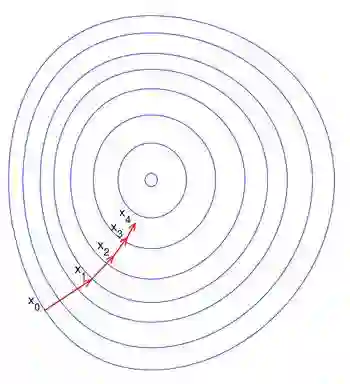
总之，梯度下降法的优化思想是用当前位置负梯度方向作为搜索方向，因为该方向为当前位置的最快下降方向，所以也被称为是“最速下降法”。最速下降法越接近目标值，步长越小，前进越慢。梯度下降法的搜索迭代示意图如下图所示：

正因为梯度度下降法在接近最优解的区域收敛速度明显变慢，所以利用梯度下降法求解需要很多次的迭代。在机器学习中，基于基本的梯度下降法发展了两种梯度下降方法，分别为随机梯度下降法和批量梯度下降法。by@wtq1993，http://blog.csdn.net/wtq1993/article/details/51607040

53. 牛顿法和梯度下降法有什么不同

@wtq1993，http://blog.csdn.net/wtq1993/article/details/51607040
1）牛顿法（Newton's method）

牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x)的泰勒级数的前面几项来寻找方程f (x) = 0的根。牛顿法最大的特点就在于它的收敛速度很快。

具体步骤：

首先，选择一个接近函数 f (x)零点的 x0，计算相应的 f (x0) 和切线斜率f ' (x0)（这里f ' 表示函数 f 的导数）。然后我们计算穿过点(x0, f (x0)) 并且斜率为f '(x0)的直线和 x 轴的交点的x坐标，也就是求如下方程的解：

我们将新求得的点的 x 坐标命名为x1，通常x1会比x0更接近方程f (x) = 0的解。因此我们现在可以利用x1开始下一轮迭代。迭代公式可化简为如下所示：

已经证明，如果f ' 是连续的，并且待求的零点x是孤立的，那么在零点x周围存在一个区域，只要初始值x0位于这个邻近区域内，那么牛顿法必定收敛。并且，如果f ' (x)不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说，这意味着每迭代一次，牛顿法结果的有效数字将增加一倍。

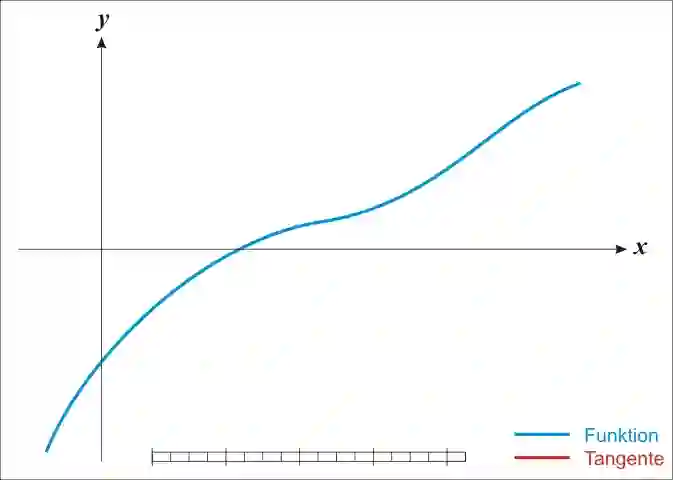
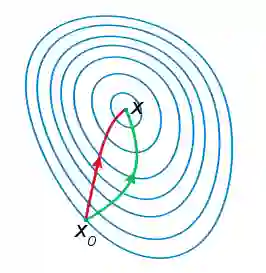
由于牛顿法是基于当前位置的切线来确定下一次的位置，所以牛顿法又被很形象地称为是"切线法"。牛顿法的搜索路径（二维情况）如下图所示：

关于牛顿法和梯度下降法的效率对比：

a）从收敛速度上看，牛顿法是二阶收敛，梯度下降是一阶收敛，前者牛顿法收敛速度更快。但牛顿法仍然是局部算法，只是在局部上看的更细致，梯度法仅考虑方向，牛顿法不但考虑了方向还兼顾了步子的大小，其对步长的估计使用的是二阶逼近。

b）根据wiki上的解释，从几何上说，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。

注：红色的牛顿法的迭代路径，绿色的是梯度下降法的迭代路径。

牛顿法的优缺点总结：

优点：二阶收敛，收敛速度快；

缺点：牛顿法是一种迭代算法，每一步都需要求解目标函数的Hessian矩阵的逆矩阵，计算比较复杂。

54. 什么是拟牛顿法（Quasi-Newton Methods）？

@wtq1993，http://blog.csdn.net/wtq1993/article/details/51607040

拟牛顿法是求解非线性优化问题最有效的方法之一，于20世纪50年代由美国Argonne国家实验室的物理学家W.C.Davidon所提出来。Davidon设计的这种算法在当时看来是非线性优化领域最具创造性的发明之一。不久R. Fletcher和M. J. D. Powell证实了这种新的算法远比其他方法快速和可靠，使得非线性优化这门学科在一夜之间突飞猛进。

拟牛顿法的本质思想是改善牛顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷，它使用正定矩阵来近似Hessian矩阵的逆，从而简化了运算的复杂度。拟牛顿法和最速下降法一样只要求每一步迭代时知道目标函数的梯度。通过测量梯度的变化，构造一个目标函数的模型使之足以产生超线性收敛性。这类方法大大优于最速下降法，尤其对于困难的问题。另外，因为拟牛顿法不需要二阶导数的信息，所以有时比牛顿法更为有效。如今，优化软件中包含了大量的拟牛顿算法用来解决无约束，约束，和大规模的优化问题。

具体步骤：

拟牛顿法的基本思想如下。首先构造目标函数在当前迭代xk的二次模型：