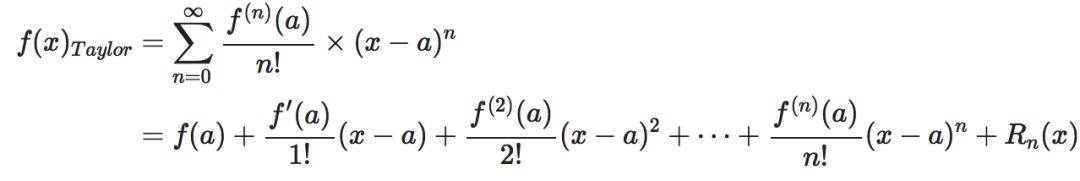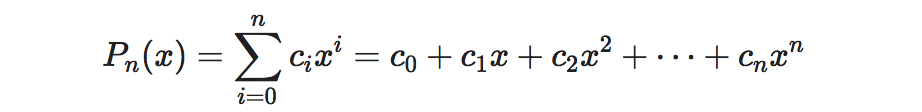【机器学习数学基础】动图解释泰勒级数（一）

在遇到一个生僻的概念或者公式时，确认它的几种不同的表述形式（马甲）是很重要，也就是定义问题：我们到底要了解的东西是什么 ＆ 怎么称呼：

泰勒公式（也叫 泰勒展开式、泰勒多项式）
泰勒级数

它是微积分学下的一个重要概念，与之有关联的有：如泰勒定理，多元泰勒公式，以拉格朗日型余项为代表的各类余项，审敛法，牛顿差值公式（牛顿级数）（列出为了进行树状知识整合和梳理）

1

什么是泰勒公式

基本定义：

数学定义，公式各个部分代表什么含义先说清楚

个人粗浅总结，初学者产生记不住的感觉大多数情况下是没有沉下心来想想公式的各部分表示的是什么东西，梳理一下会清晰很多

联想链条

首先拆字

【公式】 ＜什么公式？＞➜ 【多项式】（Polynomials），把多项式的一般形式写出来，这应该是非常容易理解的概念，即指数不仅仅为2的抛物线的组合

【泰勒】＜谐音“太乐” ≈ 如果所有小数都能近似成整数那不是太快乐了？＞ ➜ 近似，获得一个直观理解

• 泰勒公式通过把【任意函数表达式】转换（重写）为【多项式】形式，是一种极其强大的函数近似工具

为什么说它强大呢？

• 多项式非常【友好】，三易，易计算，易求导，易积分

• 几何感觉和计算感觉都很直观，如抛物线和几次方就是底数自己乘自己乘几次

泰勒公式干的事情就是：使用多项式表达式估计（近似）f(x)在x=a附近的值

那么如何近似呢？使用一个例子来加深理解

转自：机器学习算法与自然语言处理

完整内容请点击“阅读原文”