【ICLR2020】Transformer Complex-order：一种新的位置编码方式

会员服务 ·

【ICLR2020】Transformer Complex-order：一种新的位置编码方式

2020 年 2 月 24 日 AINLP

补一下昨天没发完的一篇文中公式若显示不全可左右滑动~

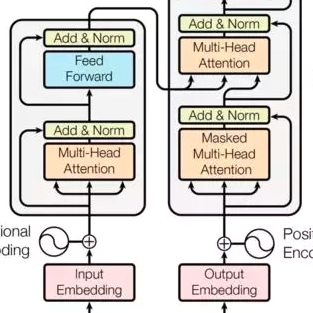
比较有意思的论文^[1]，关注的点也是在序列建模的位置信息编码。先前的方法通过引入额外的位置编码，在 embedding 层将词向量和位置向量通过加性编码融合，

但是该种方式每个位置向量是独立训练得到的，并不能建模序列的order relationship（例如邻接或优先关系），作者将此称为the position independece problem。

针对该问题论文提出了一种新的位置编码方式，将独立的词向量替换成自变量为位置的函数，于是单词表示会随着位置的变化而平滑地移动，可以更好地建模单词的绝对位置和顺序信息。

其中，表示此表中序号为的单词在位置时的单词向量，表示函数集合，表示单词到函数的映射，展开即为，

为了达到上述要求，函数应该满足以下两个条件：

Property 1. Position-free offset transformation

对于任意位置 pos 和，存在变换 Transform Transform 满足，

特别地，论文考虑 Transform 为线性变换

Property 2. Boundedness

函数应该是有界的，

接下去，论文证明了满足上述两个条件的解函数形式为，

❝
贴一下论文给的证明：（看不看无所谓，能用就行 haha）
假设函数满足上述两个条件，则对于任意位置，有

因此有。我们令以及，由于是任意的，有

当pos 时，有

当pos =1时，有

综上将上述所有情况综合有

发现当，就不是有界的了，因此限制后，有

这样就满足有界性的条件了；
又由和 Transform pos 得，对所有的位置 pos，

得证。

根据欧拉公式，可以将上述解函数转化为，

在实现过程中，由于上述的限制会导致优化问题，因此一种自然而然的做法就是固定，于是上式可以简化为，

最终的 embedding 表示为，

其中振幅、角频率和初相是需要学习的参数。

振幅只和单词本身有关，即原本的词向量；
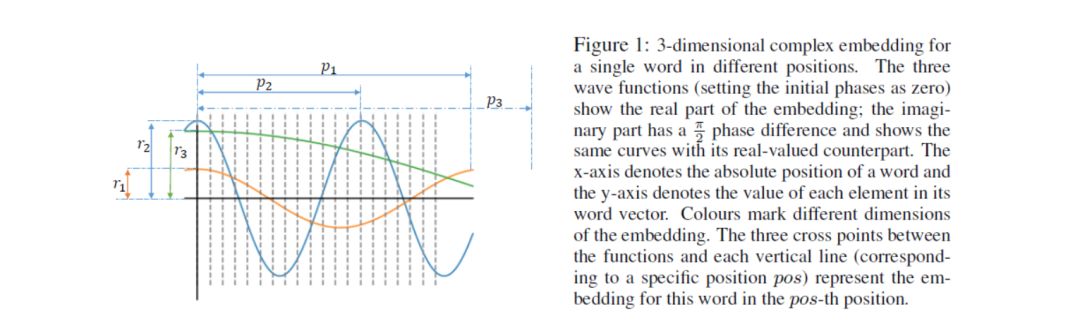
角频率决定单词对位置的敏感程度。当角频率非常小时（如下图 p1），单词对于所有位置的词向量基本保持不变，这就与标准词向量一样了；

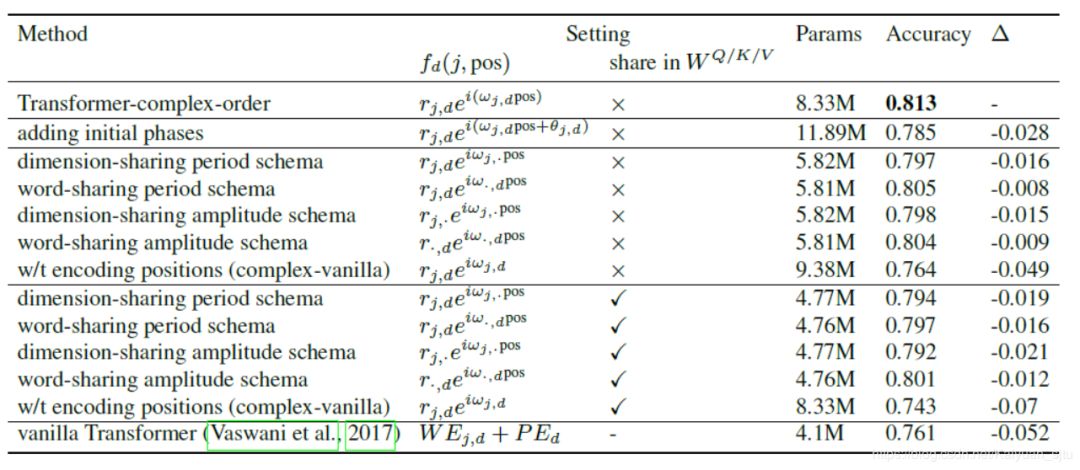
简单看一下文本分类任务的消融性分析结果：

增加可学习初相之后效果比设置初相为 0 差：

"The negative effect of initial phases may be due to periodicity, and cannot be directly regularized with L2-norm penalties."

设置参数共享策略之后（word-sharing scheme和dimension-sharing scheme）效果变差，可能是由于参数变少导致学习表征能力下降；

一些思考：

❝1. 要用的话，计算量以及参数量是不是会很大呀；

❝2. 好像也没看到跟其他 relative position 的模型比较

reference

Code Here ^[2]
Open Review ^[3]

本文参考资料

[1]

Encoding Word Order in Complex Embedding: https://openreview.net/pdf?id=Hke-WTVtwr

[2]

Code Here: https://github.com/zhaodongh/Encoding-Word-Order-in-Complex-valued-Embedding

[3]

Open Review: https://openreview.net/forum?id=Hke-WTVtwr

- END -

推荐阅读

AINLP年度阅读收藏清单

Transformers Assemble（PART III）

Transformers Assemble（PART II）

Transformers Assemble（PART I）

站在BERT肩膀上的NLP新秀们（PART I）

站在BERT肩膀上的NLP新秀们（PART II）

站在BERT肩膀上的NLP新秀们（PART III）

大幅减少GPU显存占用：可逆残差网络(The Reversible Residual Network)

鼠年春节，用 GPT-2 自动写对联和对对联

transformer-XL与XLNet笔记

AINLP-DBC GPU 云服务器租用平台建立，价格足够便宜

征稿启示 | 稿费+GPU算力+星球嘉宾一个都不少

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLP君微信(id：AINLP2)，备注工作/研究方向+加群目的。