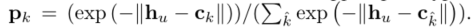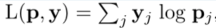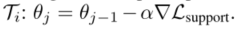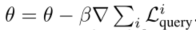NeuralPS'20 | Graph Meta Learning via Local Subgraphs

1. 论文背景

G-META 是第一个使用局部子图来进行元学习的模型。目前流行的图学习方法需要丰富的标签和边缘信息。当新任务的数据缺乏时，可以使用meta-learning(元学习)从以前的经验中学习以快速适应新任务。本文提出了一种新的图元学习算法G-META。它通过局部子图来传递子图特有的信息，并通过meta gradients(元梯度)更快地学习可转移的信息。

论文题目

Graph Meta Learning via Local Subgraphs

论文时间

NeuralPS 2020

2. 论文方法

2.1 问题定义

设   为n个图，其中   ，V、E分别为点和边的集合，X为点v的属性向量；   为不同的label；S为子图。

图神经网络背景：

（1）Neural message passing：指每个连接的uv结点的信息，   。

（2）Neighborhood aggregation：指将结点u与其邻域   中的结点的信息聚合，   。

（3）Update：最后GNN通过非线性函数更新node embedding，   。

元学习背景：

meta-set由   组成。每个meta-set有许多tasks，每个task可以被分为   ，support用于学习而query用于评估。Model-Agnostic Meta-Learning (MAML) 的目标是可以快速获得一个参数初始值来适应未见的任务。

G-META的核心原则是用局部子图表示节点，然后使用子图在任务、图和标签集之间传递信息。

结点分类的目标是通过少量数据可以精确将结点v的子图映射到它的标签上。

2.2 G-META

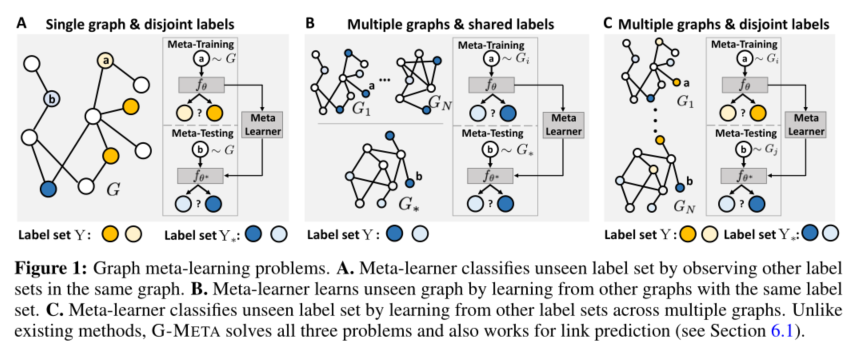
如图1所示，本文将meta-learning分为三类：

A. 通过观察同一图中的其他标签集来对看不见的标签集进行分类。B. 通过学习具有相同标签集的其他图来学习看不见的图。C. 通过学习多个图上的其他标签集来对看不见的标签集进行分类。

2.2.1 定理

本文证明了两个定理：

（1）Decaying Property of Node Influence ，即随着节点距离的增加，节点之间的影响呈指数型下降。

（2）Local Subgraph Preservation Property ，即基于局部子图的分析是基于全局图分析的近似。

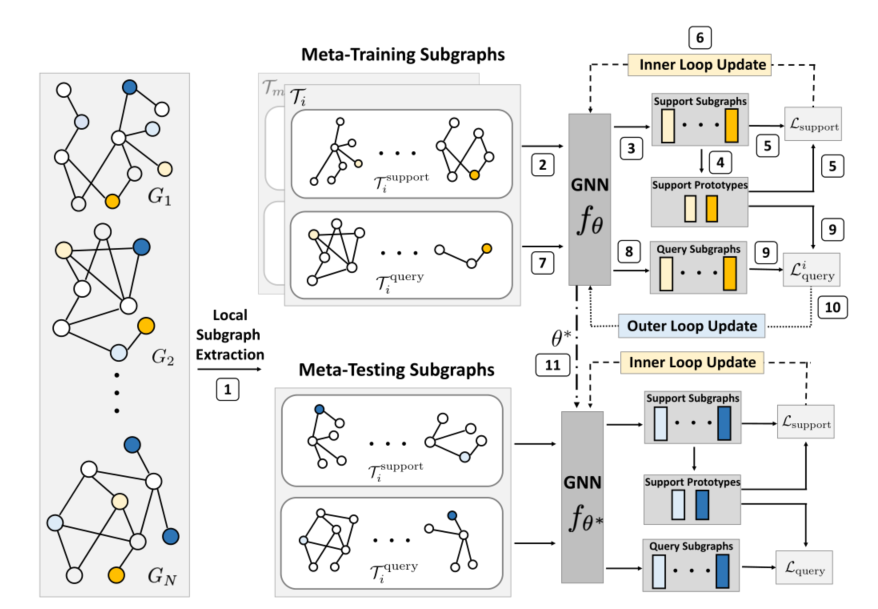
2.2.2 框架

子图编码

在每个任务中首先通过结点u的k-hops邻居构造u对应的子图   ，之后将子图放入GNN获得对应的embedding。

u作为子图的centroid node(质心结点)，它的embedding被用来表示子图    。

原型损失

在获得子图表征之后，我们利用表征和标签之间的归纳偏差来规避标签有限的问题。

对于每个标签k，取支持集子图embedding的均值来获得prototype(原型)    并作为标签k的标志。

之后类分布向量P由支持集原型和质心embedding的欧式距离计算出来：

最后，我们使用局部子图的类分布向量来优化交叉熵损失:

Optimization-based meta-learning

本文使用MAML在图和标签之间传递结构信息。

在元训练inner loop中，我们对每个任务的支持损失进行规则的随机梯度下降：

然后使用查询集评估更新后的参数，然后我们执行元更新步骤:

重复执行上述步骤，最后的\theta^*是快速适应看不见的任务的最佳参数。

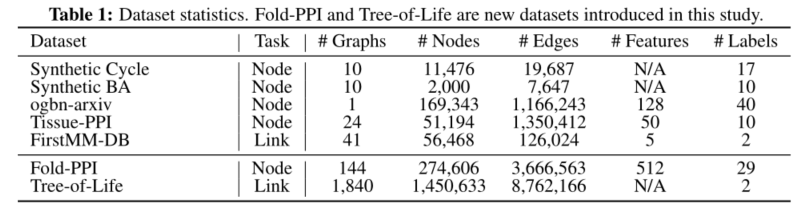
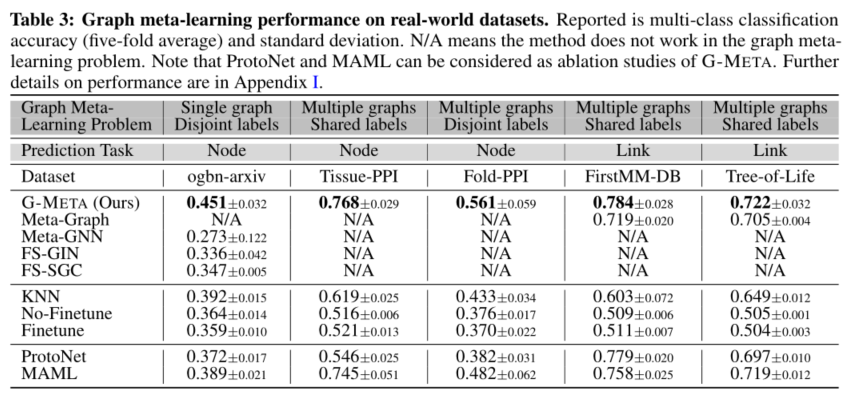
3. 实验

本文使用三个真实世界的数据集进行节点分类和两个链接预测来评估G-META。