Arxiv'21 | Graph Federated Learning

前言

在一般联邦学习框架中，训练过程包括中央服务器和本地客户端多个 epoch 的数据通信，在处理敏感数据时可能存在隐私泄露问题，因此，有必要对算法进行私有化。此外该架构对服务器上的通信故障和计算过载非常敏感。

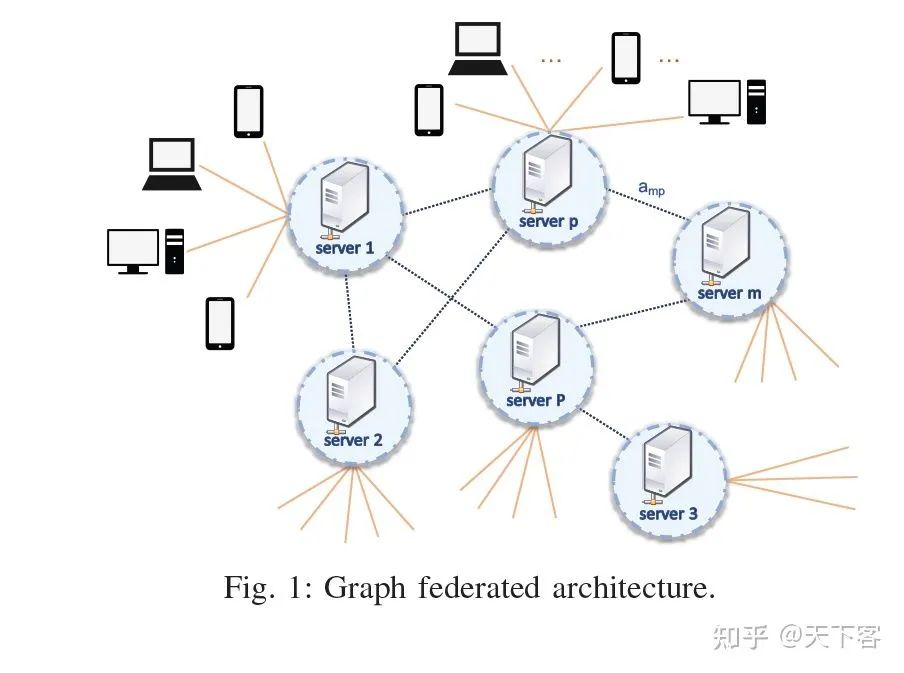
本文提出 graph federated learning（GFL）来解决传统 FL 中一个服务器来进行所有通信和聚合所导致的鲁棒性问题。GFL 由几个服务器组成，每个服务器都与自己的客户端子集相连。服务器之间的连接由图结构来表示。具体来说使用密码学和差分隐私的概念，将联邦学习算法私有化，并将其扩展到图结构中。本文研究了私有化对算法性能的影响，私有化可以被建模为加性噪声并表明在凸性和 Lipschitz 条件下，私有化过程与非私有化算法的性能相近。

1. Problem setup

在 GFL 算法框架下包含 个服务器，每个服务器与 个本地客户端集合相连，服务器之间的 通信拓扑可以表示为一个组合矩阵 ，其中每一个元素表示为 ，算法的目标函 数为最小化平均经验风险:

其中每一项的经验风险 可以以损失函数的形式进行表示 :

其中 对应于服务器， 对应于客户端， 对应于数据。每个服务器与它客户端集合使用 FedAvg 机制进行本地训练和训练结果的聚合，然后服务器之间运行一个共识类型算法。当每个本 地客户端在向服务器发送最终更新之前经过不同的 epoch，所产生的增量误差在 的数量 级上，并且由梯度噪声所主导。因此简化问题，假设集合 中的 个采样客户在每次迭代中 运行一次 SGD。形式化表示为，在第 次迭代，每个客户端 更新在服务器的权重参数 为 。进而将更新后的结果发送给给服务器

其中 表示由客户端 在第 个 epoch 中所采样的 mini-batch，其所属于服务器 并 且采样大小为 。基于此相邻的服务器之间相互交流收到的更新信息:

最后得到更新后的模型权重:

为了给算法引入隐私保护，在每轮通信期间发送的更新可以被一些噪音所干扰。在第 次迭代， 设 为服务器 所添加的发送给服务器端 的噪音, 为由客户端 所添加的发 送给服务器端 的在第 次迭代的噪音。上述过程可总结为:

1. 客户端更新本地模型权重过程，式 (6)
2. 服务器聚合客户端权重发送结果过程，式 (7)
3. 服务器间通信组合权重过程，式 (8)

此外，如果使用 SMC（秘密共享），可以通过一个可逆函数 对协议进行建模，将本地更新 映射到加密的版本。在服务器聚合式 (7) 和服务器组合式 (8) 步骤中，分别用 和 代替 和 。

2. Analysis（略）

凸优化及隐私分析（详情可见 III. PERFORMANCE ANALYSIS、IV. PRIVACY ANALYSIS）

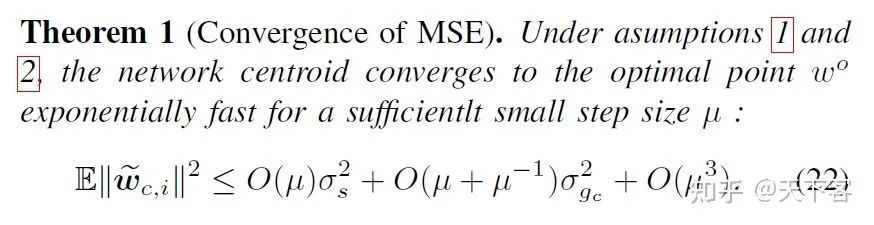
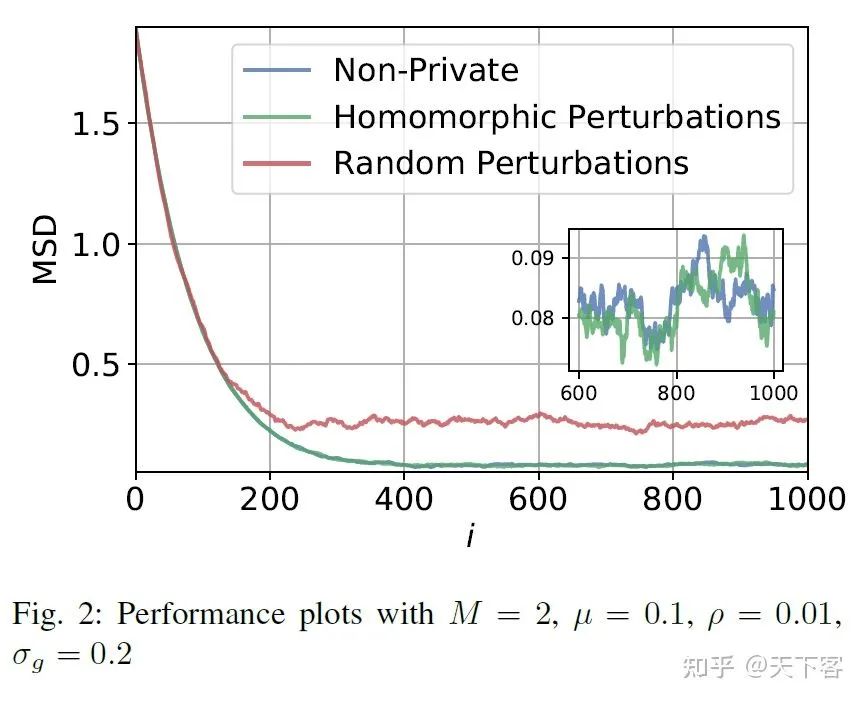
3. Experiments

将本文所提出的私有方法与使用标准扰动的标准私有算法，以及非私有算法进行比较：