贝叶斯神经网络(系列)第一篇

本文为 AI 研习社编译的技术博客，原标题 ：

Bayesian Neural Network Series Post 1: Need for Bayesian Neural Networks

作者 | Kumar ShridharFollow

翻译 | mashagua            

校对 | 酱番梨        审核 | 约翰逊·李加薪       整理 | 立鱼王

原文链接：

https://medium.com/neuralspace/bayesian-neural-network-series-post-1-need-for-bayesian-networks-e209e66b70b2

注：本文的相关链接请访问文末二维码

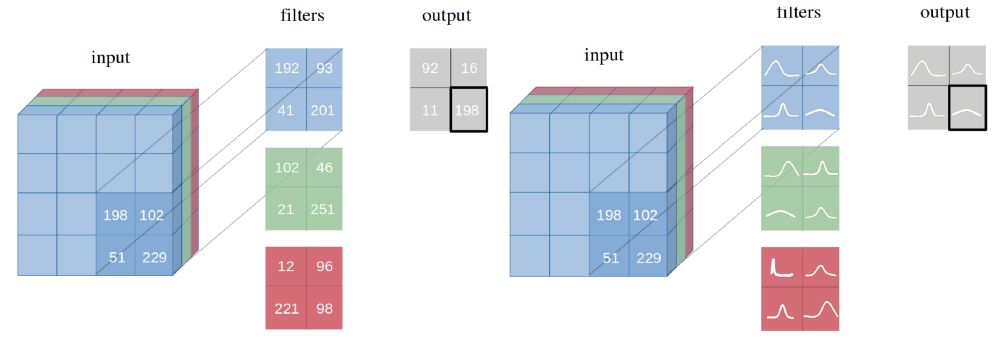
图1：点估计作为权重的神经网络 vs 概率分布作为权重的神经网络。

这篇文章是贝叶斯卷积网络八个系列中的第一篇文章。  这些博客的大致结构如下：

1. 贝叶斯网络的应用场景

2. 为了更好的理解贝叶斯网络所需要的背景知识

3. 一些在贝叶斯神经网络方面最新的成果

4. 基于变分推理的贝叶斯卷积神经网络

5. 利用PyTorch 建立你自己的贝叶斯卷积神经网络

6. 贝叶斯神经网络的不确定性估计

7. 贝叶斯神经网络中的模型修剪

8. 在其他领域的应用（超级分辨率，GAN等...）

让我们通过本篇博客理解贝叶斯神经网络的需求场景来开始这个系列。

  问题陈述

深度神经网络（DNNs）是通过学习示例来学习执行任务，而无需事先了解任务的连接系统。它们可以轻松扩展到数百万个数据点，并且可以通过随机梯度下降进行优化。

卷积神经网络（CNN）是DNNs的一个变体，已经在图像分类领域超越了人类的准确性。由于CNNs可以拟合各种非线性数据点，因此它们需要大量的训练数据。这会导致CNN和一般的神经网络经常在每类具有少量的训练样例上造成过拟合。神经网络模型可以在训练集上拟合的很好，但是不能很好的预测未曾出现的数据。这种情况经常会造成神经网络无法正确评估训练数据中的不确定性，从而导致对正确的类别，预测或行动的过度自信的决定。

如果博客的这部分对你来说有点超前，那么建议你从这里重新回顾一下深度学习的基本知识。

为了理解这部分，让我们考虑一个猫狗图像的二分类训练任务。现在，当一个豹子的图片出现在测试集中，理想情况下模型应该预测它既不是狗也不是猫（狗的概率为50％，猫类概率为50％）。但是，由于输出层的softmax函数可以获得概率分数，它会调整一个类输出概率分数并最大化另一个类，从而导致一个类的置信度过高。这是点估计神经网络的主要问题之一。

注意到点估计应用在神经网络，其中权重由单个节点表示。另一方面，一个贝叶斯神经网络的权重是由它的分布表示，可见图一。

但是我们真的需要贝叶斯神经网络吗？在工程实践中我们用各种正则化技巧去控制过拟合，比如，提前终止迭代，权重衰减，L1或者L2正则化以及最近流行的并且经验上非常有效的技术，丢弃一些神经网络的节点。

如果我们通过对模型进行正则化可以解决决策置信度过高并且防止模型过拟合，那么问题仍然存在：为什么我们需要贝叶斯神经网络？  

简言之，答案是：当前神经网络架构中缺少预测中的不确定性度量，但贝叶斯神经网络将其纳入其中。

  发展现状

深度神经网络已经成功的应用在很多领域，包括一些非常敏感的领域，像医疗，安防，欺诈性交易等等。这些领域严重依赖模型预测的准确度，并且甚至一个过度自信的决策可以导致大问题。并且，这些领域的数据集非常不平衡（百万分之一的欺诈交易，接近5%的癌症阳性，不足百分之一的垃圾邮件），这种情况会导致模型在采样的类别上发生过拟合现象。

从概率论的角度来说，使用点估计作为基于任何分类的权重是不合理的。另一方面，贝叶斯神经网络在过拟合现象上更加鲁棒，并且能很好的从小的数据集当中学习。贝叶斯方法通过其参数以概率分布的形式进一步提供不确定性估计（见图1）。同时，通过使用先验概率分布来整合参数，在训练期间在许多模型上计算平均值，这给网络提供正则化效果，从而防止过度拟合。

  贝叶斯神经网络的实用性

贝叶斯神经网络通过参数进行后验推断从而防止过拟合在理论上来说是一个有吸引力的方法  ，然而，之前从未成功地对CNN的内核（也称为滤波器）进行分布建模，可能是因为在实际应用中常用的大量参数和极大模型。

即使是一个数量非常少的参数集，利用贝叶斯神经网络进行推断后验估计也是一个非常困难的任务。通常使用模型后验的近似值，变分推理是一种流行的方法。在这里，人们将使用简单的变分分布（例如高斯分布）对后验进行建模，并尝试使分布的参数尽可能接近真实的后验。这个通过最小化简单的变分分布和真实后验分布的Kullback-Leibler差异来完成。许多人过去都采用过这种方法来处理标准神经网络模型。

但是用变分方法来估计贝叶斯网络中的后验估计计算量非常大。使用高斯近似分布会大大增加模型参数的数量，而不会大幅增加模型容量。例如， Blundell et al. (2015),使用贝叶斯神经网络后验近似的高斯分布，并且模型参数的数量加倍，但报告与使用丢弃部分节点的传统方法有着相同的预测性能。这使得该方法在实践中不适合与CNN一起使用，因为参数数量的增加代价太大

  接下来我们该怎么做？

有很多种方法构建贝叶斯神经网络（在第三篇博客中我们会考虑到很多种）。然而，在这个系列中，我们将专注于使用Backprop的Bayes方法构建贝叶斯CNN。关于神经网络权重的贝叶斯精确推断是难以处理的，因为参数的数量非常大，并且神经网络的功能形式不适合精确积分。因此我们将会把难以处理的真实后验估计概率分布p(w|D)用带有变分的概率分布q_θ(w|D)去做近似，它符合高斯分布μ∈ℝ^ d和σ∈ℝ^ d的性质，表示为N（θ |μ，σ²），其中d是定义概率分布的参数总数。。这些高斯变分后验分布的形状由它们的方差 σ²决定，表达了一种对于每个模型参数估计的不确定性。

 由Graves（2011）提出的上述的图形直觉。

如果你不能准确的理解我们之前的篇章段落，没关系。在下一篇博客中我们将会介绍理解贝叶斯神经网络所用到的所有基础知识。

  接下来的几周我们期望做的事情：

1. 我们将看到Backprop方法如何将Bayes有效地应用于CNN。我们将介绍应用两个卷积运算的想法，一个用于均值，一个用于方差。

2. 我们将会看到模型如何从多个简单的模型平均中学习到更为丰富的表现形式和预测结果。

3. 我们将看到，贝叶斯CNN的所提出的通用且可靠的变分推理方法可以应用于各种CNN架构，而不受其性能的任何限制。我们将在PyTorch中对模型进行编码，并将结果与点估计网络进行比较。

4. 我们将估计贝叶斯神经网络中的任意和认知不确定性。更进一步，我们将凭经验证明不确定性如何降低，使得网络做出的决策随着训练准确性的提高而变得置信度更高。

5. 我们将会学习到我们的方法通常使模型的参数增加两倍，并且我们可以通过一个关于梯度的无偏的蒙特卡洛模拟方法训练一个无穷集合。

6. 我们将L1范数应用于训练的模型参数并修剪非零值的数量。另外我们会用一个预训练好的模型去微调模型从而达到减少模型参数而不改变模型准确度的目的。

7. 最后，我们将会应用贝叶斯CNN应用到图像超分辨率和生成对抗网络等任务，我们将结果与相应领域中的其他重要架构进行比较。

想要继续查看该篇文章相关链接和参考文献？

点击底部【阅读原文】或长按下方地址/二维码访问：

https://ai.yanxishe.com/page/TextTranslation/1465