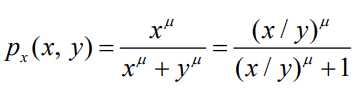战斗行动建模是一项紧迫的科学和实践任务,旨在为指挥官和总部提供决策的量化依据。
作者根据G-塔洛克的冲突函数(function of conflict),并考虑到战斗(军事)行动的规模,提出了战斗和军事行动中的胜利函数(function of victory)。通过足够数量的军事统计数据,对尺度参数进行了评估,并为战术、战役和战略层面找到了其数值。研究了"进攻-防御"(«offensive – defense»)的博弈论模型,“进攻方”与“防御方”由一个或几个部队梯队组成,在博弈论模型中各方解决当前和随后的任务。在建模的第一阶段,找到了当前任务的解决方案--突破(守住)防御点,在第二阶段,找到了后续任务的解决方案--在防御纵深击败敌人(反攻和恢复防御)。在战术层面上,利用纳什均衡,根据三个标准为对抗性博弈中最接近的问题(双方力量在防御点的分布)找到了解决方案:a)突破最弱的点,b)至少突破一个点,c)加权平均概率。研究表明,在其他条件相同的情况下,进攻方最好使用 "至少突破一个点 "的标准,可以确保突破防御点的最大概率。在对特定情况进行建模的第二阶段(双方在突破和守住防御点时以突破最弱点的标准为指导),根据两个标准解决在战术任务(梯队)之间分配部队和设施的问题:a)突破防御点的概率和在纵深防御中击败敌人的概率最大化,b)概率的最小值最大化(保证结果的标准)。感知是作战行动的一个重要方面。考虑了反射性博弈(以复杂的相互认识为特征的博弈)和信息管理的几个例子。它显示了在什么条件下信息控制会增加参与者的回报,并找到了最佳信息控制。
【关键词】数学模型、战斗、进攻、防御、胜利函数、博弈论模型、反射性和信息控制
1 引言
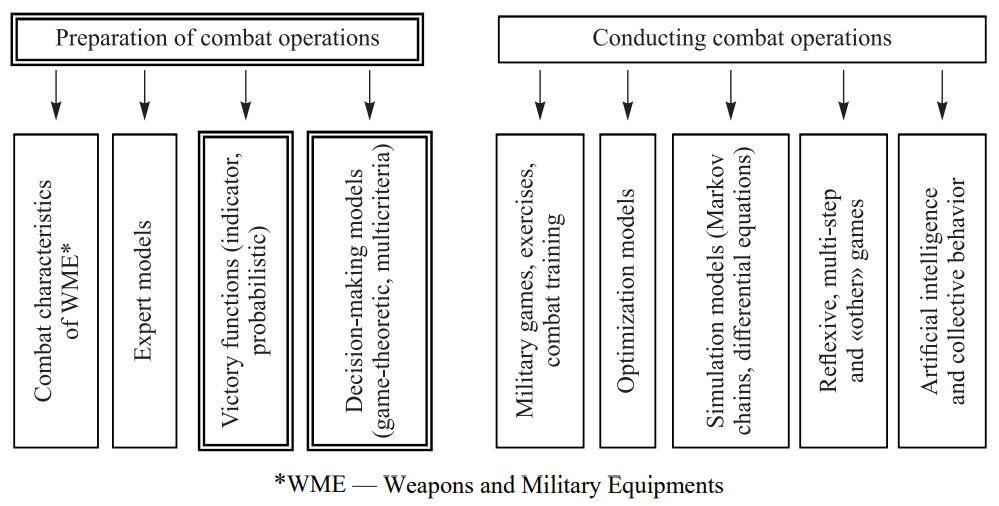
对部队的控制是指挥官、总部和其他指挥和控制机构为保持部队的战备和战斗力、为战斗做准备并指导他们执行指定任务而进行的有目的的活动[Taktika, 1987]。部队指挥与控制的两个主要阶段(战备和执行战斗行动)可以用一套模型表示,其分类见图1。
图1:战斗行动分类模型
-
战斗行动准备阶段
- WME的战斗特征
- 专家模型
- 胜利函数(指标,概率)
- 决策模型(博弈论,多准则)
-
战斗行动执行阶段
- 军事游戏,演习,战斗训练
- 优化模型
- 仿真模型(马尔科夫链,微分方程)
- 反射性的、多步的和其他的博弈
- 人工智能与集群行为
在准备阶段,在一般情况下,战斗行动的建模归结为找到部队的部署最佳方案(将部队和设施部署到该地区,并分配),可对敌人造成最大可能的损害。建模的顺序如下:
在第一阶段,分析战斗资产的战术特征,并计算出在战斗、战役、行动中预期的编队参数(单位、小型/大型单位)(可能有专家参与),能在道德和技术上对敌方编队形成战斗优势[Buravlev, Tsyrendorzhiev, Brezgin, 2009; Dorokhov and Ishchuk, 2017] 。
在第二阶段,选择形成胜利函数的类型[Shumov, 2020]:指标型(Blotto上校博弈[Application, 1961])或概率型,在概率型情况下,基于比率(Yu. B. Germeier[Germeier, 1971],G. Tullock[Tullock, 1980]的函数),或基于力差(D. McFadden和D. Hirschleifen的模型[Jia, Skaperdas, Vaidya, 2013])。
在第三阶段,建模通常包括设定博弈论任务 "进攻-防御",并为任务和点(区域、阵地)之间的部队分配找到最佳方案。如果可能的话,在突破防线和深入防线的过程中,也要对进攻进行规划(预测),并对误导敌人的活动进行检验。
在最后阶段,对模型进行验证,检查计算结果是否符合军事艺术原则和作战经验(模型 "正确性"的标准是模拟结果是否符合军事艺术原则[Osipov, 1915])。
战斗行动执行(控制的第二阶段)是在战斗行动过程中使用模拟和其他模型以及具有不同自动化程度的决策支持系统进行的军事游戏、演习和战斗训练中探讨的[Novikov, 2012; Aggregated, 2000],不是本文的主题。
俄罗斯将军米哈伊尔-帕夫洛维奇-奥西波夫(Mikhail Pavlovich Osipov)被认为是战斗行动模拟的创始人。他在1915年发表在《军事文集》(现在的《军事思想》杂志)上的作品《战斗人员数量对其失败的影响》[Osipov, 1915]中,根据对19世纪和20世纪38次常备部队战斗结果的分析,阐述了一个战斗动力学模型,找到了解决方案,并估算了模型参数。
Osipov-Lanchester模型[Osipov, 1915; Lanchester, 1916](平均动力学方法)的正式论证可以在[Wentzel, 1964]中找到。对抗性博弈理论的基本概念是由E.Borel[Borel, 1921]提出的。在俄罗斯和国外,作战行动模型是在 "运筹学 "的科学学科框架内发展起来的(例如,见作品[Germeier, 1971; Krasnoshchekov, Petrov, 1983; Vasin, Morozov, 2003; Vasin, 2005; Vasin, Krasnoshchekov, Morozov, 2008; Morse and Kimball, 1951; Karlin, 1964; Wagner, 1972] )。经典的博弈论问题 "进攻-防御 "是由Yu. B. Germeier[Germeier, 1971]提出和解决的(作为O. Gross模型的修改),双方在防御点之间分配有限资源。
D.A. Novikov的文章 "Hierarchical models of warfare(战争的分层模型)"[Novikov, 2012]中可以找到关于作战行动建模的概述,其中考虑了兰彻斯特模型、Blotto上校博弈(一种双方同时独立地在对象--战场、同时竞争/拍卖、选民群体等之间分配资源的博弈),以及指标和概率类型的冲突函数。
主体根据关于基本参数的层次观念做出决定,不可避免地,由于这样或那样的原因,观念(反身现实)和客观现实之间存在差异。控制科学中对反射性系统研究始于20世纪60年代[Lefevre, 1973],在过去的十年中,一套信息和战略反射性数学模型已经被开发出来[Novikov, Chkhartishvili, 2012]。
本文的目的是在以下方向概括和阐述作战行动模拟的结果[Korepanov, Novikov, 2011;Shumov, 2019;Shumov, Korepanov, 2020;Shumov, Korepanov,2021]:
-
首先,考虑到作战单位的道德和技术特点、作战行动的规模,对战斗、战役、行动中的胜利函数进行统计论证。
-
第二,开发博弈论的 "进攻-防御 "模型,其中进攻方解决两个任务:第一阶段任务(突破敌人的防御)和随后的任务(摧毁敌人的储备,在防御的深处夺取目标物)。请注意,在现有的博弈论模型中,只有第一个任务被形式化,也就是说,这种模型可以被称为反击模型,而不是进攻(防御)模型。
-
第三,考虑战斗模型中双方的态势感知。
因此,下面考虑的战斗模型的一个特点是在其中使用胜利函数,表示冲突的对立性质:第一方努力的增加以及第二方努力的减少,会提升第一方成功的机会[Hirshleifer, 2000]。这项工作的主要重点是分析胜利函数和解决任务和方向(物体、点)上资源最佳分配的博弈论问题。
2 “进攻-防御”博弈论模型
“进攻-防御”博弈论模型是在格罗斯-格梅尔-瓦辛(Gross – Germeier – Vasin)"进攻-防御"模型的基础上开发的[Karlin, 1964; Germeier, 1971; Vasin, Morozov, 2003],主要在突破防御点任务方面做了研究。战斗(战役、行动)中的胜利函数被用作战斗技术的聚合函数。
假设双方都参与了冲突(竞争、拍卖)。他们的努力(资源)将分别用x>0和y>0来表示。双方努力的任何组合都被赋予成功(胜利)的概率--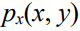
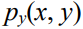
其中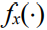
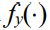
其中