25节课学完线性代数，UCLA教授Artem Chernikov的教学课程视频上线了

转载机器之心

编辑：蛋酱

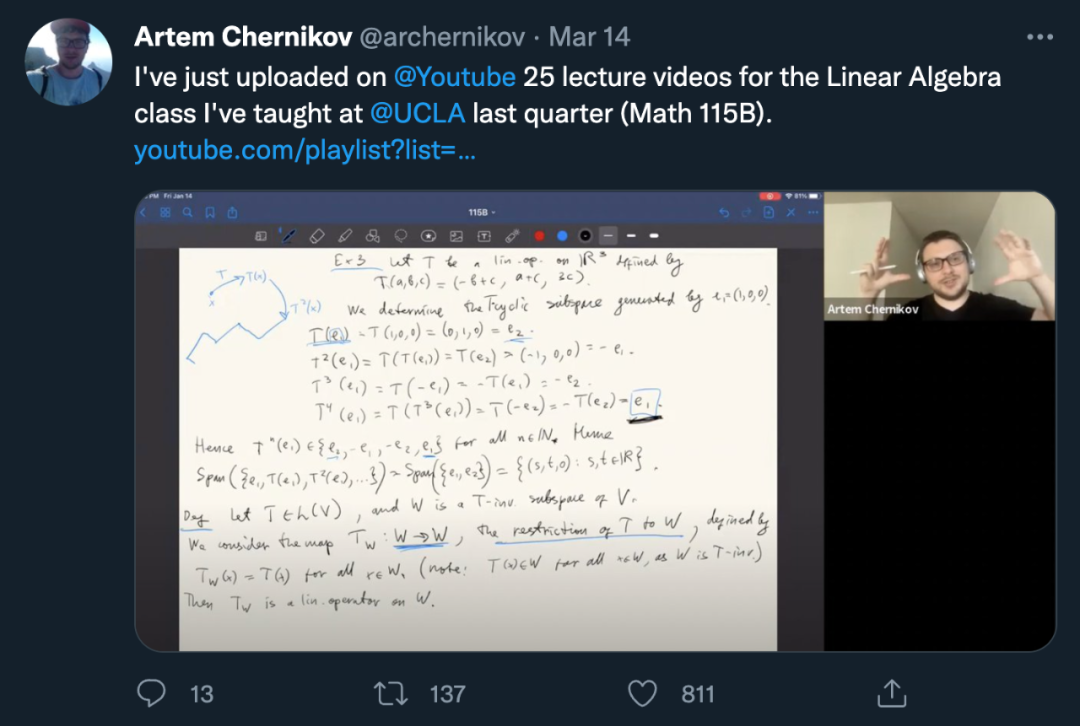
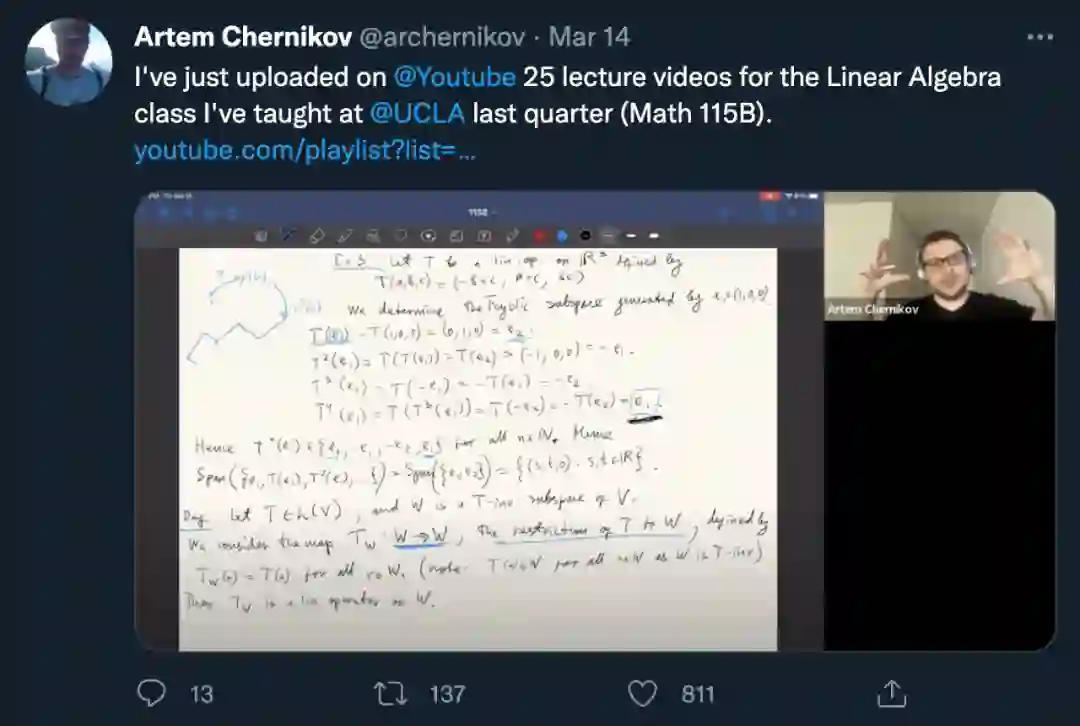
视频提供了详细的课堂笔记，但是没有字幕。 近日，UCLA 教授 Artem Chernikov 宣布自己的线性代数课程 UCLA MATH 115B 全部内容已在 YouTube 平台公开。

Artem Chernikov 现为 UCLA 副教授，同时也是 UCLA Logic Center 的成员。他的主要研究兴趣是数理逻辑的一个分支「模型理论」，更具体地说，包括 Shelah 分类 (稳定性、简单性、NIP、NTP2...) 及其在代数、几何、组合学和计算机科学上的应用。

根据个人简历介绍，Artem Chernikov 本科阶段就读于俄罗斯圣彼得堡国立电信大学，2012 年在里昂第一大学获得博士学位，2015 年加入 UCLA，并在 2022 年获得教授职位。 线性代数和微积分一样，是高等数学的两大入门课程之一。除此之外，它也是一门非常好的工具学科，在很多领域都有广泛的用途。

Artem Chernikov 的《线性代数》课程共分为 25 节，每节课的时长都在 60 分钟以下，且展示了完整的讲义。课程目录如下：

1. 向量空间
2. 基础，维度和线性变换
3. 双重空间
4. 线性算子的转置与二重对偶空间
5. 特征值、特征向量和特征空间
6. 不变子空间和循环子空间
7. 不变子空间和 Cayley-Hamilton 定理
8. Cayley-Hamilton 的证明，子空间直和9、子空间直和与对角化
9. 直和与特征多项式，内积空间
10. 内积空间，伴随算子
11. 特征向量和标准正交基，舒尔引理
12. 正规算子
13. 自伴算子，等距
14. 酉算子和正交算子
15. 矩阵的酉正交等价，正交投影
16. 正交投影（续）
17. 谱定理
18. 正交算子几何：旋转和反射
19. 正交算子的几何分类
20. 正交算子的分类，若当标准型
21. 若当标准型：广义特征向量和特征空间
22. 广义特征空间及其基的分解
23. 广义特征向量的循环
24. 若当标准型的存在性

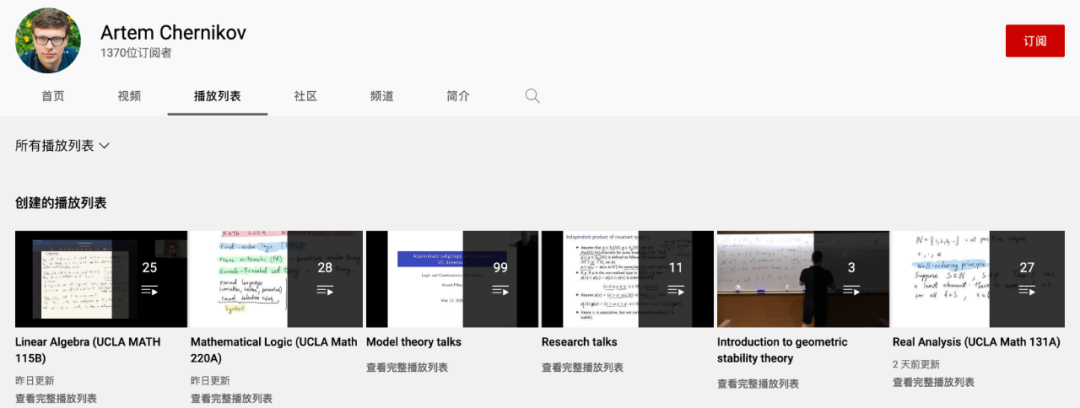
目前，Artem Chernikov 也在自己的 Youtube 频道上传了其他课程的视频。

频道主页：https://www.youtube.com/c/archernikov

此前，机器之心也曾介绍过 88 岁高龄 MIT 教授 Gilbert Strang 的线性代数课程，感兴趣的读者也可进行参考。

推荐阅读：85岁MIT教授Gilbert Strang《线性代数》2020视频课，不怕学不会的线代