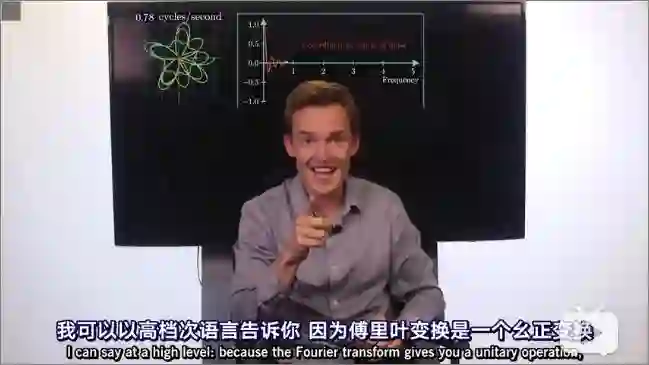
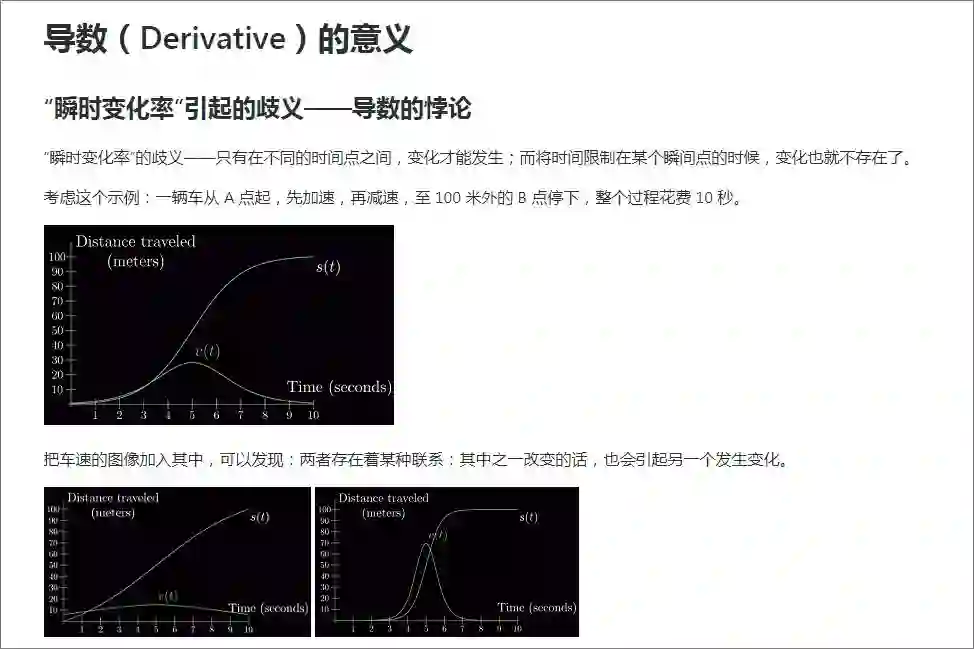
机器学习入门 | 刷新你三观的高数和线代教程

来自：高级农民工（微信号：Mocun6）

摘要：最牛逼的高数和线代教程分享给你 。

最近在学习机器学习，涉及到不少高数和线代知识，大一学了这两门课，没怎么学懂，考试只是低空飘过，一直不怎么喜欢这两门课，开心直到现在都没再接触过。近期不得不重新捡回来，很是头大，毕业当废纸论斤卖掉的课本，在网上又高价买了回来。

快速过了一遍当初的教材，感觉依然是「知道怎么回事，但不理解为什么」，这一方面归结于自己领悟能力差，另一方面就要吐槽国内的教育理念了，教材不人性，老师教法也有问题。记得当时教线代的是一位刚博士毕业不久的老师，喜欢自 High ，经常在黑板上手推公式，推到最后自己都不会了，站在那儿傻乐，台下早已睡到一片。

曾一直认为学高数、线代，上面这两本教材是最好的选择，直到后来看了别人推荐的国外课本，才发现原来最好的教材在国外，后悔不已，为什么当初学的时候没有用到国外的教材，这之中的原因就不细说了。

下面就推荐我认为入门学习高数、线代最棒的教材和视频。

教材

没有打任何广告，单纯就是觉得这两本书不错，甩国内教材不知道几条街，文末会提供电子书，入门机器学习，看这两本就够了。

下面，是重头戏。推荐一个学习高数、线代最棒的入门视频，如果你有被它们支配过的恐惧，那绝对该看看，因为它会颠覆你的三观。

视频

这一系列视频教程是一位斯坦福大学的数学系学生 Gran 制作的，可以靠颜值吃饭非要靠才华，教程发布在油管的「3BlueBrown」频道上，也搬运到了国内的 B 站上。课程最大特点是通过 Python 制作的各种酷炫动画，帮助你理解深奥的数学概念，重塑你对高数线代的基本直觉，如果说国内老师教你「是什么」，Gran 则教你「为什么」。

比如，x 的立方求导，你知道为什么等于 3x 的平方么？

换个角度再来理解下：

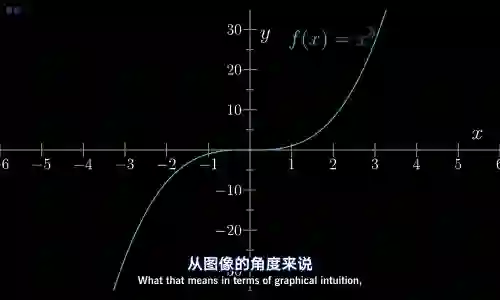
Sin(x) 求导为什么等于 Cos(x)？

除此之外，高数部分还有很多其他内容，微分、积分、泰勒级数这些。

再来看看线性代数，最头疼的莫过于矩阵、行列式相关的运算和各种性质了，但 Gran 很好地帮你理解这些问题。

比如，矩阵的运算，最正确地理解是把它当成一种特定的空间变换。

对于行列式，一直觉得就是一堆数字倒来倒去地计算，其实更好的理解也是放到空间中去。

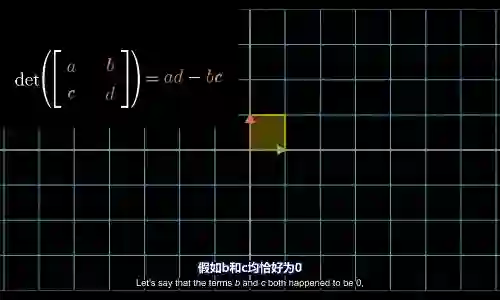
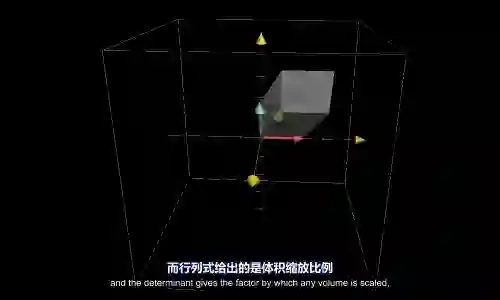
怎么样，有没有觉得你大学上的是假的高数和线代？

以上只是这门系列课的冰山一角，还有很多有意思的内容，可以到 B 站上看看，传送门：

https://space.bilibili.com/88461692/video

系列课很短，两三个小时就能看完，时间短不代表内容少，实际上内容非常丰富，你可能需要经常暂停下来思考一下，慢慢就会颠覆你此前对高数线代的认知。光看视频可能不够，我在 GitHub 上找到了热心网友做过的笔记，感兴趣的话可以 Star 一下：

∞ 3Blue1Brown 教程笔记

另外，如果你对视频中酷炫动画感兴趣，想学学看，作者提供了源码，可以试试看，仓库地址：

https://github.com/3b1b/manim

动画制作教程：

https://www.bilibili.com/read/mobile/17444

最后，老规矩，为了更方便你，我下载了高数和线代两门课的视频教程以及文章中两本教材的电子书，如需，可以在公众号后台回复：0032 得到。

本文完。

---

●编号787，输入编号直达本文

●输入m获取文章目录

推荐↓↓↓

算法与数据结构

更多推荐《25个技术类公众微信》

涵盖：程序人生、算法与数据结构、黑客技术与网络安全、大数据技术、前端开发、Java、Python、Web开发、安卓开发、iOS开发、C/C++、.NET、Linux、数据库、运维等。