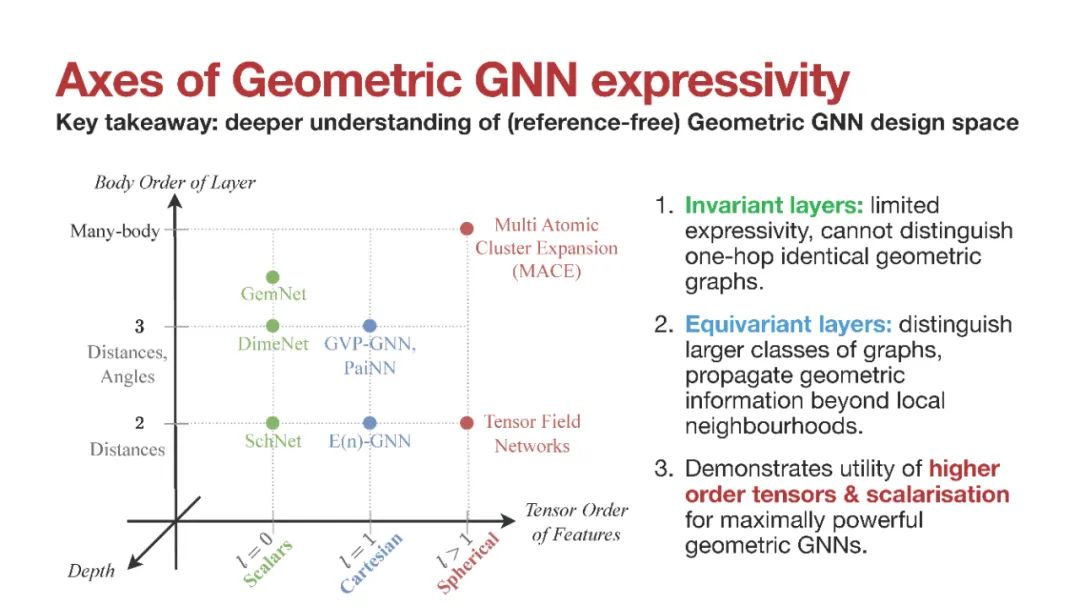
几何图神经网络表达能力如何？剑桥大学Chaitanya K. Joshi讲授《几何图神经网络》，附Slides与视频

通过Weisfeiler-Leman (WL)图同构测试，对图神经网络(GNN)的表达能力进行了广泛的研究。然而，标准GNNs和WL框架不适用于嵌入欧氏空间的几何图，如生物分子、材料和其他物理系统。在这次研讨会上，Chaitanya K. Joshi将分享最近的一篇题为“On the Expressive Power of Geometric Graph Neural Networks”的论文，他和团队提出了一个几何版本的WL测试(GWL)，用于在尊重潜在物理对称性的同时区分几何图形:排列、旋转、反射和平移。他们使用GWL来描述几何GNN的表达能力，这些GNN在区分几何图方面对物理对称性不变或等变。他将通过解释GWL如何揭示关键设计选择影响几何GNN表达能力的方式来结束演讲:(1)不变层的表达能力有限，因为它们无法区分单跳相同的几何图形;(2)等变层通过传播局部邻域以外的几何信息来区分更大的一类图;(3)高阶张量和标量化使最大强大的几何图神经网络成为可能;(4) GWL的基于判别的视角等价于泛逼近。可以在https://github.com/chaitjo/geometric-gnn-dojo上找到补充其结果的合成实验。

Chaitanya K. Joshi是剑桥大学计算机实验室的博士生，导师是Pietro教授Liò。他的研究探索了几何深度学习和图神经网络的交叉，用于建模分子，蛋白质和生化系统。此前，他是A*STAR信息通信研究所(I2R)的研究工程师，并获得国家科学奖学金(博士)。在此之前，他于2019年以致告别词的身份毕业于新加坡南洋理工大学(NTU)，获得计算机科学学士学位。

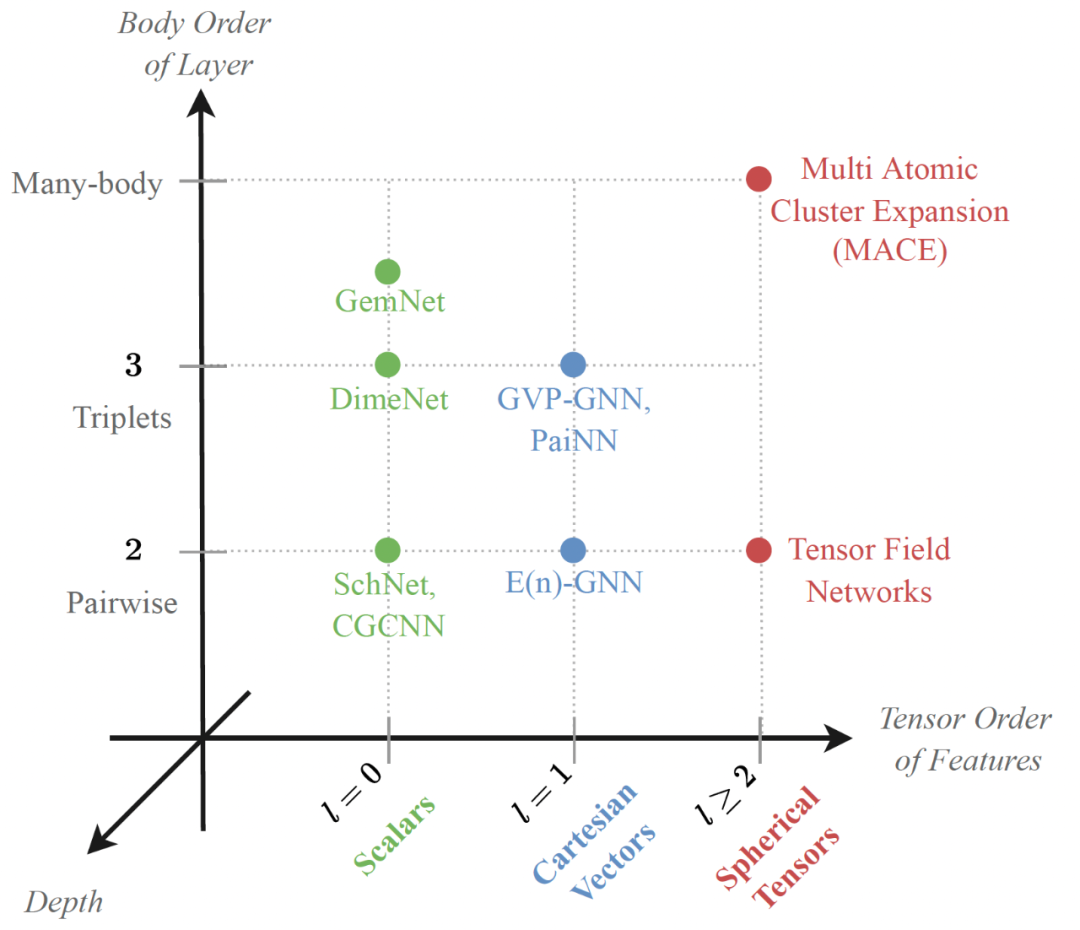
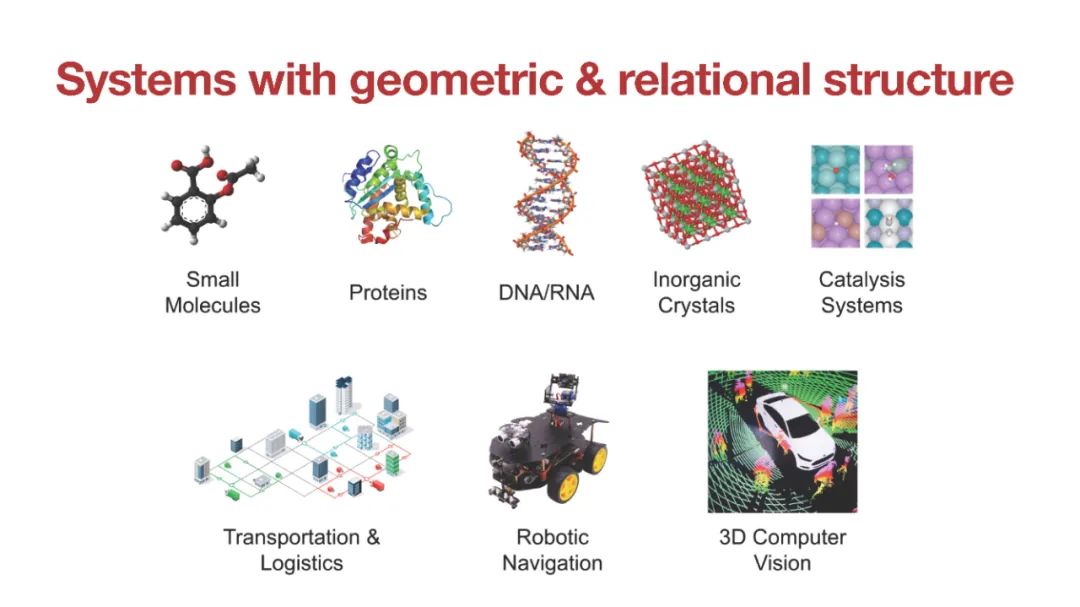
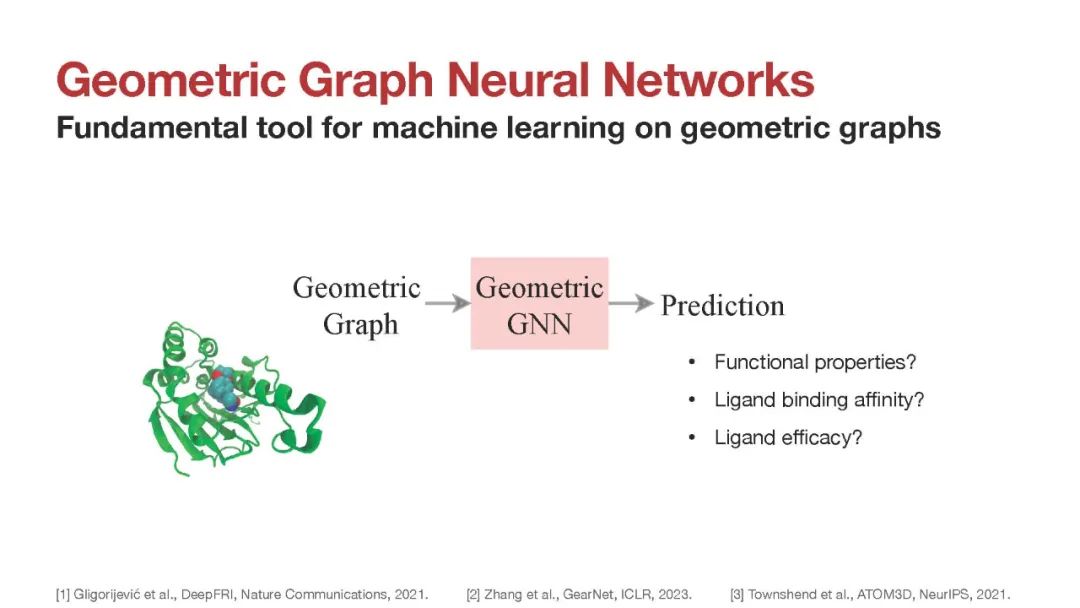
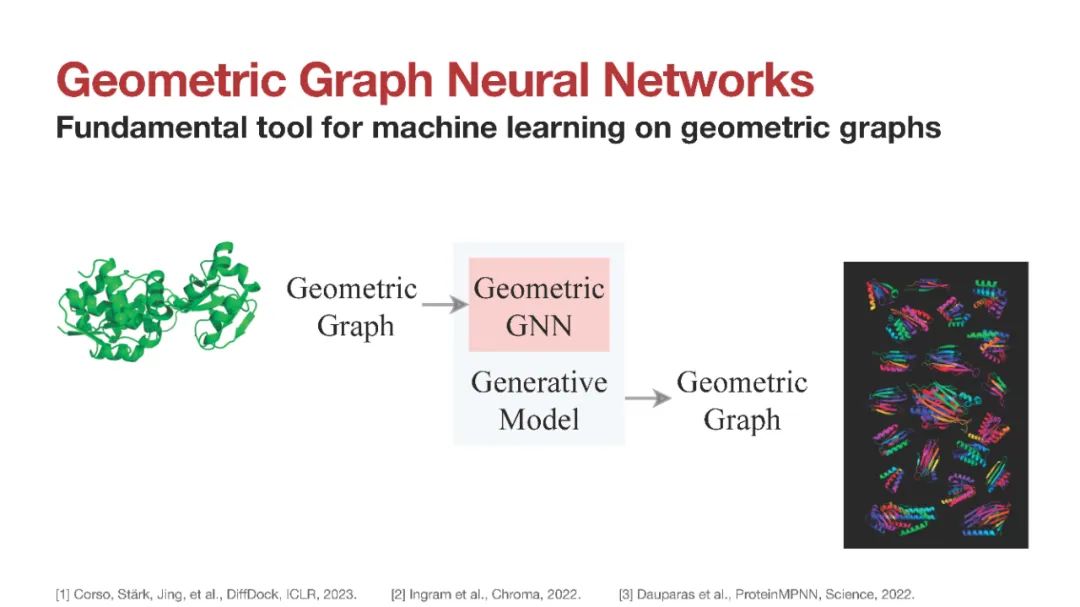
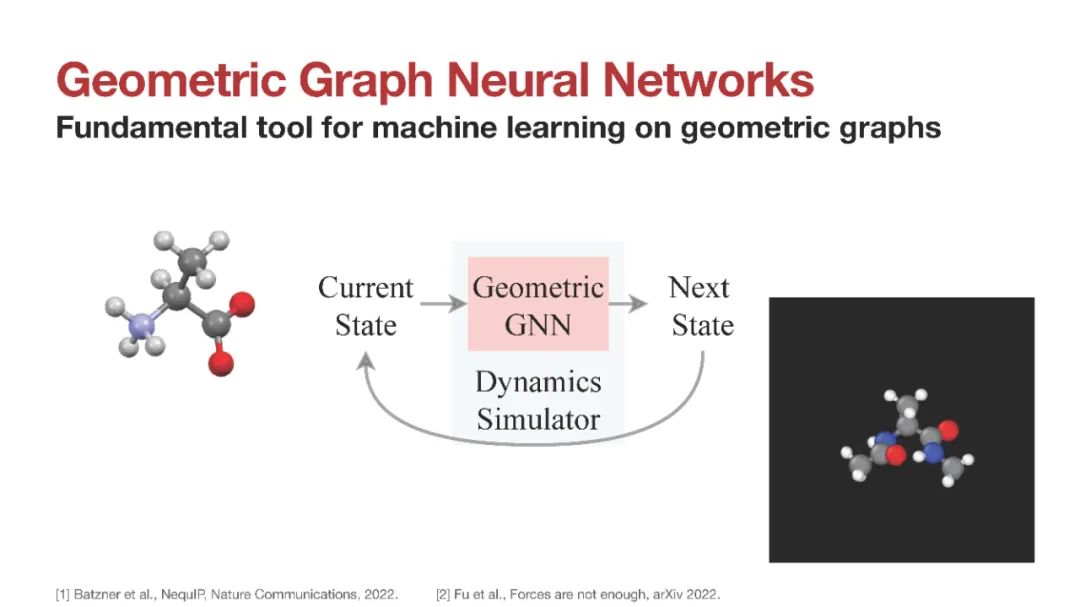
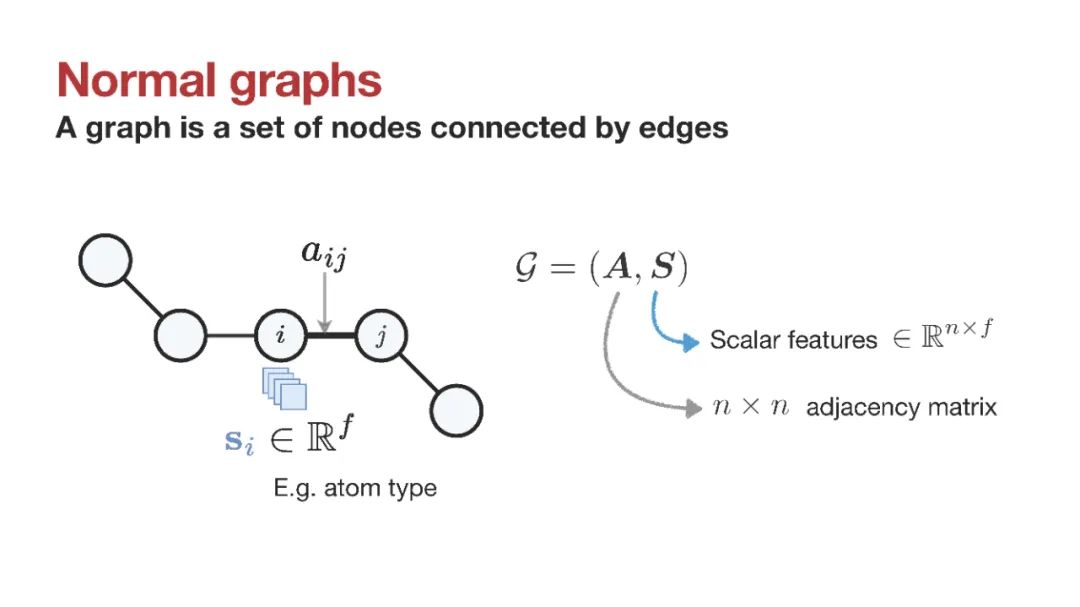
几何GNN表达力轴:该框架有助于形式化和理解几何GNN的设计空间，包括:(1)如何使用体序消息传递建立表达力强的局部邻域指纹;(2)高阶张量如何帮助确定邻域方向;(3)深度在几何信息传播中的作用。生物化学[1]，材料科学[2]，物理模拟[3]和多智能体机器人[4]中的系统包含几何和关系结构。这样的系统可以通过嵌入在欧几里得空间中的几何图进行建模。例如，分子被表示为一组节点，其中包含每个原子及其3D空间坐标以及其他几何量(如速度或加速度)的信息。值得注意的是，几何属性随着系统的欧氏变换而变化，即它们对旋转、反射和平移的对称群是等变的。没有考虑空间对称性的标准图神经网络(GNN)不适合几何图，因为几何属性将不再保留其物理意义和转换行为[5,6]。

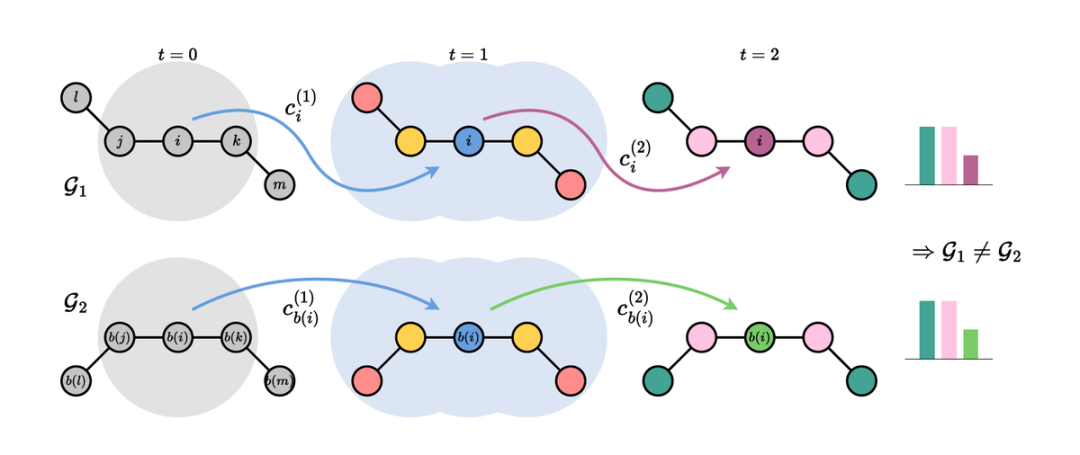
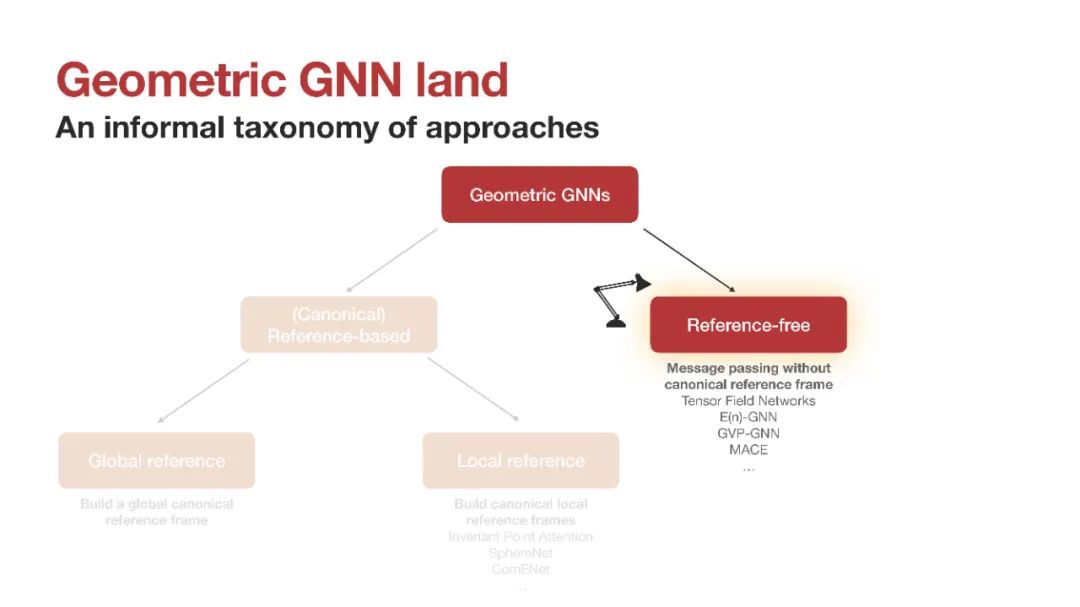
专门用于几何图的GNNs遵循消息传递范式[7]，其中节点特征通过聚集本地邻居的特征以排列等变的方式更新。至关重要的是，除了排列之外，节点的更新几何特征保留了初始属性的转换行为，即它们对旋转(SO(d))或旋转和反射(O(d))的李群也是等变的。我们用G作为这些李群的一般符号。我们考虑两类几何GNNs:(1) G-等变模型，其中中间特征和传播的消息是等变的几何量，如向量[8-10]或张量[11-13];(2) G 不变模型，仅传播局部不变的标量特征，如距离和角度[14-16]。这两类结构在蛋白质设计[17,18]、分子动力学[19,20]和电催化[21,22]等应用中都显示了有希望的经验结果。同时，关键理论问题仍未得到解答:(1)如何刻画几何图神经网络的表达能力?(2) G等变和G不变GNN之间的权衡是什么?用于区分非同构图的图同构问题[23]和Weisfeiler-Leman (WL)[24]测试已经成为分析非几何GNN表达能力的有力工具[25,26]。WL框架一直是图表示学习进展的主要驱动力[27-31]。然而，WL并不直接应用于几何图，因为它们表现出更强的几何同构概念，说明了空间对称性。