重磅！《几何深度学习》2022课程发布！帝国理工/DeepMind等图ML大牛共同讲授: 从图几何到深度学习

【导读】DeepMind-Petar Veličković和伦敦帝国理工学院教授Michael Bronstein等人讲授了关于几何深度学习的课程，讲述了一系列几何深度学习研究要点。非常值得关注！

重磅！《几何深度学习》新书发布，帝国理工/DeepMind等图ML大牛共同撰写，160页pdf阐述几何DL基础原理和统一框架

作为非洲机器智能硕士课程(AMMI 2021)的一部分，我们提供了一门关于几何深度学习(GDL100)的课程，它紧跟我们的GDL原型书的内容。我们使所有的材料和课件从这门课程公开可用，作为我们的原型书的同伴材料，以及一种方式深入到一些内容的未来迭代的书。

几何深度学习是从对称性和不变性的角度对广泛的ML问题进行几何统一的尝试。这些原理不仅是卷积神经网络的突破性性能和图神经网络的近期成功的基础，而且还为构造新型的特定于问题的归纳偏差提供了一种有原则的方法。

深度（表示）学习领域的现状让我们想起了19世纪的几何情况：一方面，在过去的十年中，深度学习在数据科学领域带来了一场革命， 以前认为可能无法完成的许多任务-无论是计算机视觉，语音识别，自然语言翻译还是alpha Go。另一方面，我们现在拥有一个针对不同类型数据的不同神经网络体系结构的动物园，但统一原理很少。结果，很难理解不同方法之间的关系，这不可避免地导致相同概念的重新发明。

几何深度学习是我们在[5]中引入的总称，指的是最近提出的ML几何统一的尝试，类似于Klein的Erlangen计划。它有两个目的：首先，提供一个通用的数学框架以推导最成功的神经网络体系结构；其次，给出一个建设性的程序，以有原则的方式构建未来的体系结构。

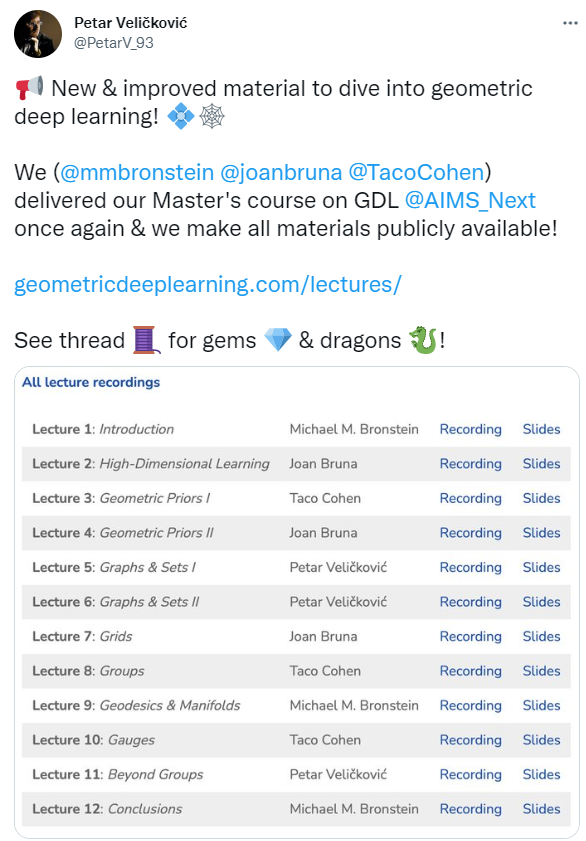
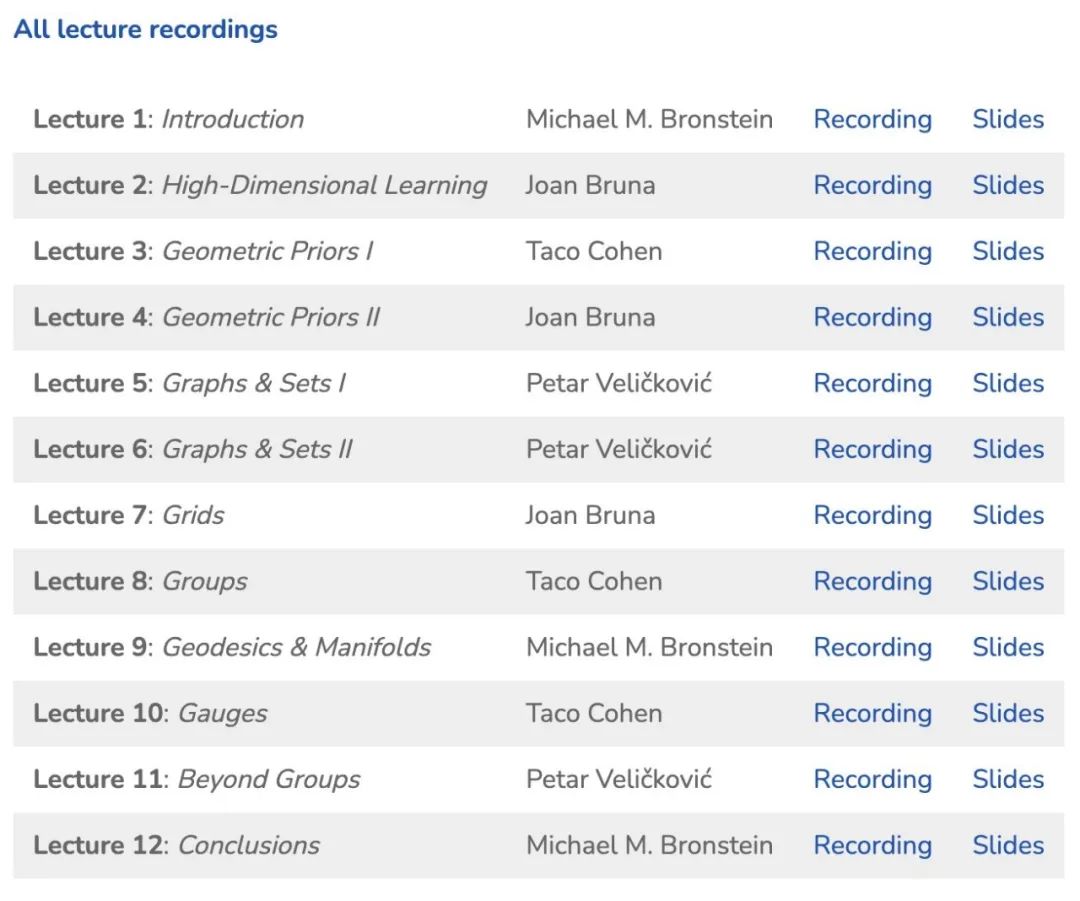
https://geometricdeeplearning.com/lectures/

第一讲视频

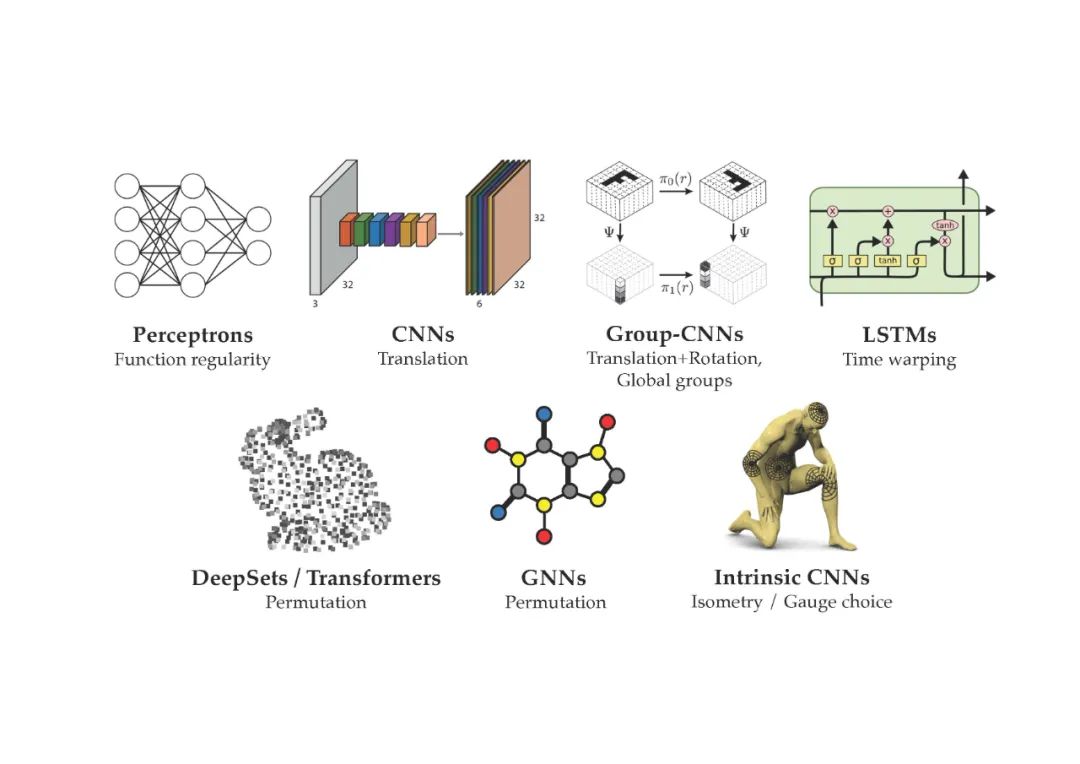
• 我们研究了流行的深度学习架构(CNNs, GNNs, transformer, LSTMs)的本质，并意识到，只要有一组合适的对称，我们就可以等价它们，它们都可以用一个通用的几何框架来表达。

• 更进一步，我们在一些不太标准的领域(如同质群和流形)上使用了我们的框架，这表明框架可以很好地表达这些领域的最新进展，如球形CNN, SO(3)-变换器，和规范-等变网格CNNs。

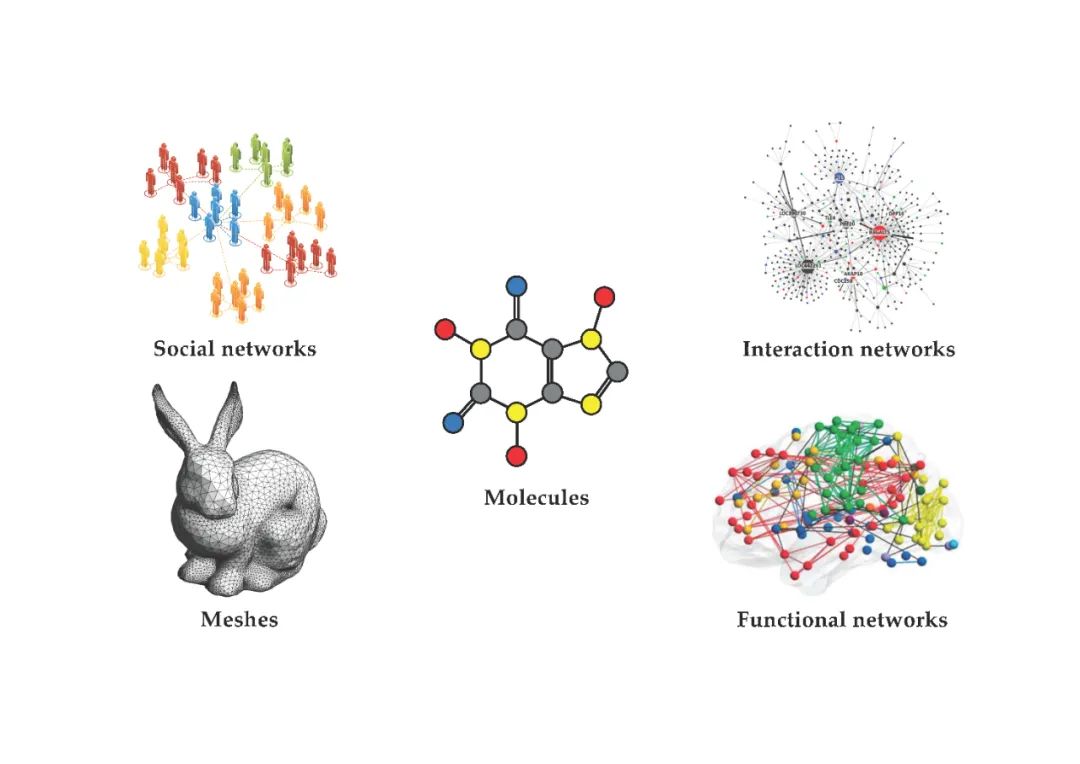
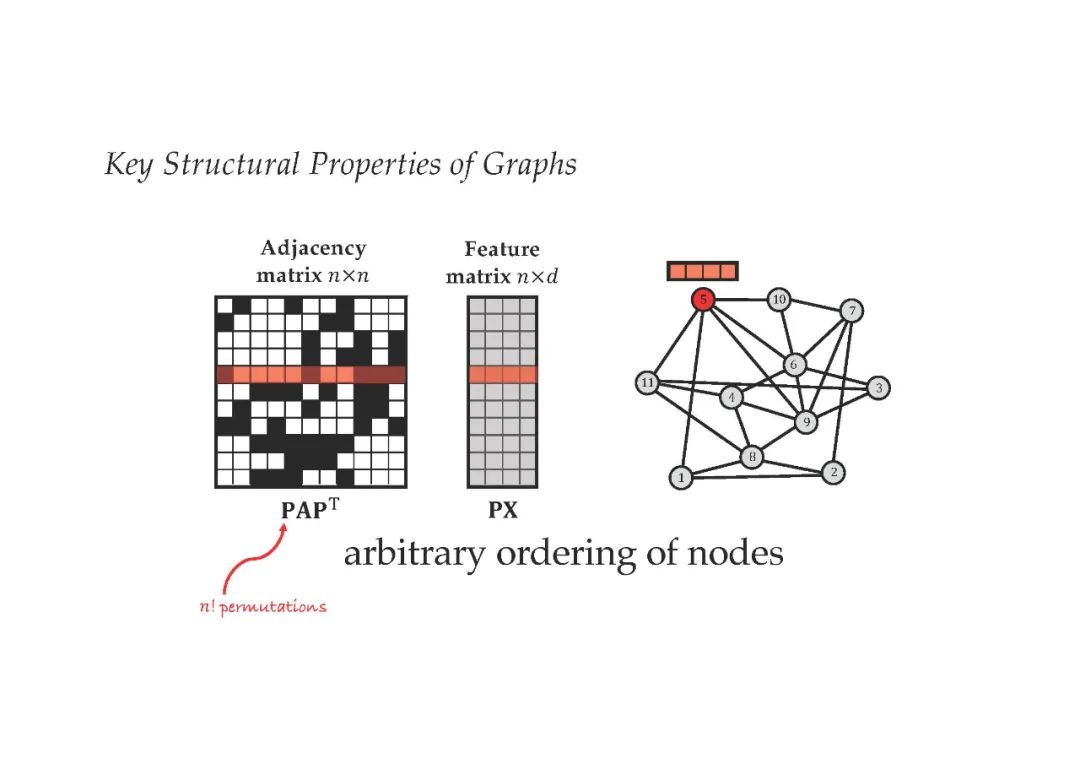
• 几何深度学习的“5G”:网格、组(具有全局对称性的齐次空间)、图(以及作为特定情况的集)和流形，其中几何先验通过全局等距不变(可以用测地线表示)和局部规范对称来表现。

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“GEDL” 就可以获取《重磅！《几何深度学习》2022课程发布！帝国理工/DeepMind等图ML大牛共同讲授: 从图几何到深度学习》专知下载链接

专知，专业可信的人工智能知识分发 ，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取5000+AI主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程资料和与专家交流咨询！

点击“ 阅读原文 ”，了解使用 专知 ，查看获取5000+AI主题知识资源