下一代图神经网络是什么？几何深度学习，大牛Max Welling教授视频讲解

阿姆斯特丹大学Max Welling教授为你讲解图神经网络发展趋势

Max Welling教授是阿姆斯特丹大学机器学习研究主席和高通公司技术副总裁。他还被任命为加拿大高级研究所(CIFAR)的高级研究员。他是“Scyfer BV”的联合创始人，该公司是深度学习领域的大学子公司，于2017年夏天被高通收购。在过去，他在加州理工学院(98- 00)，伦敦大学学院(00- 01)和多伦多大学(01- 03)担任博士后。他于1998年在诺贝尔奖得主g.t Hooft教授的指导下获得博士学位。Max Welling 2011-2015年担任IEEE TPAMI副主编(影响因子4.8)。自2015年(机器学习领域最大的会议)以来，他担任NIPS基金会的董事会成员，2013年和2014年分别担任NIPS项目主席和一般主席。他也是2009年AISTATS和2016年ECCV的项目主席，以及2018年MIDL的总主席。他曾在JMLR和JML的编委会任职，并担任神经计算、JCGS和TPAMI的副编辑。他获得了来自谷歌，Facebook, Yahoo, NSF, NIH, NWO和ONR-MURI的多次资助，其中NSF在2005年的职业资助。他是2010年ECCV Koenderink奖的获得者。Max Welling是阿姆斯特丹数据科学研究中心的董事会成员，他主管阿姆斯特丹机器学习实验室(AMLAB)，并共同指导高通- UvA深度学习实验室(QUVA)和博世- UvA深度学习实验室(DELTA)。Max Welling在机器学习、计算机视觉、统计学和物理学方面发表了超过250篇科学论文，H指数为62。

https://staff.fnwi.uva.nl/m.welling/

Graph Nets: The Next Generation - Max Welling

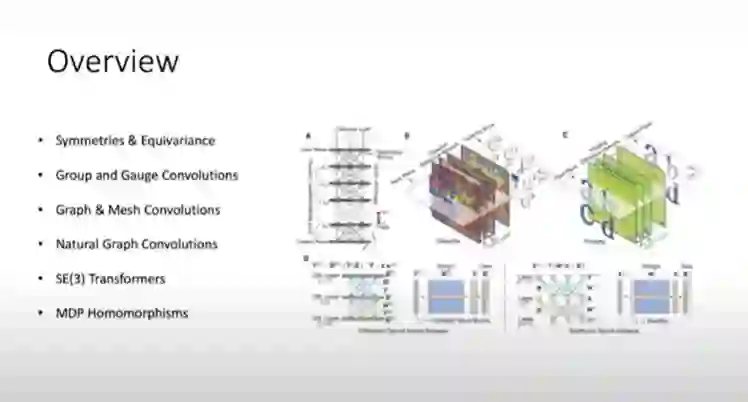
在这次演讲中，我将介绍下一代的图神经网络。GNN具有对图中节点的排列和图的整体旋转不变的特性。我们认为这是不必要的限制，在这次谈话中，我们将探索这些GNN的扩展，以更灵活的等变结构。特别地，一般图的自然图网络在节点排列下是全局等变的，但仍然可以通过本地消息传递协议执行。我们在流形上的mesh-CNNs在SO(2)规范变换下是等变的，因此，与常规的GNN不同，它具有非各向同性的核。最后，我们的SE(3)转换器是局部消息传递GNN，对排列不变性，但对全局SE(3)变换是等价的。这些发展清楚地强调了几何和对称作为图(或其他)神经网络设计原则的重要性。

https://video.ias.edu/machinelearning/2020/0721-MaxWelling

几何深度学习

很多数据不是序列和欧几里得分布的，而是球面图网络分布，那如何使用卷积在这些数据结构上？