【伯克利】神经网络中的对称性与同变性，附视频与114页ppt

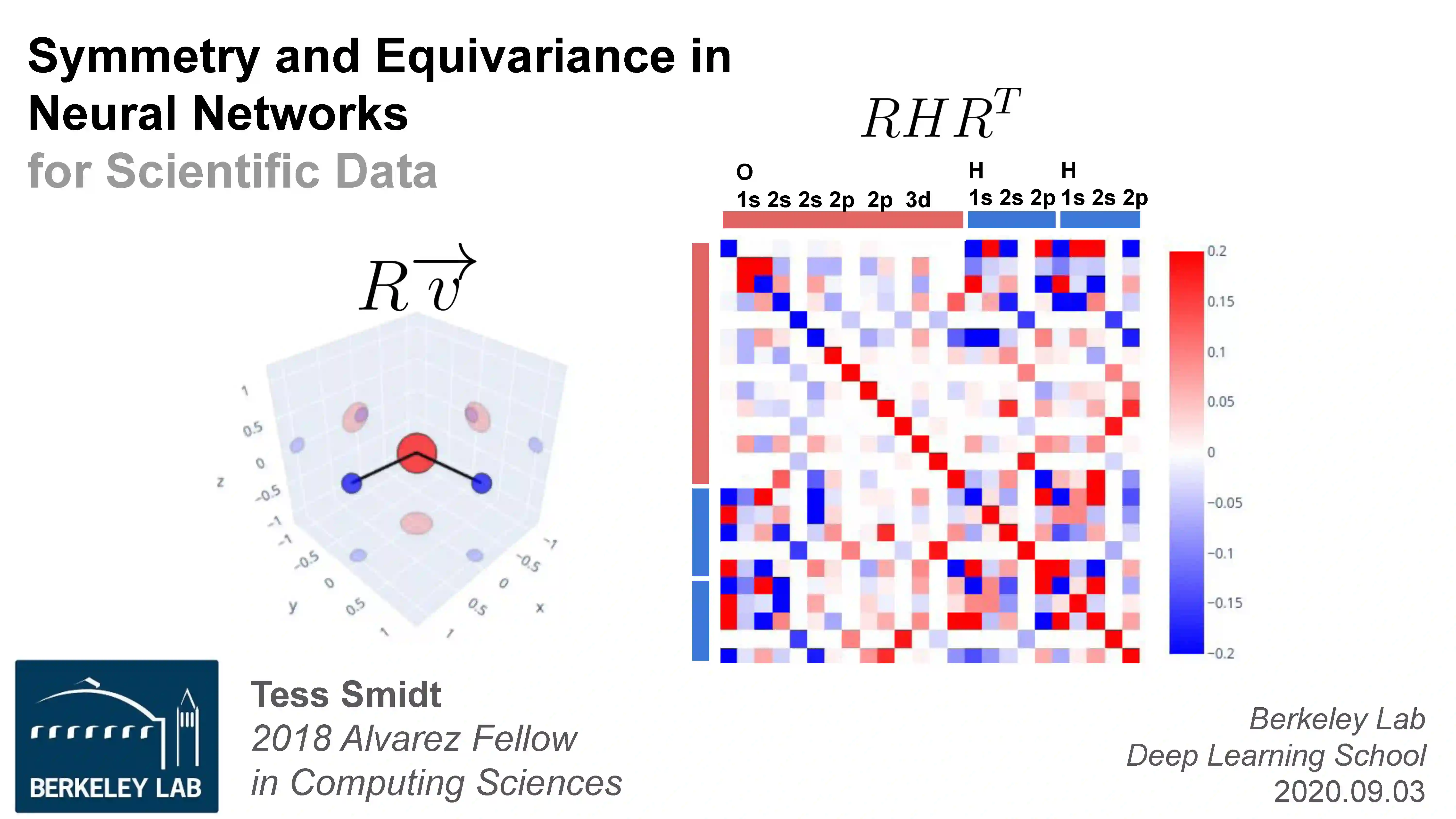
神经网络中的对称性与同变性

对称可以以多种形式出现。对于三维的物理系统，我们可以自由选择任何坐标系，因此任何物理属性都必须在欧几里得对称的元素下(三维旋转、平移和反演)可预见地变换。对于涉及图的节点和边的算法，我们在计算机内存中节点和边的排列情况下具有对称性。除非另外编码，机器学习模型不会对一个问题的对称性做出任何假设，并且会对坐标系统的任意选择或数组中节点和边的排序非常敏感。在机器学习模型中明确处理对称的主要动机之一是消除对数据增强的需求。另一个动机是，通过将对称编码到方法中，我们可以保证即使模型没有对“对称等效”示例进行明确训练，但模型对一个示例和一个“对称等效”示例会给出“相同”的答案。在这节课中，我们将讨论几种使机器学习模型“对称感知”的方法(例如输入表示、丢失和模型架构)。我们将集中讨论如何在神经网络中处理三维欧几里得对称和置换对称，描述这些对称的非直观和有益的结果，并讨论如何建立与你的对称假设一致的训练任务。

https://dl4sci-school.lbl.gov/tess-smidt