ICML 2024 | 如何在含有隐变量的环境中识别因果关系？

关键词**：**因果发现 代理变量 不可观测的混淆因子

导 读

本文是对发表于机器学习领域顶级会议 ICML 2024 的论文 Causal Discovery via Conditional Independence Testing with Proxy Variables 的解读。该论文由北京大学王亦洲课题组和复旦大学孙鑫伟助理教授合作完成，第一作者为北京大学博士生刘鸣洲。

本文提出了一种基于代理变量（Proxy Variable）的条件独立性检验方法，为从含有隐变量的环境中识别因果关系提供了理论保证。本文所述的方法在仿真数据集和败血症用药有效性分析中得到了验证。 论文链接：

https://arxiv.org/abs/2305.05281 开源代码：

https://github.com/lmz123321/proxy_causal_discovery 现场交流：

Poster Session 5 Hall C 4-9 #1707 Thu 25 Jul 17:30 p.m. - 7 p.m.

01

方法概览

区分因果关系与相关关系是许多科学研究中的根本问题，例如经济学、医学和通用人工智能。因果关系消除了混淆因子、中介因子等引入的伪相关，因而能帮助我们做出更可靠的决策。

在因果充分性假设（即环境中不含未观测的隐变量）下，因果发现可以通过检验条件独立性的方法来判断因果关系是否存在。然而，当环境中存在隐变量时，这一方法不再准确。这是由于我们无法收集隐变量的数据、也无法对其进行干预。因此，我们无法消除隐变量中的混淆因子、中介因子等引入的伪相关性。

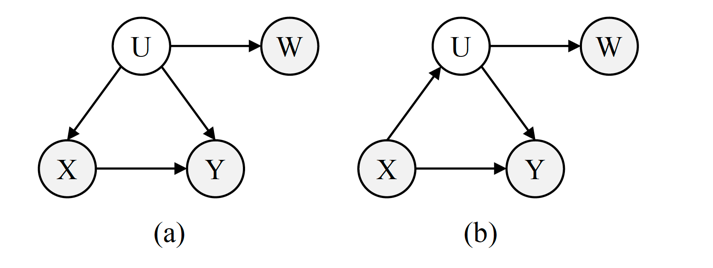
为了解决这一问题，Pearl 等人[1]引入了代理变量（图1）的概念。通常，代理变量可以是对隐变量的一种含噪声观测、或是隐变量的可观测后代。通过代理变量，我们可以调整隐变量引入的伪相关性，从而实现可识别性。然而，Pearl 等人[1] 和 Miao 等人[2,3]提出的代理变量调整方法局限于离散变量、或依赖于很强的参数化假设，限制了代理变量的应用。

图1：基于代理变量的因果发现。目标为判断 是否为 的因， 表示隐变量， 表示 的代理变量。图 (a) 和图 (b) 分别表示隐变量 是一个混淆因子和一个中介因子的情形。本文的方法不仅限于这些因果图，而是适用于任何满足 的情况。

本文提出了一中基于代理变量的假设检验，可以在不依赖参数化假设的情况下，识别连续变量之间的因果关系。具体来说，本文的策略是寻找一种恰当的离散化方法，使得被离散变量之间的概率矩阵在零假设下满足一个线性方程组。该方程组的系数向量（Coefficient Vector）是可识别的，因而，我们可以通过线性回归的残差的大小来判断零假设是否成立。为了实现这一目标，我们首先引入了一个离散化过程，该过程能确保离散后变量之间的概率矩阵满足满秩约束，进而保证线性方程系数向量的可识别性。其次，我们分析了离散化过程引入的误差。在平滑性条件下，我们说明这一误差可以被控制到任意小。最后，基于上述分析，我们提出了一个基于线性回归残差的假设检验统计量，并分析了渐进意义下假设检验的显著性水平和检定力。

最后，本文指出了所述方法在时间序列因果发现中的一种应用，即可以利用未观测时间变量的可观测后代作为其代理变量，实现对时间序列因果图的识别。该结论是项目组 NeurIPS 2023 论文Causal Discovery from Subsampled Time Series with Proxy Variables 的一部分。

02

背景介绍

**问题设定。**我们考虑判断两个变量 和 之间的因果关系。系统中还存在一个不可观测的隐变量 ， 可以是 和 之间的充分混淆因子或中介因子。在这种情况下，由于 引入的偏移， 和 之间的因果关系是不可识别的。为了调整这一偏移，我们假设 有一个代理变量 满足 。在实际情景中， 可以是 的含噪声观测或者其可观测后代。图1进一步解释了 之间的关系。

在 Markovian 和 Faithfulness 条件下，识别 和 之间的因果关系可以等价地转换为利用代理变量 检验以下的因果零假设： 接受零假设 说明因果关系不存在，而拒绝零假设则说明存在因果关系。

值得注意的是，我们的方法能够判断 和 之间是否存在因果关系，因果关系的指向则可以通过先验知识如时序关系、无有向环约束，或其他性质如不对称性、稳定性获得。

**Miao 等人[2]所述的方法。**对于离散变量，Miao 等人提出了一种基于代理变量 的假设检验过程。具体来说，他们将零假设 与以下的线性方程联系起来：其中 是响应向量， 是设计矩阵， 是系数向量。

这种联系是由于通过假设矩阵 满秩以及 可逆，在零假设下，公式 (1) 描述的线性系统成立且系数向量可识别。因此，可以通过观察线性回归的残差来判断零假设是否成立。

尽管上述方法已被证明对离散变量是有效的，如何将其推广到连续变量是一个困难的问题。这是由于公式 (2) 依赖的条件独立性在离散化后可能不再成立。此外，为了保证系数向量的可识别性，我们应该设计一个恰当的离散化过程使得 在离散化后仍保有满秩特性。我们将在后文中逐一具体解决这些问题。

03

方 法

• 本章中的假设、示例、命题等编号均对应原文。

在本章中，我们介绍一种基于离散化的假设检验流程。这一流程的核心是寻找一种离散化方法来建立公式 (1) 的可识别性。

为了实现这一目标，我们首先引入一种离散化方法，该方法在完备性条件（Completeness）下可以保证离散化后变量 和 满足矩阵秩的约束。其次，我们分析了离散化可能引入的误差。在平滑性条件下，我们说明这些误差可以通过细致的离散化被控制到任意小。基于上述理论，我们引入一个统计量进行假设检验，并分析了其显著性水平和检定力。

基于完备性的离散化

我们首先介绍一种离散化方法来建立公式 (1) 所需的可识别性。该方法依赖于以下的完备性假设：

**假设 4.1（完备性）。**假设条件分布 和 是完备的，即对于任何有界函数 假设为了理解假设 4.1 对我们方法的作用，注意当 是离散变量时， 的完备性意味着条件概率矩阵 满秩，这满足了 Miao 等人方法的要求；当 是连续变量时，假设 4.1 确保了存在一种 的离散化 使得 行满秩。此外，结合 的完备性，还可以确保存在 的离散化 使得 可逆，这就建立了公式 (1) 所需的可识别性。

值得注意的是，假设 4.1 所描述的完备性被很多工作类似的采用[2,3]，它的成立基本上只要求结构方程中的外源变量有非零的描述函数。

**示例 4.2（满足完备性的加性噪声模型）。**假设 满足加性噪声模型（Additive Noise Model, ANM） ， ，其中 表示外源变量。如果 可逆且有非零导数，且 的描述函数非零，则条件分布 和 满足完备性。

在假设 4.1 下，我们证明可以找到一个离散化过程使得 行满秩、 可逆。

**命题 4.4。**假设 4.1 成立。则对于任何 的离散化 ，存在一个 的离散化 使得 行满秩。类似的，也存在 的离散化 使得 可逆。

受命题 4.4 的启发，我们提出算法 1 来具体的搜索满足矩阵秩约束的离散化，这一算法的设计原理请参见原文的介绍。

离散化误差分析

我们讨论离散化误差的控制问题。具体来说，我们说明在如下的平滑性假设下，可以通过细致的离散化将误差控制到任意小。

**假设 4.7（TV 平滑性）。**假设映射 和 相对于总差变距离（Total Variation Distance）是 Lipschitz 连续的，即存在 和 满足对任何 ，其中 。

为了理解假设 4.7 对于控制误差 的作用，注意到对于很小的离散格（Discretization Bin），假设 4.7 意味着距离很小。类似的，它还意味着距离很小。由于在零假设下，我们有 ，利用三角不等式，我们可以控制距离 从而控制误差项 。

值得注意的是，假设 4.7 在具有连续可导的结构方程的结构因果模型中均可成立，是一种比较弱的假设，具体的说明请参见原文的示例 4.8。

**命题 4.9。**假设 是一个紧的区间（Compact Interval）且 是 的一个分割满足则在假设 4.7 和零假设 下，对任何的 ，我们有从而离散化误差 可以被控制。

命题 4.9 说明在平滑性条件下，只要离散化格选取的足够小，就能将误差控制到任意小。此外，为了解决 是一个非紧集的情况，我们还引入了紧分布（Tight Distribution）的概念，具体的说明请参见原文的定义 4.10 和 命题 4.14。

假设检验

令 并令相应的极大似然估计器为 ，满足 令 表示回归 到 的最小平方法误差，我们采用平方误差 为我们的检验统计量。

**定理 4.15。**假设 4.1，4.7 成立，则在零假设下， 依分布收敛到卡方分布。因此，对于任意的显著性水平 ，即我们的假设检验过程有一致的显著性水平 。

**定理 4.18。**假设 4.1，4.7，4.16 成立，则对于任意 ，即我们的假设检验过程的检定力为 。

04

实 验

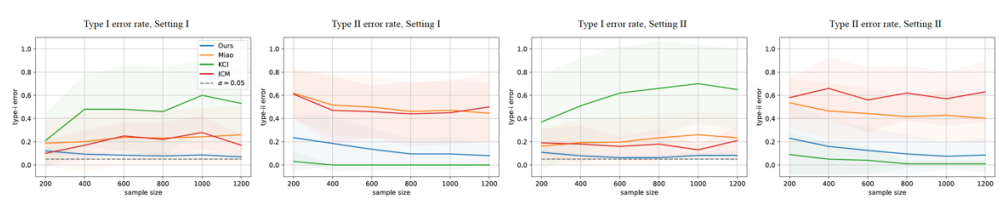
本文在图1所述的两种因果图上进行了仿真实验，结果说明本文的方法能实现一致的显著性水平和检定力。

图2. 不同样本量下假设检验的第一类和第二类错误率。对于一个正确的检验过程，第一类错误率应该接近显著性水平 （虚线），第二类错误率应尽可能接近零。

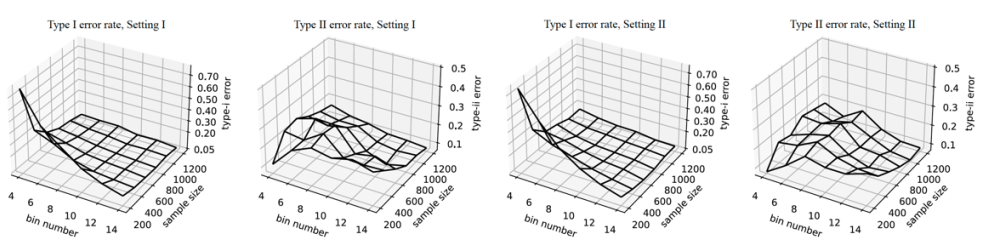
图3. 不同离散化粒度下假设检验的第一类和第二类错误率。

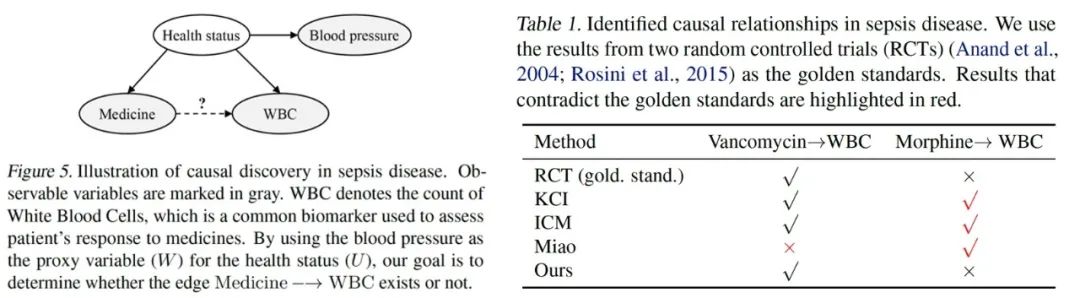
此外，本文还在败血症用药有效性问题上进行了实验，结果表明本文提出的方法能有效区分因果关系和隐变量带来的伪相关关系。

图4. 描述败血症的因果图以及各种方法的结果比较。

05

应用于时间序列因果发现

本文所述的基于代理变量的假设检验方法可以应用于时间序列因果图学习的问题中。具体来说，在时间序列中，每个未观测变量都存在一个可观测的后代（即该变量在未来某个可观测时刻的测量）。因此，我们可以利用这一可观测后代作为未观测变量的代理变量，对未观测变量引入的偏移进行调整。

图5. 利用代理变量区分直接因果效应（ ）和间接因果效应（ ），进而识别时间序列因果图。

参考文献

[1] Kuroki, M. and Pearl, J. Measurement bias and effect restoration in causal inference. Biometrika, 101(2):423–437, 2014. [2] Miao, W., Geng, Z., and Tchetgen Tchetgen, E. J. Identifying causal effects with proxy variables of an unmeasured confounder. Biometrika, 105(4):987–993, 2018. [3] Miao, W., Hu, W., Ogburn, E. L., and Zhou, X.-H. Identifying effects of multiple treatments in the presence of unmeasured confounding. Journal of the American Statistical Association, pp. 1–15, 2022.