ICLR2021 | 初探GNN的表示能力
-
论文标题:EXPRESSIVE POWER OF INVARIANT AND EQUIVARIANT GRAPH NEURAL NETWORKS -
论文地址:https://arxiv.org/pdf/2006.15646.pdf -
代码地址:https://github.com/mlelarge/graph_neural_net 作者:Waïss Azizian;Marc Lelarge 研究方向:GNN 表达能力
欢迎关注小编知乎:图子
GNN 表达能力的研究一直比较高深莫测的方向,刚入门的小白面对大量的数学公式和推导过程,肝完了还是不能明白其意义所在,心里出现了无数个小问号。但在我看来这个方向是实现从简单的使用GNN转变到深层次理解GNN的基石。莫慌,这篇文章会有大量的前置知识,以比较友好的方式带大家涉足 GNN 的表达能力,小编带你们:1)回答一条疑问,既然我们会使用 GNN了,那研究 GNN 的表达有啥实际意义?2)告诉大家 GNN 的表达能力是啥,通常用什么办法去衡量它;
0. ABSTRACT
多种图神经网络(GNN)在图结构数据的广泛应用。本文作者提出了一个理论框架实现比较这些 GNN 架构的表达能力。首次证明了GNN 的函数逼近保证,为更好地理解其泛化能力铺平了道路。论文的理论结果针对两类 GNN 框架:一类是不变图神经网络(invariant GNNs),用于计算图级别嵌入,输入图的节点的排列变化不影响输出结果;另一类是同变图神经网络(equivariant GNNs),用来计算节点嵌入,输入的排列变化会影响输出;论文表明FGNN 是迄今为止对给定阶数张量提出的表达能力最强的架构。实验在二次分配问题上验证了效果,达到比现有算法更好的平均性能。
1. 前置知识
GNN 的表达能力
1. 首先我们来聊聊为啥要探索 GNN 的表达能力?
考虑最熟悉的消息传递图神经网络,它的工作机制是在图结构数据上进行信息的传播和聚合,虽然利用了图数据的结构归纳偏置,然而它并非绝对的保留图结构信息。如果GNN仅仅具有使用特征信息的能力,而缺乏保持图拓扑结构的能力,那很可能会败给网络嵌入方法。因此我们通过思考现存 GNN 的能力和局限,就能够指引我们design更强大的 GNN。
2. “表达能力”这个词显得过于抽象了,问题来了,到底什么是表达能力?如何衡量 GNN 的表达能力?
本文主要从两个方面着手,来解释和衡量 GNN 的表达能力:
-
区分能力(separating power)
经典的方法就是论文《 How Powerful are Graph Neural Networks?》中使用的图同构检验。你设计的图神经网络强不强却决于它区分图同构性的能力,也就是说我们希望 GNN 具有很强的特征抽取能力,抽取的特征能够协助我们在隐空间中判定两个图是否同构。
-
逼近能力(approximation power)
此处参考博文[图神经网络的表达能力与置换同变性]中的解释,利用经典的函数逼近思路,即关心神经网络能够表达的函数的范围有多大,该方面最著名的结果是前馈神经网络的万能逼近定理。虽然GNN 相较于前馈神经网络又引入了图的拓扑信息,但是可以借鉴万能逼近定理的思想,探索 GNN 能够做到的全部事情的集合(GNN可以逼近的定义在图上的函数集合),即 GNN 的表达能力。
2. GNN 的区分能力与逼近能力
本文主要聚焦于探索 3 种 GNN 架构的表达能力:消息传递图神经网络(MGNN),k 阶线性图神经网络(k-LGNN),k 阶Folklore GNN(k-FGNN)。MPNN 是实践中最流行的GNN架构,它的层是局部的,因此在 GPU 上可高度并行化,这使得它们对大的稀疏图形具有可扩展性;而 k-LGNN 和 k-FGNN 将处理图表示的过程转换成处理 k 阶张量,这使得它们在k≥3的情况下实际用途很小。
GNN 的区分能力
作者比较了这些网络区分图同构问题的能力。而图同构问题通常被认为是 NP 问题,目前最有效的算法是 WL Test,因此将每一种网络架构的区分能力与 k-WL 像比较。已知 时, -WL 比 -WL 具有更强的区分能力,因此存在非同构图不能被 -WL区分但是可以被 -WL区分的情形。很多文献中通过证明 GNN 逼近 WL Test 的能力突出其表达能力。Xu 等人(2018)证明引入的GIN与2-WL一样强大;Maron(2019a)、Geerts (2020b)、Geerts (2020a)中,证明 k-LGNN 与 k-WL 一样强大,2-FGNN 与 3-WL一样强大。对于k阶张量的区分力,本文将 -FGNN 中的 推广到一个一般值,并证明 -FGNN 是本文中最强大的结构。
数学上表达:对于一对图 和 ,如果 -WL Test 判定其为非同构的 ,那么存在一个 -FGNN 有同样的能力判断它们的非同构性:。
GNN 的逼近能力
首先来说说 GNN 区分能力的局限性:判定GNN的区分能力需要对图数据进行成对比较:我们需要先验地为每对图提供不同的GNN,以便区分它们。这样的结果在实际的学习场景中没啥意义。
本文中的主要贡献是克服了这个问题,表明单一的GNN可以为所有图提供有意义的表示。作者描述了可以分别由MGNNs、k-LGNNs 和 k-FGNNs 逼近的函数集合。并表明在处理 k 阶张量的架构中,k-FGNNs 具有最佳的逼近能力。
Maron等人(2019b);Keriven & Peyré(2019);Chen(2019) 证明了 linear GNNs 中的万能逼近定理。他们表明,一些 GNN 可以逼近定义在图上的任何函数。为了能够逼近任何不变函数,需要定义非常复杂的网络,即 k-LGNN,其中节点数目为 n 时 k 趋向于无穷大;作者证明任何弱于 (k+1)-WL 的不变函数都可以由 k-FGNN 逼近,所以让 k 趋向于无穷大就意味着普遍性。k-FGNN 的普遍性结果是论文的另一个贡献
论文的第二组结果将以前的分析从不变函数扩展到同变函数。同变 GNN 与 不变 GNN 的概念是比较重要的,会在后面给大家讲解。目前关于同变GNN的研究比较少:Keriven & Peyré(2019)证明了线性同变GNN 的普遍性。本文作者考虑 k-WL 的同变扩展,并证明当 k≥1时,同变(k+1)-LGNNs 和 k-FGNN 可以逼近任何比同变(k+1)-WL弱的同变函数。
论文的 Outline
-
定义了本文中研究的各类 GNN,提供了关于 GNN 的重要理论,描述了每个 GNN 架构的 区分能力; -
给出了MGNNs、LGNNs 和 FGNNs 在固定张量阶数下的 逼近保证,同时涵盖了不变和同变的情况; -
在 NP-hard 图对齐任务中 验证了论文的理论结果。
Quadratic Assigment Problem (QAP) 的实验结果
为了验证论文的理论上的贡献,作者通过实验表明,2-FGNN 优于经典的 MGNN。Maron等人(2019a)已经提出了2-FGNN 的不变版本在图分类和图回归任务中的最优结果。本文考虑了图的对齐问题,并表明同变的 2-FGNN 学习的一个节点嵌入在很大程度上击败了其他算法。
3. 相关概念
符号表示
用来表示 (对于不同的 值)的任意有限维空间的特征, 中向量的乘积总是指分量级乘积。有两种方式看待带有特征的图:
1)图被作为 阶张量: , 时,图的(加权)邻接矩阵的经典表示是 中的一个 2 阶张量,这种情形允许将边上的特征 替换成 ;
2)用图的离散结构和一个附加的特征向量来表示:表示成 ,离散图集合 具有 个节点和边 ,边是无权重的,这样的 带有一个特征向量 表示一个带有顶点特征的图。
不变算子和同变算子
令 , 上的排列集合为 。对于 , ,我们定义 ,只要图 的节点数目为 , 中的排列和图 之间的 操作都是有效的,即它对任意图表示的 阶张量都有效。
有了图以及图上节点排列的概念,我们很容易引入图同构:如果图 拥有相同数目的节点并且存在一个排列 ,使得 ,那么 就是同构的。
同构想讲的是一个什么事呢?通俗的说,就是图 的全部顶点被映射到图 后,这些顶点可能标号变了,但是如果在“旧”的图中有的关系,在“新”图中依然保留,只不过是“位置”变了。
Definition 1
-
不变函数(invariant function):对于每一个排列 以及每一个图 ,如果 , 那么函数 就是不变的。
-
同变函数(equivariant function):对于每一个排列 以及每一个图 ,如果 ,那么函数 是同变的。
翻译成人话就是:置换不变性使得输出与输入顺序无关,而置换同变性使得输出顺序与输入顺序对应。将一个同变函数与一个不变函数组合会得到一个不变函数。
-
invariant summation layer:当阶数 时, ,对于 ,
也就是对一个图的不同排列进行求和操作。
4)equivariant reduction layer: ,
对于消息传递 GNN,作者使用了同变层 : , 表示成 ,其中 是一个可学习的参数。同时需要一个映射 将输入图转换成一个高阶张量, ,就是将给定图的每 个元组映射到其同构图的初始函数。
4. 定义 GNN
在本节中,作者定义了论文研究的各种 GNN 体系结构。在所有的体系结构中,有一个主要的构建块或一层将第 层图表示空间映射到 层图表示空间。作者为消息传递 GNN、线性 GNN 和 folklore GNN 定义三种不同类型的层。每种 GNN都有一个不变版本和同变的版本。所有的架构都将共享最后一个函数:在不变的情况下,函数为 ;在同变的情况下, ,它们都是连续函数。由于等变函数会和输入节点的顺序有关,因此它通常由多层感知器建模,并应用于图中每个组件,即节点级别的函数。
换句话说,每个网络将图 作为输入,在不变情况下产生 中的图级别的嵌入;在同变情况下产生 中的节点级别嵌入,然后这些嵌入分别通过函数 或 来获得 或 中的特征,用于学习任务。接下来我们针对具体的 GNN 来定义它们的不变和同变版本。
MESSAGE PASSING GNN
消息传递 GNN 的不变版本和等变版本集合定义如下:
其中, 是消息传递层。
LINEAR GNN
定义LINEAR GNN 的不变版本和等变版本集合如下:
对于 是线性等变层。
FOLKLORE GNN
定义 folklore GNNs 的不变版本和等变版本集合如下:
其中, 是同变函数,reduction 层 用于同变的情况,summation 层 用于不变的情况, 是 folklore 图层。
5. GNN 的理论结果
这一节作者提出了一些定理,推导每一种 GNN 的表达能力,最终表明 2-FGNN 是强大结构。
5.1 WEISFEILER-LEHMAN 的不变和同变版本
作者在被整数 参数化的图上引入了一组用于图同构问题的函数,并作用于 个顶点的元组。给定每个 -tuples 一个颜色 ,代表这个个元组中顶点的同构情况, -WL 测试依赖于以下邻域的概念,
给定一个顶点及其邻域信息:对于任意 , ,然后 -tuples 的颜色重置如下:,对于 ,函数 Lex 意味着所有出现的颜色都是按字典顺序排列的,并被自然数的初始段所取代。
不变 k-WL测试
对于一个图 ,令 -WL 表示第 次迭代 -WL 算法颜色的多集,经过有限的几步(取决于图中顶点的数量),算法就会停止,因为已经达到了稳定的着色(没有着色的 -tuples 被进一步划分)。用 -WL 表示稳定着色中的颜色多集。这相当于一个图的不变函数,通常被用于测试图是否同构。
同变 k-WL测试
为了表达同变架构的判别能力,定义一个同变版的k-WL测试。从标准k-WL算法给出的 -tuples 的着色中构建一个顶点的着色。从形式上看,定义: ,对于 , ,同样基于上面的算法定义稳定着色。
5.2 GNN 的区分能力
作者使用Timofte(2005)提出的等价关系来表征一组函数的区分能力。
定义 2.
是定义在一个集合 上的一组函数 ,每个函数在 上取值,集合 上的等价关系 如下:对于任意 ,
给定两个函数集合,如果 ,则 较 而言更有区分力。 和 中的所有函数都需要定义在同一个集合上,但可以在不同的集合中取值。
作者给出结论, -WL算法的同变版本比不变版本更具有区分力。测试的WL层次结构的一些属性可以用区分能力的概念来重新表述。特别是,Cai等人(表明, 区分能力严格高于 -WL ,简写为:
根据这种区分能力的概念,作者总结目前存在的 GNN 的区分能力如下:
Proposition 3.
对于 ,
对于 ,所有GNN都在处理2阶的张量,即处理图的邻接矩阵。如果2-FGNN是最复杂的架构,我们看到它在迄今为止提出的所有处理 2 阶张量的架构中具有最好的区分能力。
5.3 GNN 的逼近能力
对于 有限维空间,用 来表示从 到 的不变和同变连续函数的集合。 表示一类函数 的闭包 。下面的定理特别指出, -FGNN 可以逼近任何连续函数,在不变和同变情况下,其区分力小于 -WL。
定理4.
设 , 是紧凑集合。对于不变的情况,有:
对于同变的情况, 有:
在 时不变情况下,我们有
换句话说,2-FGNN 比其他处理 2 阶张量的架构具有更好的逼近能力。 Proposition 3 表明 2 -FGNN 是本文研究的那些处理阶为2的张量的最佳区分架构,定理4意味着其逼近能力也是如此。因此无论从区分力还是逼近能力来衡量,2-FGNN 都是最强的。
6. 实验
为了实验评估结果,作者研究了一个组合优化的经典问题二次分配问题, 对于 两个 对称矩阵来说,它包括解决
是 的排列矩阵的集合.很多优化问题可以被看作二次分配问题。例如网络对齐问题,它包括寻找以邻接矩阵表示的两个图之间的最佳匹配,很多baseline针对这个 NP-hard 问题展开过研究,但是结果表明,这些方法在规则图上会失败,规则图在图同构测试中特别困难的一类图.
为了弥补这一弱点,作者使用了 2-FGNN ,即 2-FGNN的同变版本,给定两个图,在 中为每个图产生一个嵌入,其中 是节点的数量,然后将其相乘,得到一个节点上的 的相似性矩阵。通过解决线性分配问题(LAP),最终计算出一个排列,并将此 的结果作为成本矩阵。作者在两个分布上测试了我们的架构:Erdós-Rényi模型和随机规则图。与以前的工作相比,匹配图的准确性有很大提高。
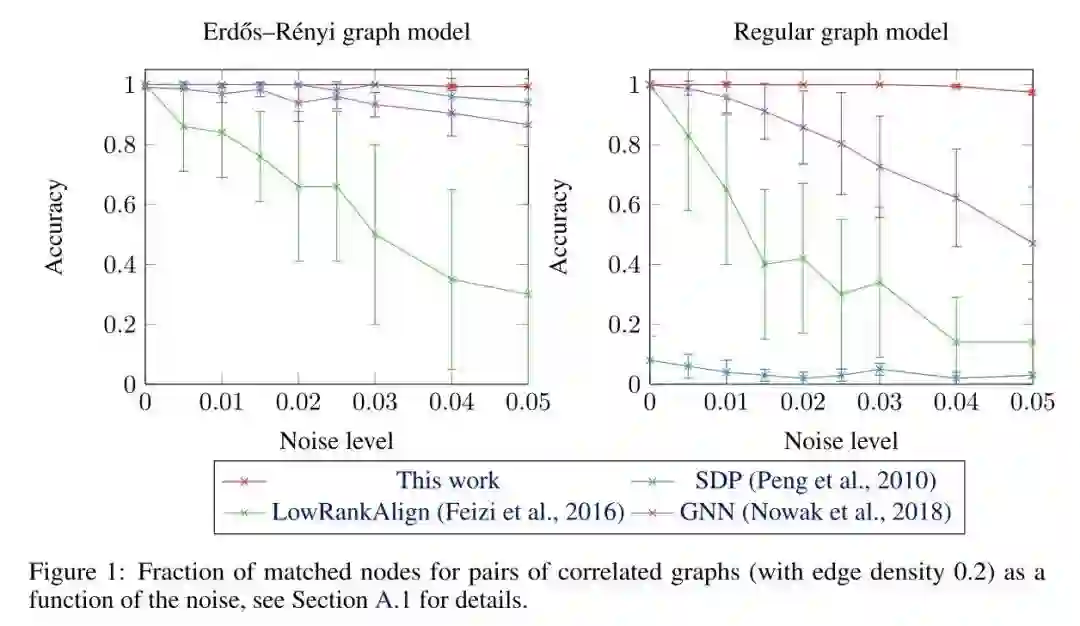
根据图1,可以看出本文给出的表达能力最强的 2-FGNN 的匹配准确率在两种图上都获得了最优效果。
Conclusion
论文推导了各种实用的GNN架构的表达能力:包括消息传递GNN、线性GNN和 folklore GNN,包括它们的不变和同变版本。作者表明所有处理2阶张量的GNN中,folklore GNN具有最好的逼近能力。从应用的角度来看,作者明了它们在QAP问题上的性能大幅提升。
专知便捷查看
便捷下载,请关注专知公众号(点击上方蓝色专知关注)
后台回复“GNNEP” 就可以获取《ICLR2021 | 初探GNN的表示能力》专知下载链接






