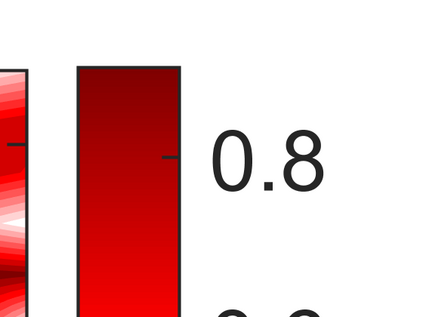
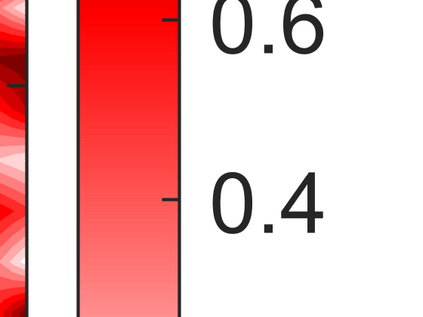
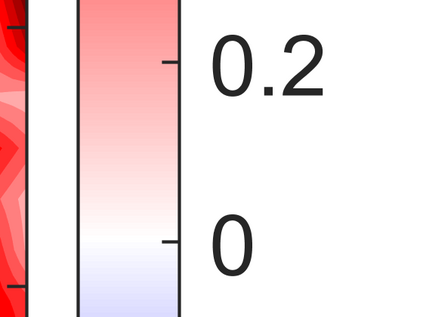
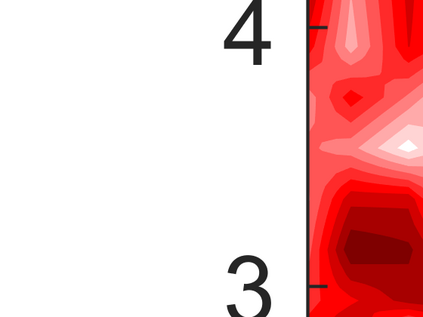
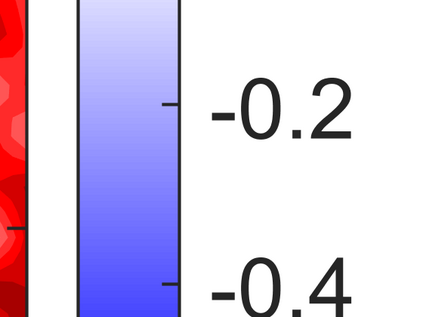
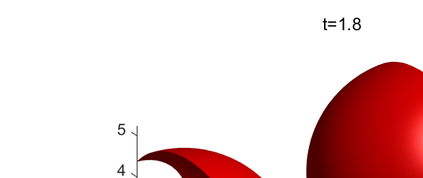
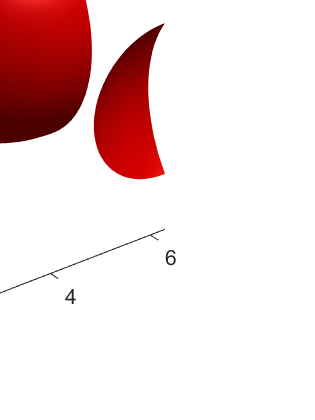
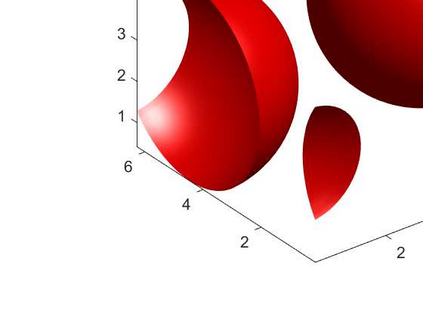
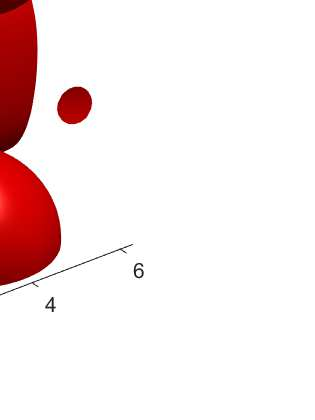
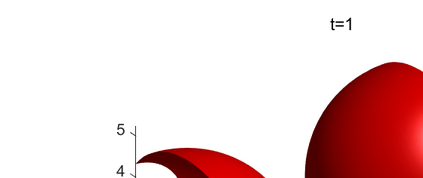
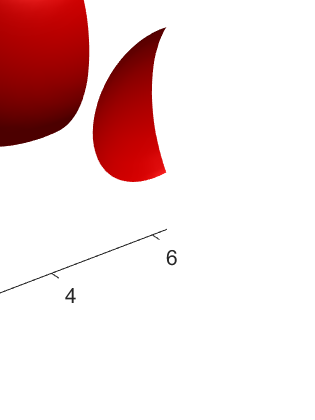
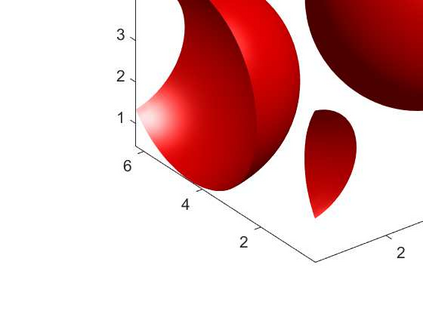
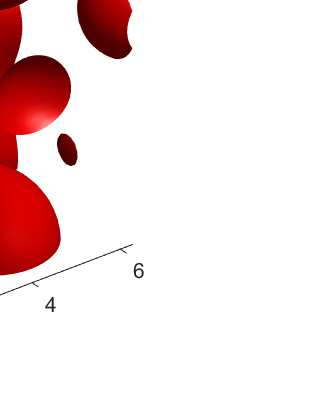
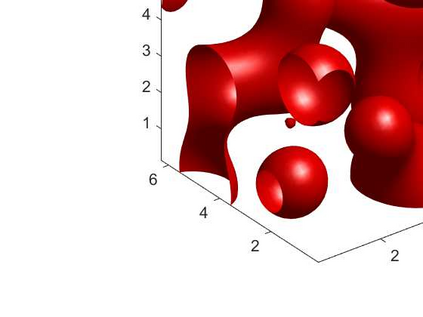
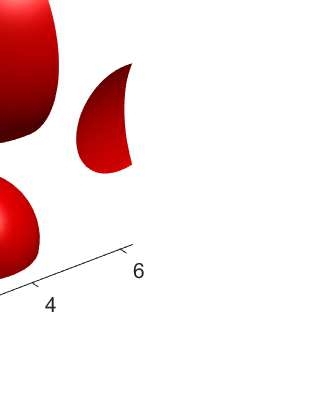
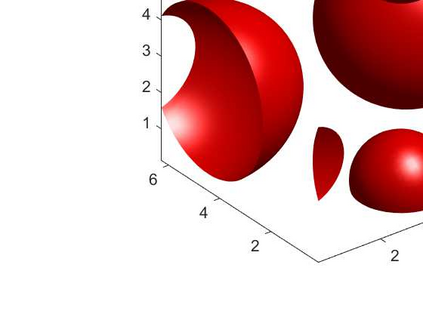
An adaptive implicit-explicit (IMEX) BDF2 scheme is investigated on generalized SAV approach for the Cahn-Hilliard equation by combining with Fourier spectral method in space. It is proved that the modified energy dissipation law is unconditionally preserved at discrete levels. Under a mild ratio restriction, i.e., \Ass{1}: $0<r_k:=\tau_k/\tau_{k-1}< r_{\max}\approx 4.8645$, we establish a rigorous error estimate in $H^1$-norm and achieve optimal second-order accuracy in time. The proof involves the tools of discrete orthogonal convolution (DOC) kernels and inequality zoom. It is worth noting that the presented adaptive time-step scheme only requires solving one linear system with constant coefficients at each time step. In our analysis, the first-consistent BDF1 for the first step does not bring the order reduction in $H^1$-norm. The $H^1$ bound of the numerical solution under periodic boundary conditions can be derived without any restriction (such as zero mean of the initial data). Finally, numerical examples are provided to verify our theoretical analysis and the algorithm efficiency.
翻译:通过与空间中的Fleier光谱法结合,对Cahn-Hilliard等式的通用SAV方法的适应性隐含(IMEX) BDF2计划进行了调查,与空间中的Fleier光谱法相结合,证明经修改的能量消散法无条件保留在离散水平上。在温和比例限制下,即Ass{1}:0<r_k: ⁇ tau_k/\\\tau ⁇ k-1 ⁇ r ⁇ max4.8645美元,我们用1美元诺尔计算出严格的误差估计数,并实现最佳的二级精确度。证据涉及离散或远端内核(DOC)和不平等缩放工具。值得指出的是,提出的适应性时间步骤方案只要求在每个步骤解决一个具有恒定系数的线性系统。在我们的分析中,第一个步骤的首列的BDFDF1不会使顺序减少1美元-诺尔姆。在定期边界条件下的数字解决方案的1美元约束下是1美元,在定期边界条件下的基质和不平等缩数分析中可以得出任何限制的模型(例如的数值分析)。