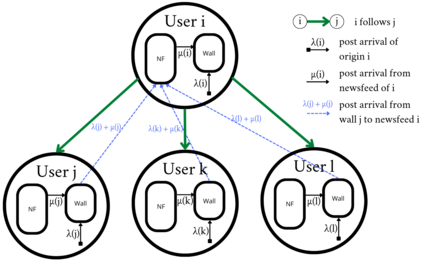
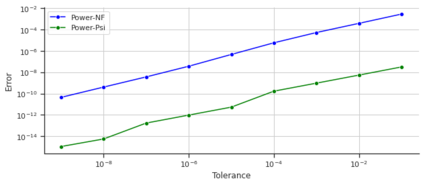
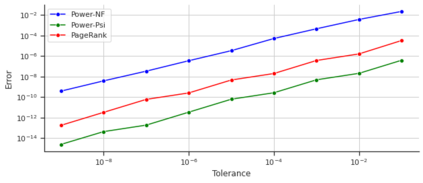
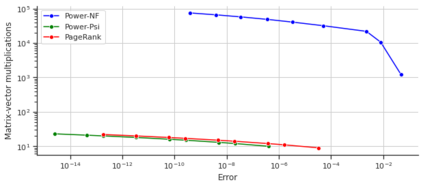
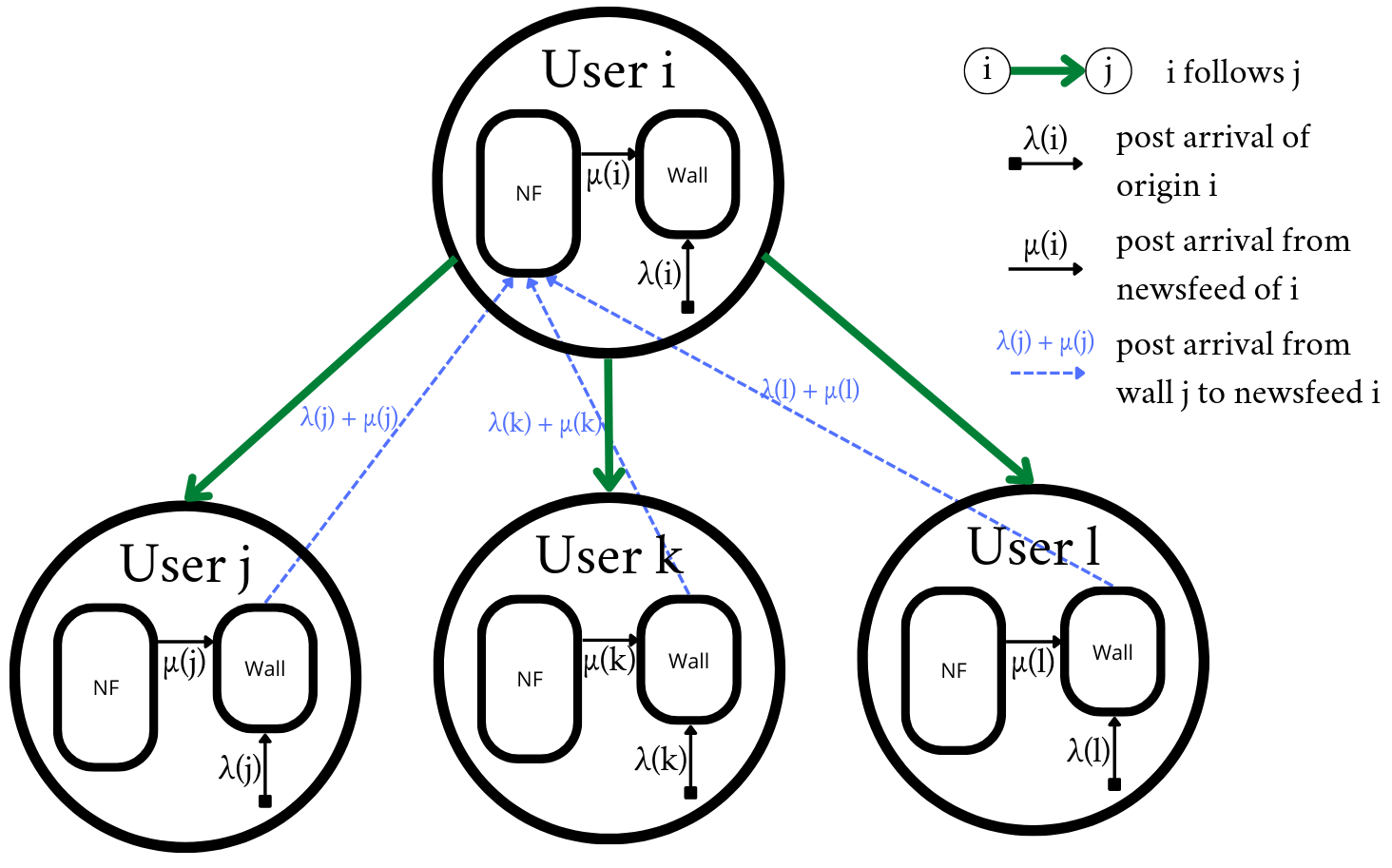
Measuring the influence of users in social networks is key for numerous applications. A recently proposed influence metric, coined as $\psi$-score, allows to go beyond traditional centrality metrics, which only assess structural graph importance, by further incorporating the rich information provided by the posting and re-posting activity of users. The $\psi$-score is shown in fact to generalize PageRank for non-homogeneous node activity. Despite its significance, it scales poorly to large datasets; for a network of $N$ users, it requires to solve $N$ linear systems of equations of size $N$. To address this problem, this work introduces a novel scalable algorithm for the fast approximation of $\psi$-score, named \textit{Power}-$\psi$. The proposed algorithm is based on a novel equation indicating that it suffices to solve one system of equations of size $N$ to compute the $\psi$-score. Then, our algorithm exploits the fact that such a system can be recursively and distributedly approximated to any desired error. This permits the $\psi$-score, summarizing both structural and behavioral information for the nodes, to run as fast as PageRank. We validate the effectiveness of the proposed algorithm, which we release as an open source Python library, on several real-world datasets.
翻译:衡量社交网络用户影响是许多应用的关键。 最近提出的影响力衡量标准(以美元计价)可以超越传统的核心度量,而传统的中心度度度指标只能评估结构图的重要性,而传统的中心度度指标只能通过进一步整合用户张贴和重新发送活动提供的丰富信息,从而进一步纳入结构图的重要性。 $/ 美元分数在事实上显示将PageRank 概括为非同质节点活动。 尽管它的意义重大,但它比大数据集规模要小; 对于一个由美元组成的用户网络,它需要解决规模为$N的等式线性系统。 为了解决这个问题,这项工作引入了一种新型的可缩放算法,用于快速接近$/psi-count-scountal, 命名为\ textitilit{power}- $/ presidiocial $。提议的算法基于一种新方程的公式,表明它足以解决一个规模为$N美元的方程系统,以计算成大的数据集。然后,我们的算法利用这样一种事实,即这样一个系统可以循环地和分布式的系统,可以作为我们所期望中的一种结构的算法, 的排序, 用于快速校正判算。