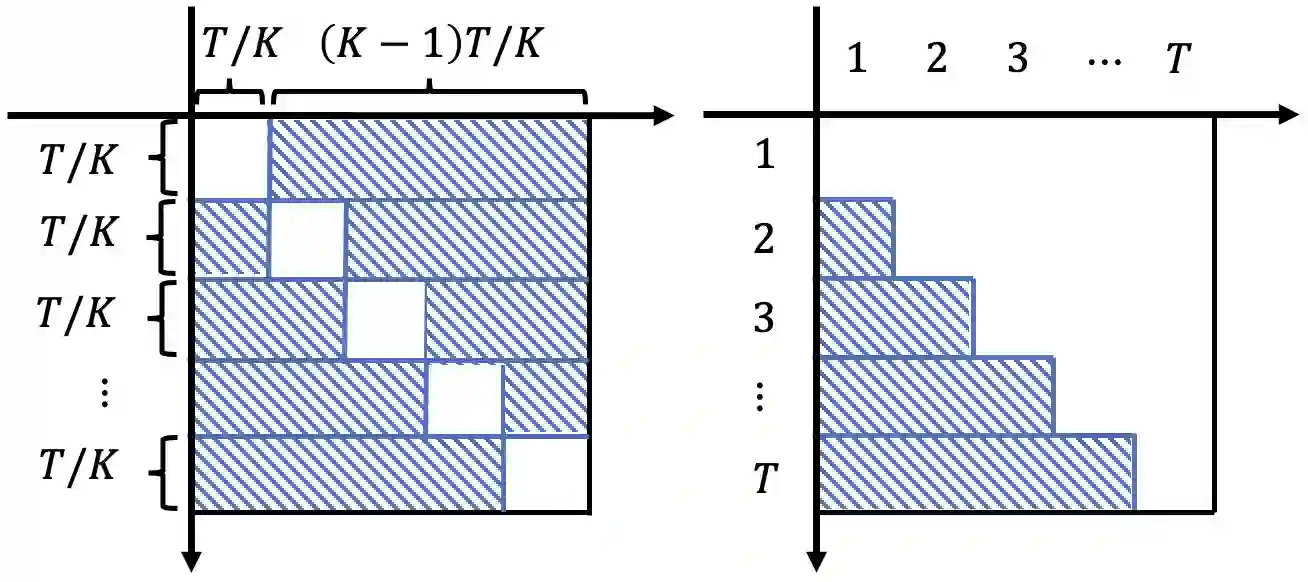
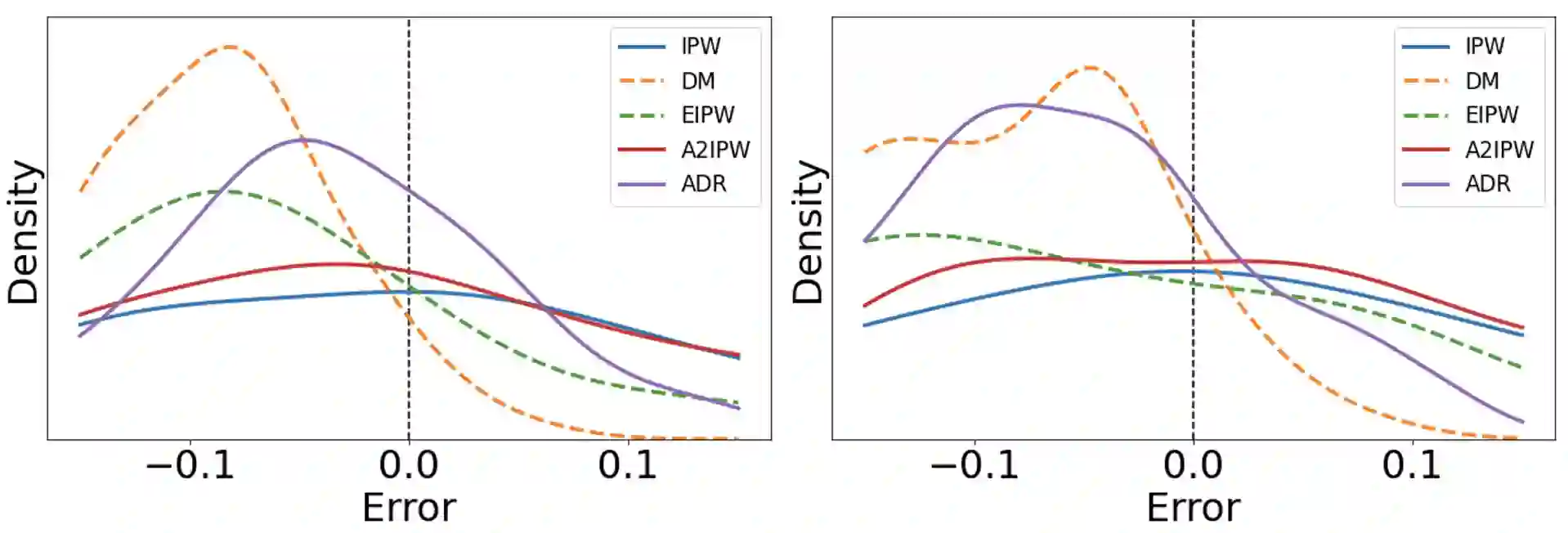
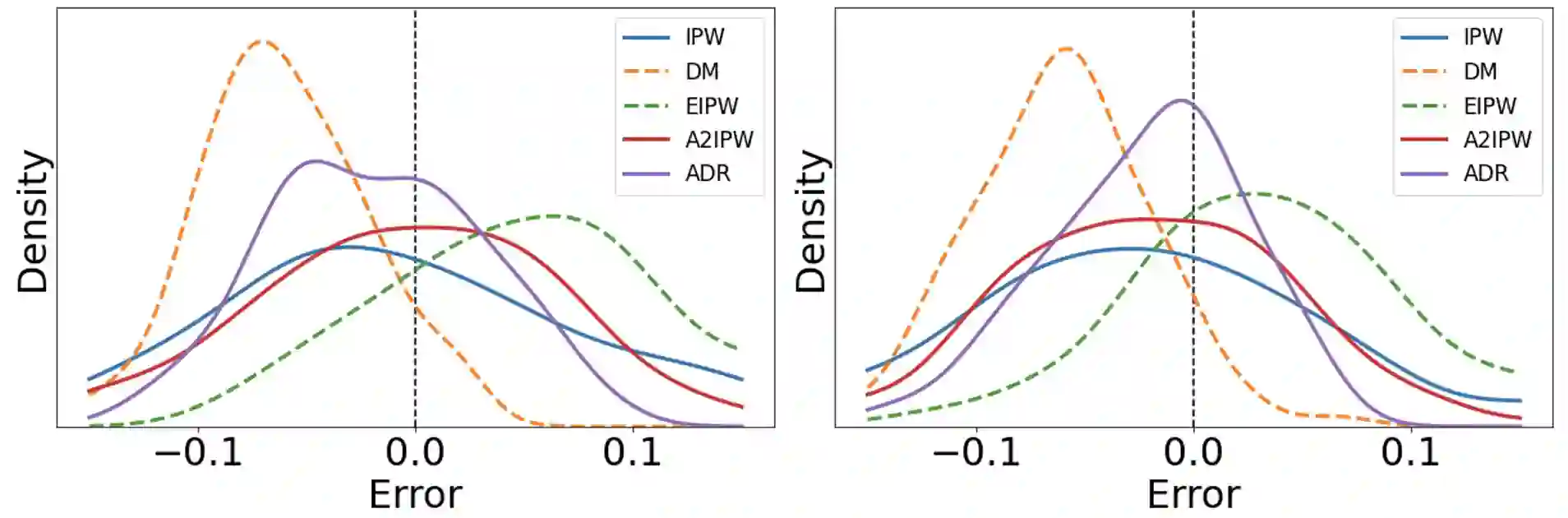
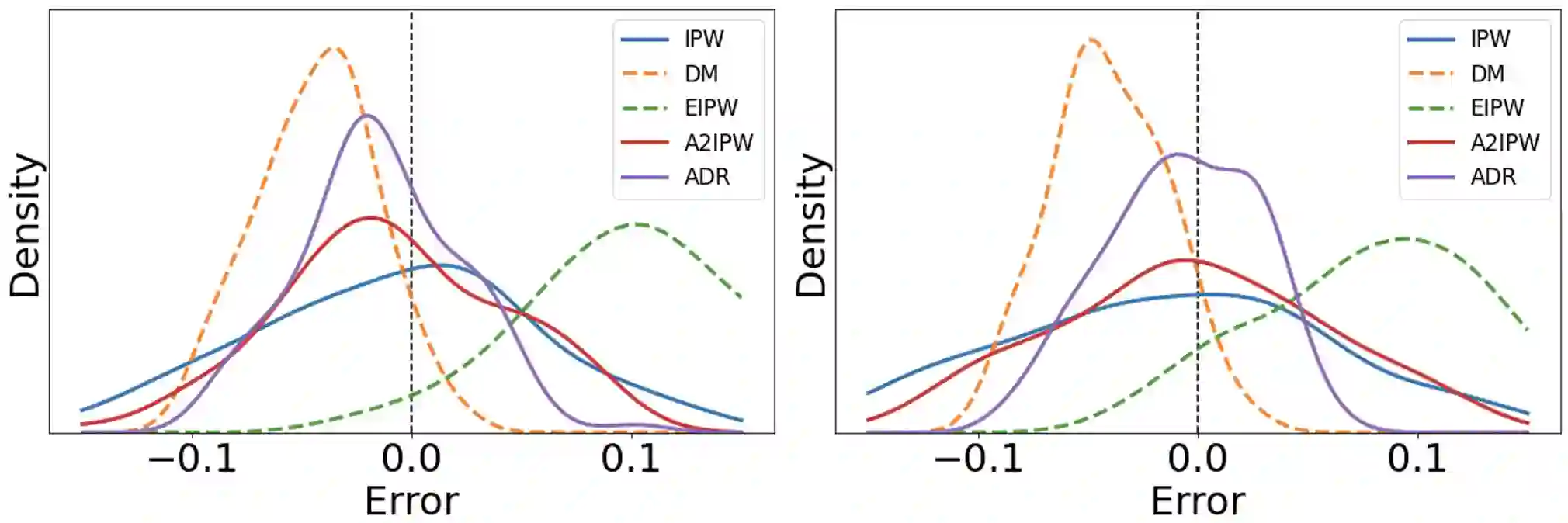
A doubly robust (DR) estimator is crucial in causal inference, which consists of two nuisance parameters: the conditional mean outcome and logging policy (probability of choosing an action). This paper provides a DR estimator for dependent samples obtained in adaptive experiments and introduces two related topics. First, we propose adaptive-fitting as a variant of sample-splitting for showing an asymptotically normal semiparametric estimator from dependent samples without non-Donsker nuisance estimators. Second, we report an empirical paradox that a DR estimator shows better performances than other estimators using the true logging policy instead of its estimator. While a similar phenomenon is also known for estimators with i.i.d. samples, we hypothesize that traditional explanations based on asymptotic efficiency cannot elucidate our case with dependent samples. We confirm this hypothesis through simulation studies.
翻译:双重强力估计(DR)在因果推断中至关重要,它包括两个骚扰性参数:有条件平均结果和伐木政策(选择行动的可能性),本文为在适应性实验中获得的依附样品提供了一个DR估计值,并介绍了两个相关专题。首先,我们提议将适应性调整作为样本分割的变体,以显示一个无症状正常的半参数估计值,而没有非唐斯克骚扰性估计值。第二,我们报告一个经验悖论,即DR估计值比使用真实伐木政策而不是其估计值的其他估计值显示更好的性能。虽然使用i.i.d.样本的估测者也知道类似的现象,但我们对基于无症状效率的传统解释不能用依赖性样品来解释我们的情况进行了假设。我们通过模拟研究来证实这一假设。