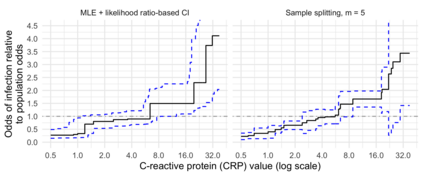
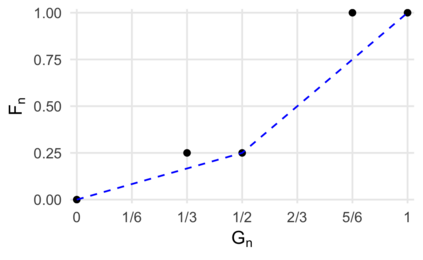
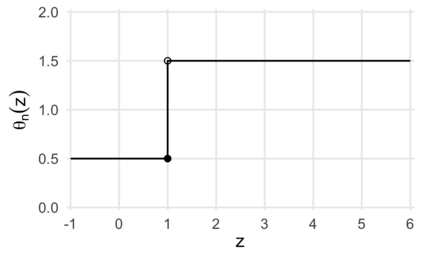
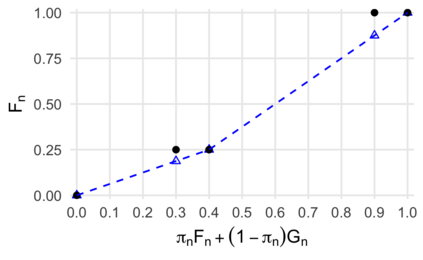
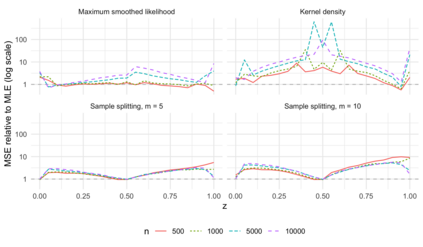
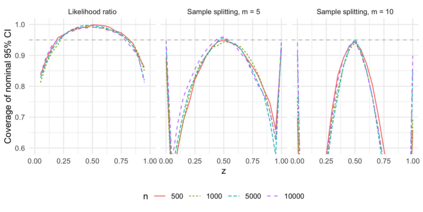
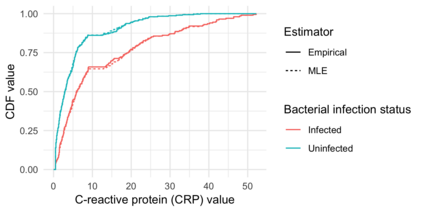
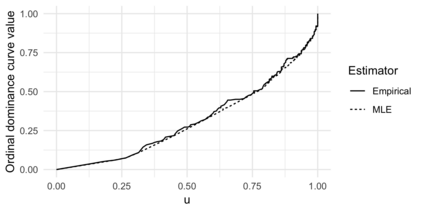
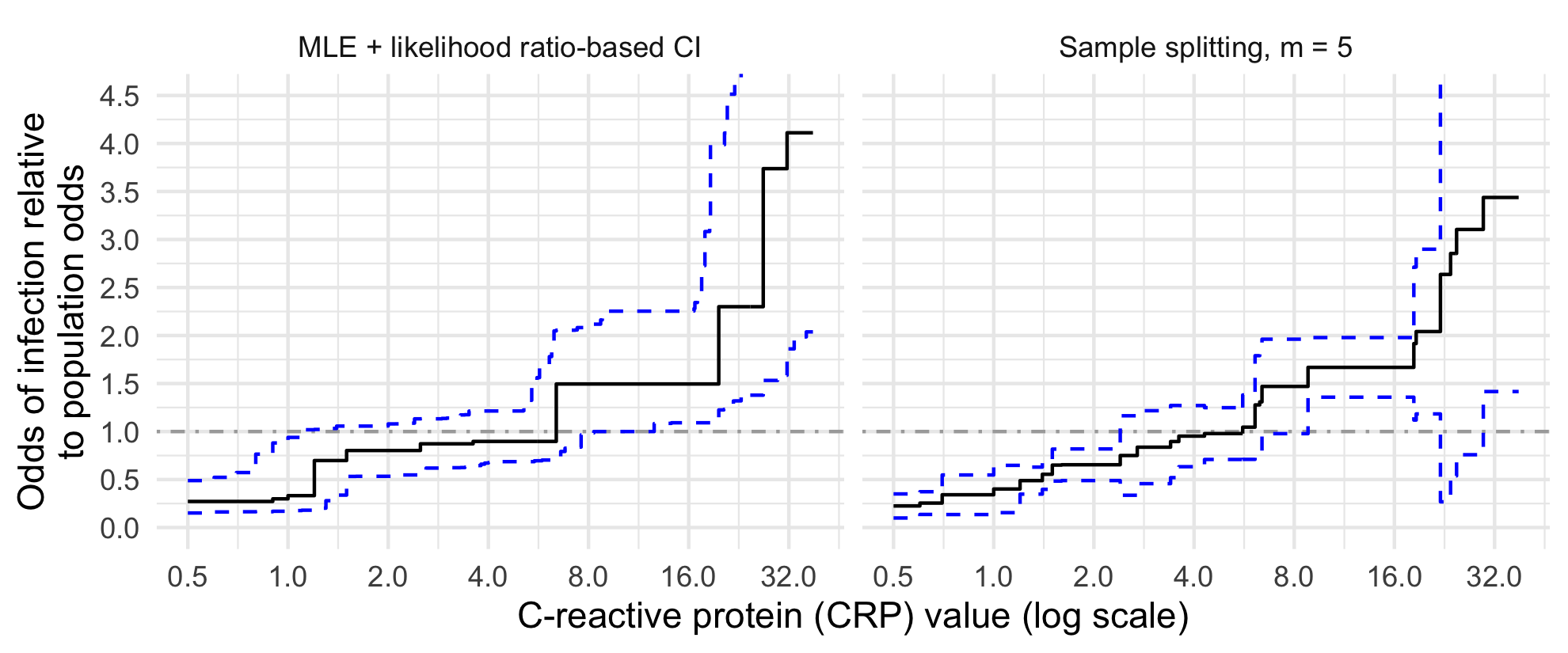
Comparison of two univariate distributions based on independent samples from them is a fundamental problem in statistics, with applications in a wide variety of scientific disciplines. In many situations, we might hypothesize that the two distributions are stochastically ordered, meaning intuitively that samples from one distribution tend to be larger than those from the other. One type of stochastic order that arises in economics, biomedicine, and elsewhere is the likelihood ratio order, also known as the density ratio order, in which the ratio of the density functions of the two distributions is monotone non-decreasing. In this article, we derive and study the nonparametric maximum likelihood estimator of the individual distributions and the ratio of their densities under the likelihood ratio order. Our work applies to discrete distributions, continuous distributions, and mixed continuous-discrete distributions. We demonstrate convergence in distribution of the estimator in certain cases, and we illustrate our results using numerical experiments and an analysis of a biomarker for predicting bacterial infection in children with systemic inflammatory response syndrome.
翻译:比较基于独立样本的两种单象体分布,这是统计中的一个基本问题,在多种科学学科的应用中,这都是一个根本性的问题。在许多情况下,我们可以假设这两种分布是随机排列的,直观地说,一种分布的样本往往大于另一种分布的样本。一种在经济学、生物医学和其他地方产生的随机排列顺序是概率比顺序,也称为密度比率顺序,两种分布的密度函数比是单体酮不降解的。在本篇文章中,我们得出并研究个别分布的不可比较的最大概率估计器及其密度在概率比率顺序下的比例。我们的工作适用于分体分布、连续分布和混合连续分泌分布。我们在某些案例中显示了估计器分布的趋同,我们用数字实验和分析生物标记仪来预测儿童在系统炎综合症下的细菌感染情况。我们的工作适用于分散分布、连续分布和混合连续分解分布。我们在某些案例中显示了估计器的分布的趋同,我们用数字实验和生物标记仪来说明我们的结果。