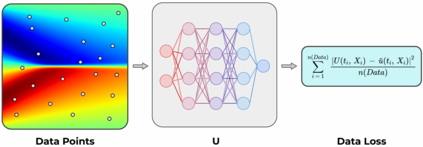
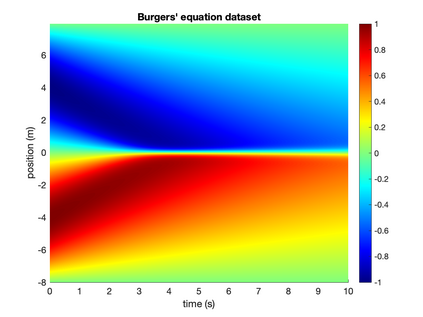
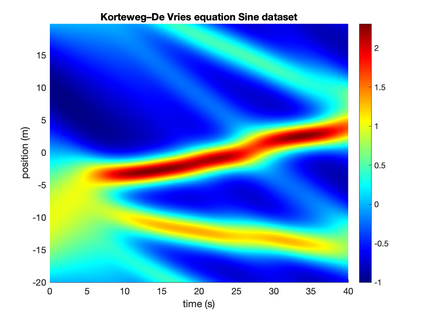
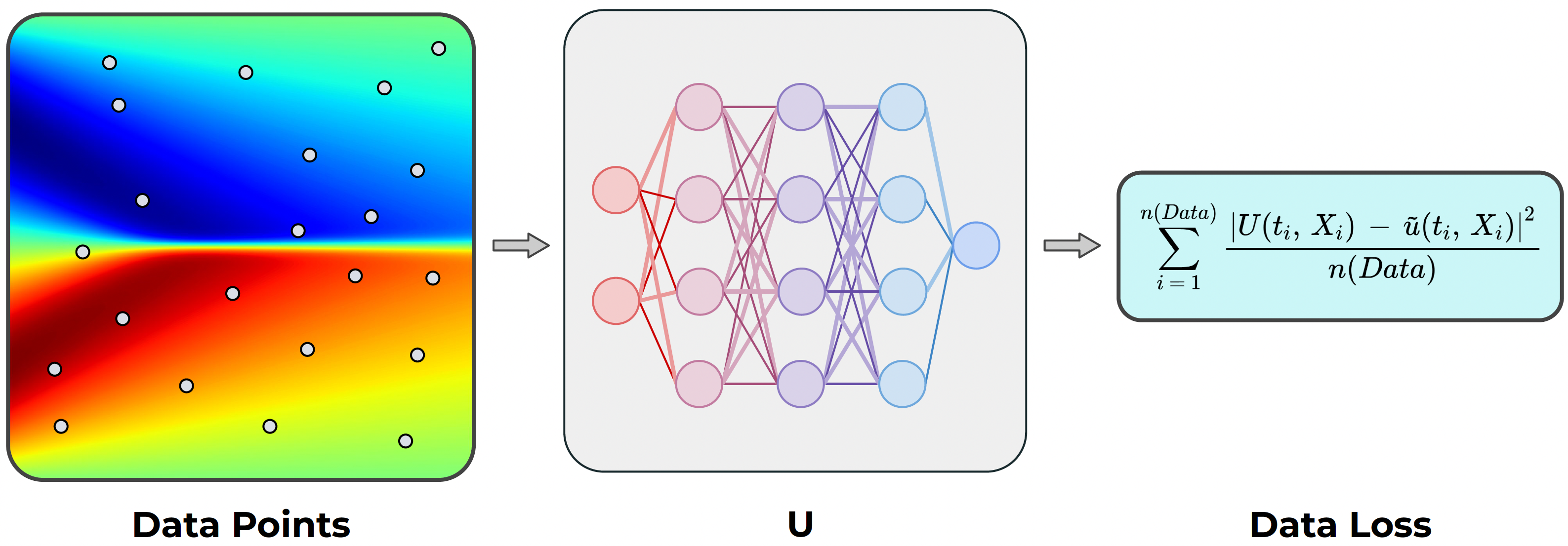
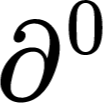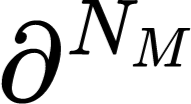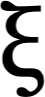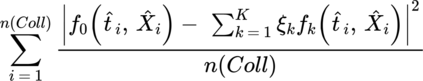In this paper, we introduce PDE-LEARN, a novel PDE discovery algorithm that can identify governing partial differential equations (PDEs) directly from noisy, limited measurements of a physical system of interest. PDE-LEARN uses a Rational Neural Network, $U$, to approximate the system response function and a sparse, trainable vector, $\xi$, to characterize the hidden PDE that the system response function satisfies. Our approach couples the training of $U$ and $\xi$ using a loss function that (1) makes $U$ approximate the system response function, (2) encapsulates the fact that $U$ satisfies a hidden PDE that $\xi$ characterizes, and (3) promotes sparsity in $\xi$ using ideas from iteratively reweighted least-squares. Further, PDE-LEARN can simultaneously learn from several data sets, allowing it to incorporate results from multiple experiments. This approach yields a robust algorithm to discover PDEs directly from realistic scientific data. We demonstrate the efficacy of PDE-LEARN by identifying several PDEs from noisy and limited measurements.
翻译:在本文中,我们引入了PDE-LEARN(PDE-LEARN),这是一种新型的PDE-LEARN(PDE-LEARN)发现算法,它能够直接从噪音中确定部分差异方程式(PDE-PDE-LEARs),对一个感兴趣的物理系统进行有限的测量。PDE-LEARN使用一个合理神经网络($U美元)来估计系统反应功能,并使用一个分散的、可培训的矢量器($xI美元)来估计系统反应功能所满足的隐藏方程式(PDE-PDEs) 。PDE-LEARN(PDE-LEARN)可以同时从多个数据集中学习,从而将多个实验的结果纳入其中。我们的方法产生了一种强大的算法,可以直接从现实的科学数据中发现PDE-LEARN(PDE-LEARN)的功效,我们通过确定几个来自噪音和有限的测量的PDES(PDEs)。