Stability Analysis of Fractional Order Memristor Synapse-coupled Hopfield Neural Network with Ring Structure

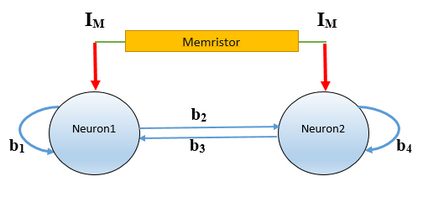
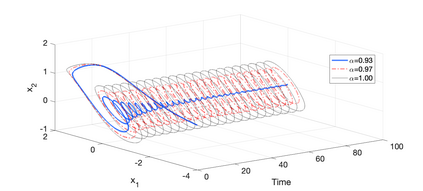
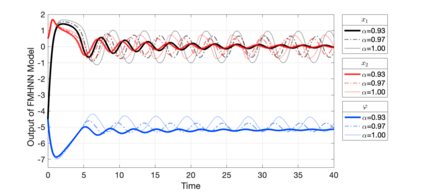
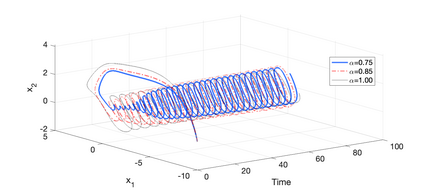
A memristor is a nonlinear two-terminal electrical element that incorporates memory features and nanoscale properties, enabling us to design very high-density artificial neural networks. To enhance the memory property, we should use mathematical frameworks like fractional calculus, which is capable of doing so. Here, we first present a fractional-order memristor synapse-coupling Hopfield neural network on two neurons and then extend the model to a neural network with a ring structure that consists of n sub-network neurons, increasing the synchronization in the network. Necessary and sufficient conditions for the stability of equilibrium points are investigated, highlighting the dependency of the stability on the fractional-order value and the number of neurons. Numerical simulations and bifurcation analysis, along with Lyapunov exponents, are given in the two-neuron case that substantiates the theoretical findings, suggesting possible routes towards chaos when the fractional order of the system increases. In the n-neuron case also, it is revealed that the stability depends on the structure and number of sub-networks.