A regularization-patching dual quaternion optimization method for solving the hand-eye calibration problem

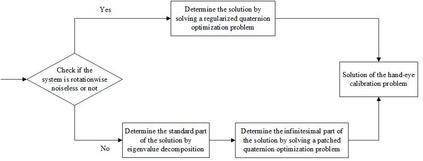
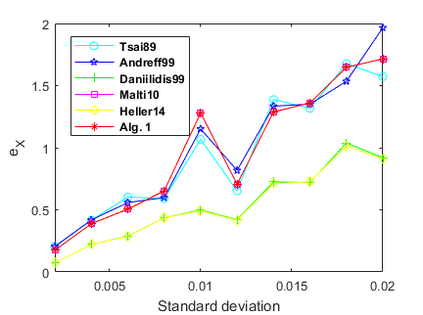
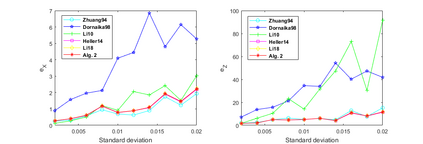
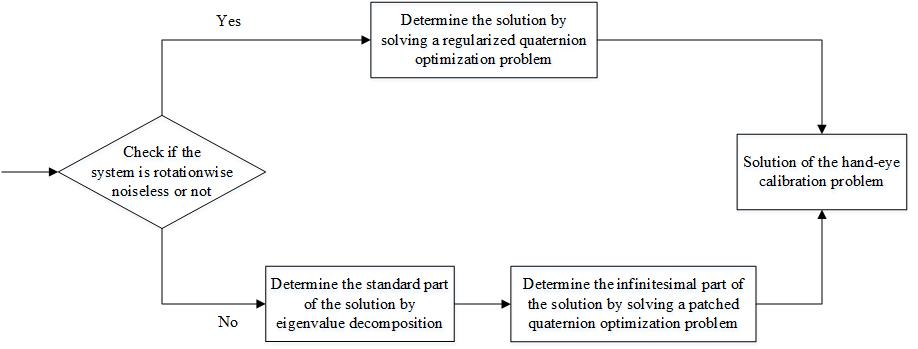
The hand-eye calibration problem is an important application problem in robot research. Based on the 2-norm of dual quaternion vectors, we propose a new dual quaternion optimization method for the hand-eye calibration problem. The dual quaternion optimization problem is decomposed to two quaternion optimization subproblems. The first quaternion optimization subproblem governs the rotation of the robot hand. It can be solved efficiently by the eigenvalue decomposition or singular value decomposition. If the optimal value of the first quaternion optimization subproblem is zero, then the system is rotationwise noiseless, i.e., there exists a ``perfect'' robot hand motion which meets all the testing poses rotationwise exactly. In this case, we apply the regularization technique for solving the second subproblem to minimize the distance of the translation. Otherwise we apply the patching technique to solve the second quaternion optimization subproblem. Then solving the second quaternion optimization subproblem turns out to be solving a quadratically constrained quadratic program. In this way, we give a complete description for the solution set of hand-eye calibration problems. This is new in the hand-eye calibration literature. The numerical results are also presented to show the efficiency of the proposed method.