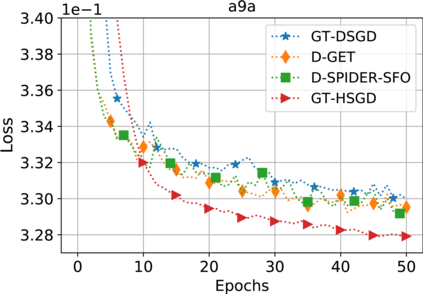
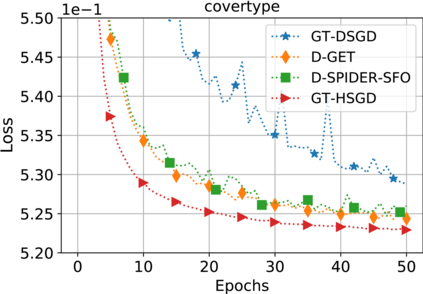
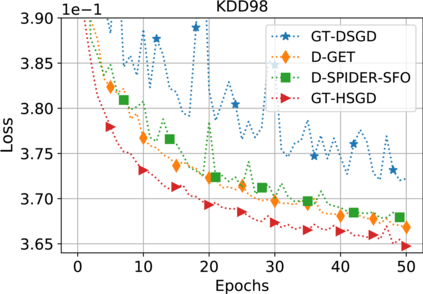
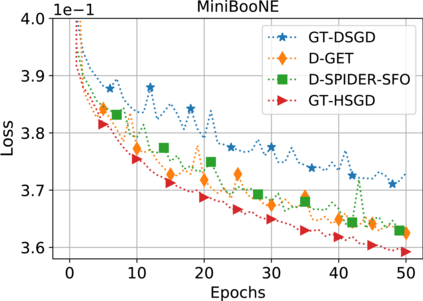
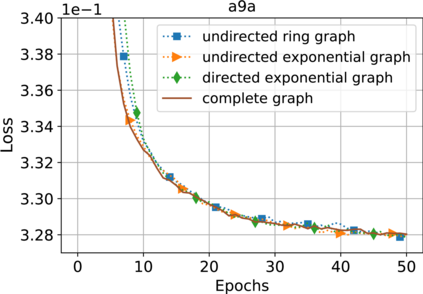
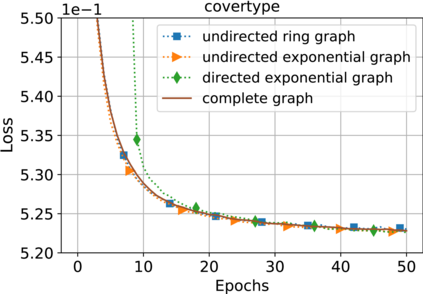
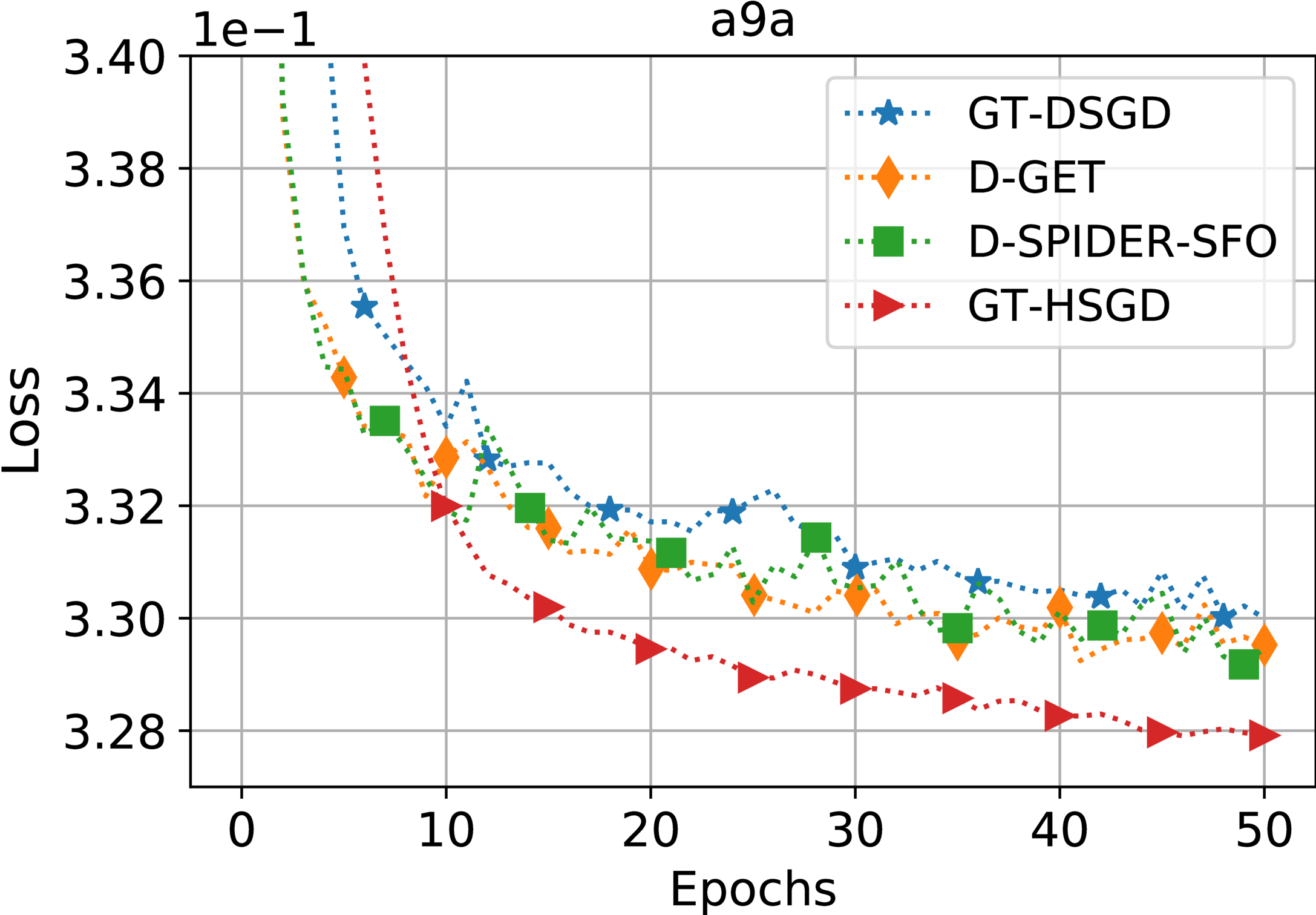
This paper considers decentralized stochastic optimization over a network of $n$ nodes, where each node possesses a smooth non-convex local cost function and the goal of the networked nodes is to find an $\epsilon$-accurate first-order stationary point of the sum of the local costs. We focus on an online setting, where each node accesses its local cost only by means of a stochastic first-order oracle that returns a noisy version of the exact gradient. In this context, we propose a novel single-loop decentralized hybrid variance-reduced stochastic gradient method, called GT-HSGD, that outperforms the existing approaches in terms of both the oracle complexity and practical implementation. The GT-HSGD algorithm implements specialized local hybrid stochastic gradient estimators that are fused over the network to track the global gradient. Remarkably, GT-HSGD achieves a network topology-independent oracle complexity of $O(n^{-1}\epsilon^{-3})$ when the required error tolerance $\epsilon$ is small enough, leading to a linear speedup with respect to the centralized optimal online variance-reduced approaches that operate on a single node. Numerical experiments are provided to illustrate our main technical results.
翻译:本文考虑对一个由美元节点组成的网络进行分散式随机优化,每个节点拥有一个平滑的非混凝土本地成本功能,而网络节点的目标是找到一个单位成本和当地成本之和的一阶固定点。我们关注一个在线设置,每个节点只能通过一个随机第一阶或触角进入其本地成本,从而返回精确梯度的响亮版本。在这方面,我们提议一种新型的单一环分散式混合差异降压梯度方法,称为GT-HSGD,该方法在质谱复杂性和实际实施方面优于现有方法。GT-HSGD算法采用了专门的本地混合性梯度估计器,该方法与网络连接,以跟踪全球梯度。值得注意的是,当所需的错误容忍美元-Central-plock-lockencation 3 方法($N°=1 ⁇ -1 ⁇ -epslon}在网络上具有依赖性结构复杂性的复杂度时,当要求的错误容忍度($\/eplon=3美元)超过现有方法时, 以最优度进行最佳的线性实验时,该方法在网络上没有多少。