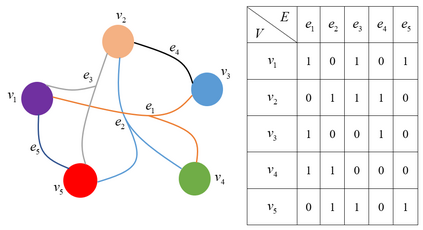
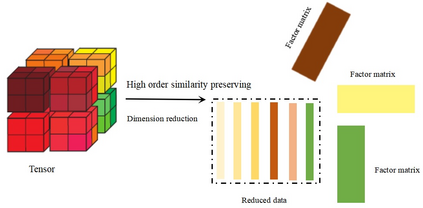
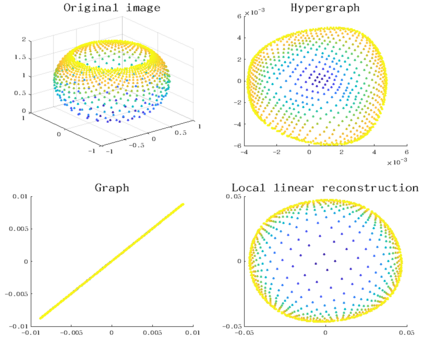
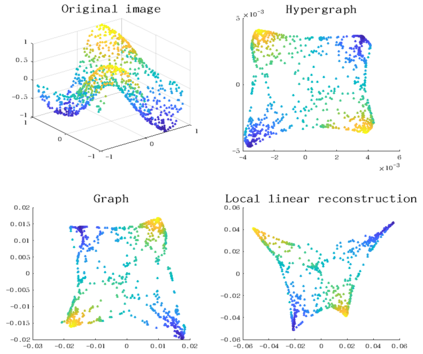
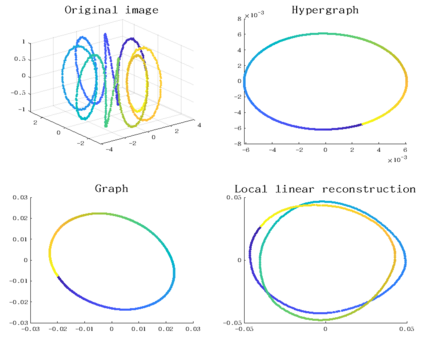
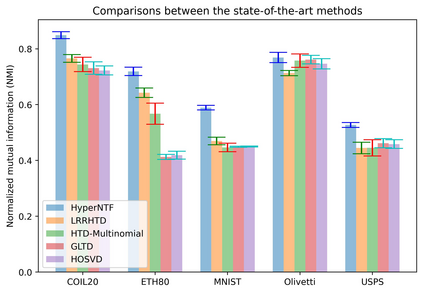
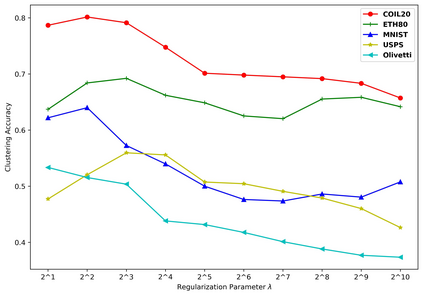
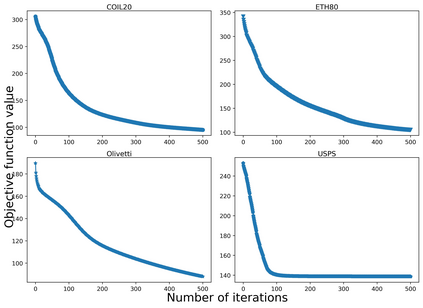
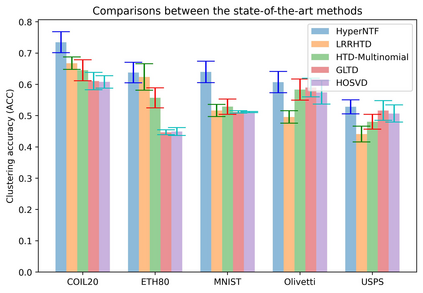
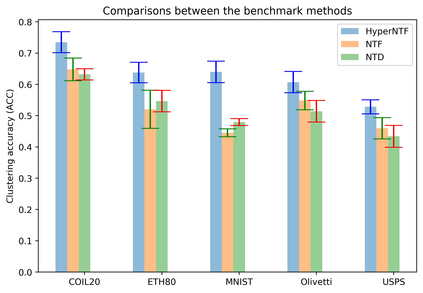
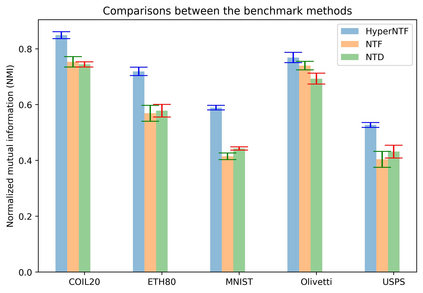
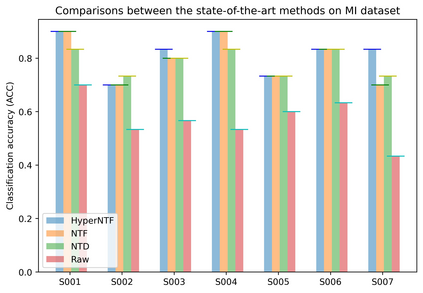
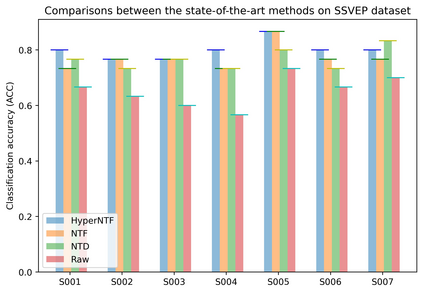
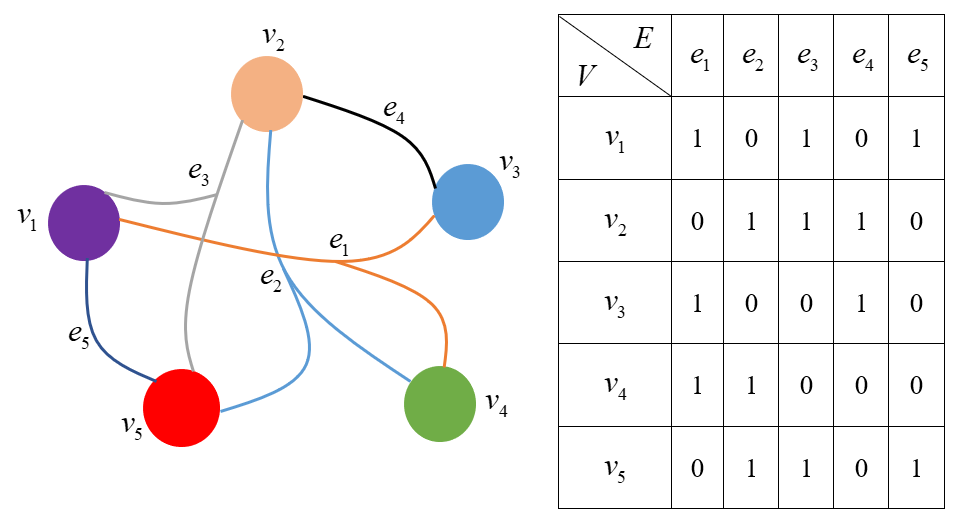
Tensor decomposition is an effective tool for learning multi-way structures and heterogeneous features from high-dimensional data, such as the multi-view images and multichannel electroencephalography (EEG) signals, are often represented by tensors. However, most of tensor decomposition methods are the linear feature extraction techniques, which are unable to reveal the nonlinear structure within high-dimensional data. To address such problem, a lot of algorithms have been proposed for simultaneously performs linear and non-linear feature extraction. A representative algorithm is the Graph Regularized Non-negative Matrix Factorization (GNMF) for image clustering. However, the normal 2-order graph can only models the pairwise similarity of objects, which cannot sufficiently exploit the complex structures of samples. Thus, we propose a novel method, named Hypergraph Regularized Non-negative Tensor Factorization (HyperNTF), which utilizes hypergraph to encode the complex connections among samples and employs the factor matrix corresponding with last mode of Canonical Polyadic (CP) decomposition as low-dimensional representation. Extensive experiments on synthetic manifolds, real-world image datasets, and EEG signals, demonstrating that HyperNTF outperforms the state-of-the-art methods in terms of dimensionality reduction, clustering, and classification.
翻译:电离分解是学习多路结构以及高维数据(如多视图像和多通道电子脑光学信号)的不同特征的有效工具,例如多视图像和多通道电子感光学信号,这些信号往往由数以数方表示,然而,大多数高温分解方法都是线性地貌提取技术,无法在高维数据中揭示非线性结构。为解决这一问题,已提出大量算法,用于同时进行线性和非线性特征提取。一种代表性算法是用于图像群集的定型非负矩阵质化(GNMF)图。然而,正常的2级图只能模拟对相近性,无法充分利用复杂的样品结构。因此,我们提出了一个新颖的方法,即名为超光学非线性非线性电离线性电离子集集成法(HyperNTF),该方法利用超光谱法对样本之间的复杂连接进行编码,并使用与Cenical Poldic(CP)最后一种模式相对的因子矩阵分解分解矩阵,作为低维代表。正常的对等的物体的图,而只能模拟图图只能模拟图只能模拟模拟模拟模拟模拟模拟模拟模拟模拟模拟模拟模拟,在合成的对称中进行广泛的实验,在合成的模型中演示,在合成的合成的合成、真实性、超载式的合成的图像流式的图像流学-级模型中演示。