Robust Perron Cluster Analysis for coarse-graining of non-reversible stochastic matrices with complex eigenvalues

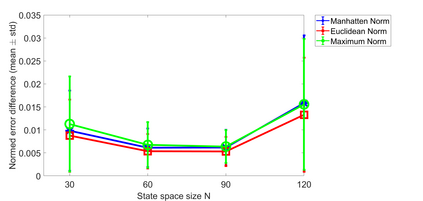
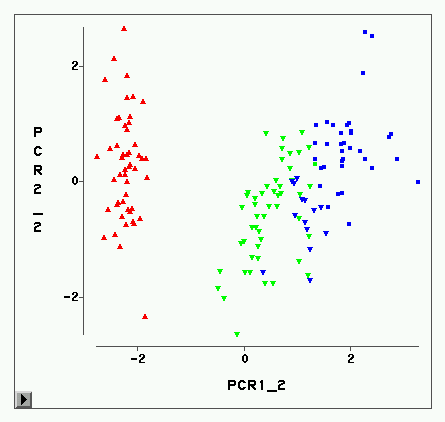
The Robust Perron Cluster Analysis (PCCA+) has become a popular algorithm for coarse-graining transition matrices of nearly decomposable Markov chains with transition states. Though originally developed for reversible Markov chains, it has been shown previously that PCCA+ can also be applied to cluster non-reversible Markov chains. However, the algorithm was implemented by assuming the dominant (target) eigenvalues to be real numbers. Therefore, the generalized Robust Perron Cluster Analysis (G-PCCA+) has recently been developed. G-PCCA+ is based on real Schur vectors instead of eigenvectors and can therefore be used to also coarse-grain transition matrices with complex eigenvalues. In its current implementation, however, G-PCCA+ is computationally expensive, which limits its applicability to large matrix problems. In this paper, we demonstrate that PCCA+ works in fact on any dominant invariant subspace of a nearly decomposable transition matrix, including both Schur vectors and eigenvectors. In particular, by separating the real and imaginary parts of complex eigenvectors, PCCA+ also works for transition matrices that have complex eigenvalues, including matrices with a circular transition pattern. We show that this separation maintains the invariant subspace, and that our version of the PCCA+ algorithm results in the same coarse-grained transition matrices as G-PCCA+, whereby PCCA+ is consistently faster in runtime than G-PCCA+. The analysis is performed in the Matlab programming language and codes are provided.