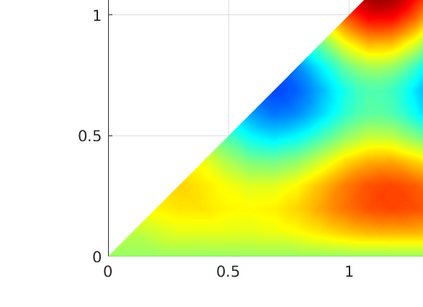
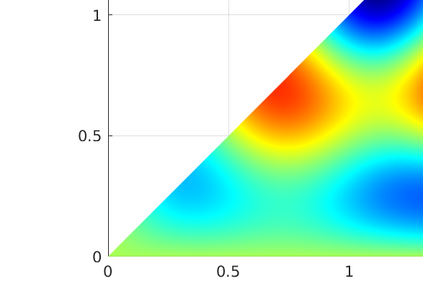
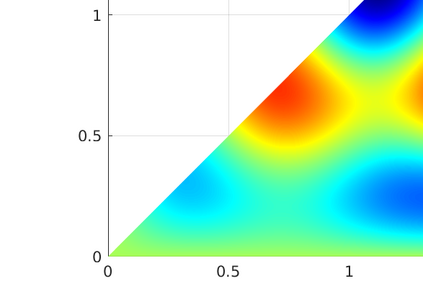
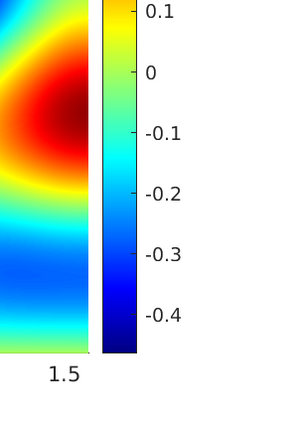
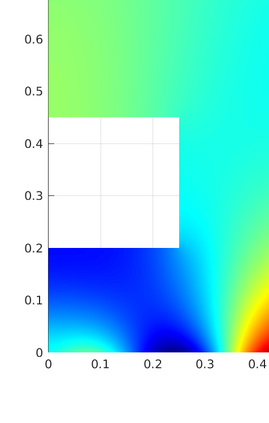
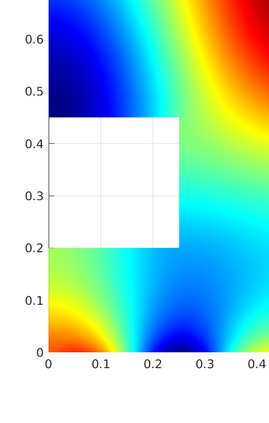
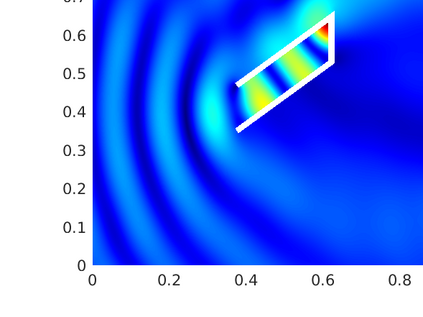
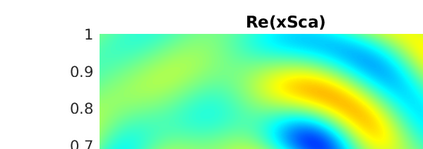
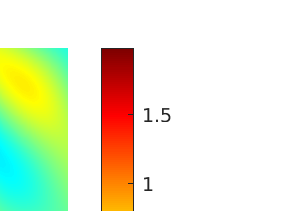
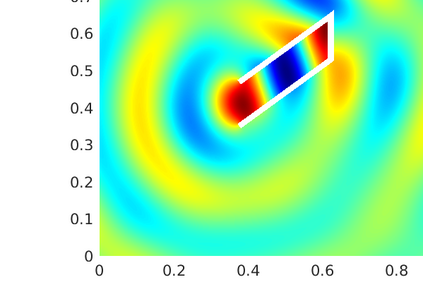
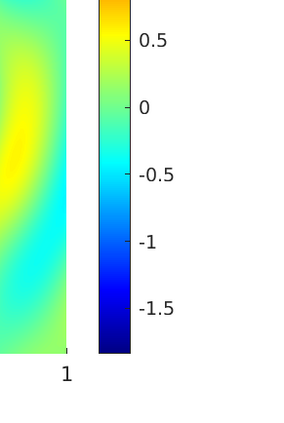
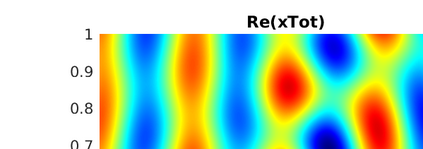
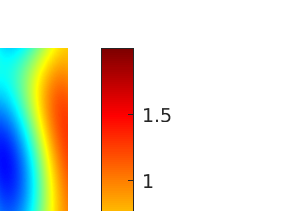
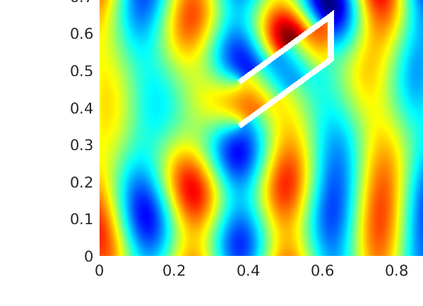
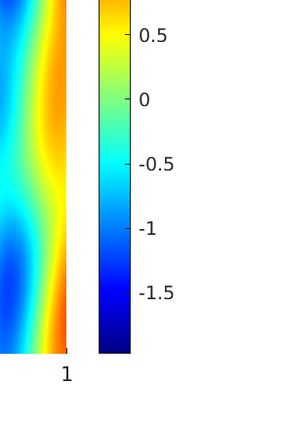
We introduce several spatially adaptive model order reduction approaches tailored to non-coercive elliptic boundary value problems, specifically, parametric-in-frequency Helmholtz problems. The offline information is computed by means of adaptive finite elements, so that each snapshot lives in a different discrete space that resolves the local singularities of the analytical solution and is adjusted to the considered frequency value. A rational surrogate is then assembled adopting either a least-squares or an interpolatory approach, yielding function-valued version of the standard rational interpolation method ($\mathcal{V}$-SRI) and the minimal rational interpolation method (MRI). In the context of building an approximation for linear or quadratic functionals of the Helmholtz solution, we perform several numerical experiments to compare the proposed methodologies. Our simulations show that, for interior resonant problems (whose singularities are encoded by poles on the real axis), the spatially adaptive $\mathcal{V}$-SRI and MRI work comparably well. Instead, when dealing with exterior scattering problems, whose frequency response is mostly smooth, the $\mathcal{V}$-SRI method seems to be the best-performing one.
翻译:我们引入了几种空间适应性模式序列减少模型,这些模型是针对非胁迫性的椭圆边界值问题,具体来说,是赫尔莫霍尔茨频中参数值问题。离线信息是用适应性有限元素来计算的,这样每张快照都生活在不同的离散空间中,可以解决分析解决方案的本地独特性,并调整到考虑的频率值。一个合理的代谢器随后组合采用最小方或内插法,产生标准合理间推法(mathcal{V}$-SRI)和最低合理间推法(MRI)的功能价值价值值版本。在为赫尔莫赫茨解决方案的线性或四边函数建立近似值的背景下,我们进行了数项数字实验,以比较拟议的方法。我们的模拟显示,对于内部共振荡问题(其独有实际轴上的极值),空间适应性合理调整 $\math cal{V}和MRI工作(MRI)的功能值值值不同。在与最平稳的外部问题处理时,其频率似乎是最佳的方法。