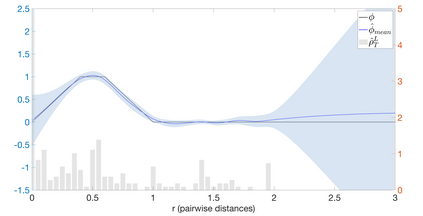
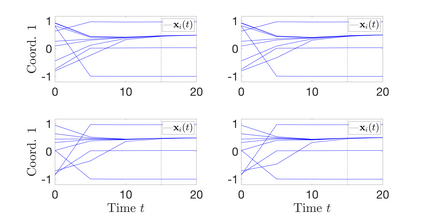
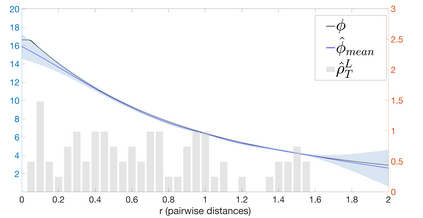
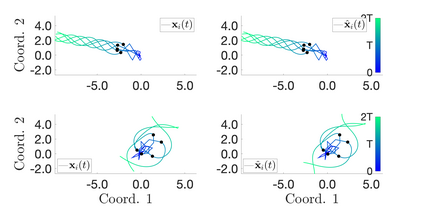
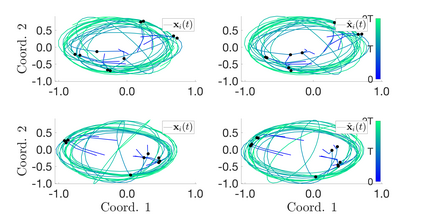
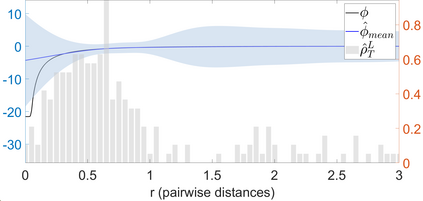
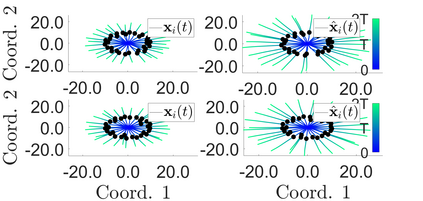
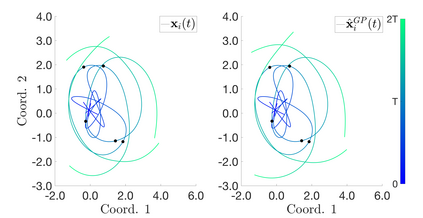
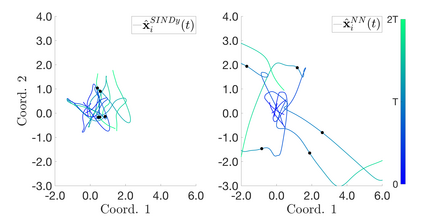
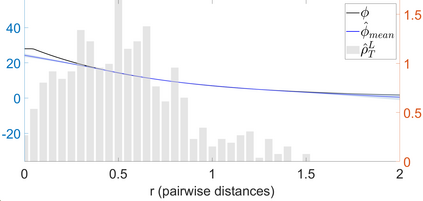
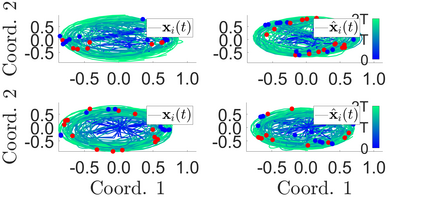
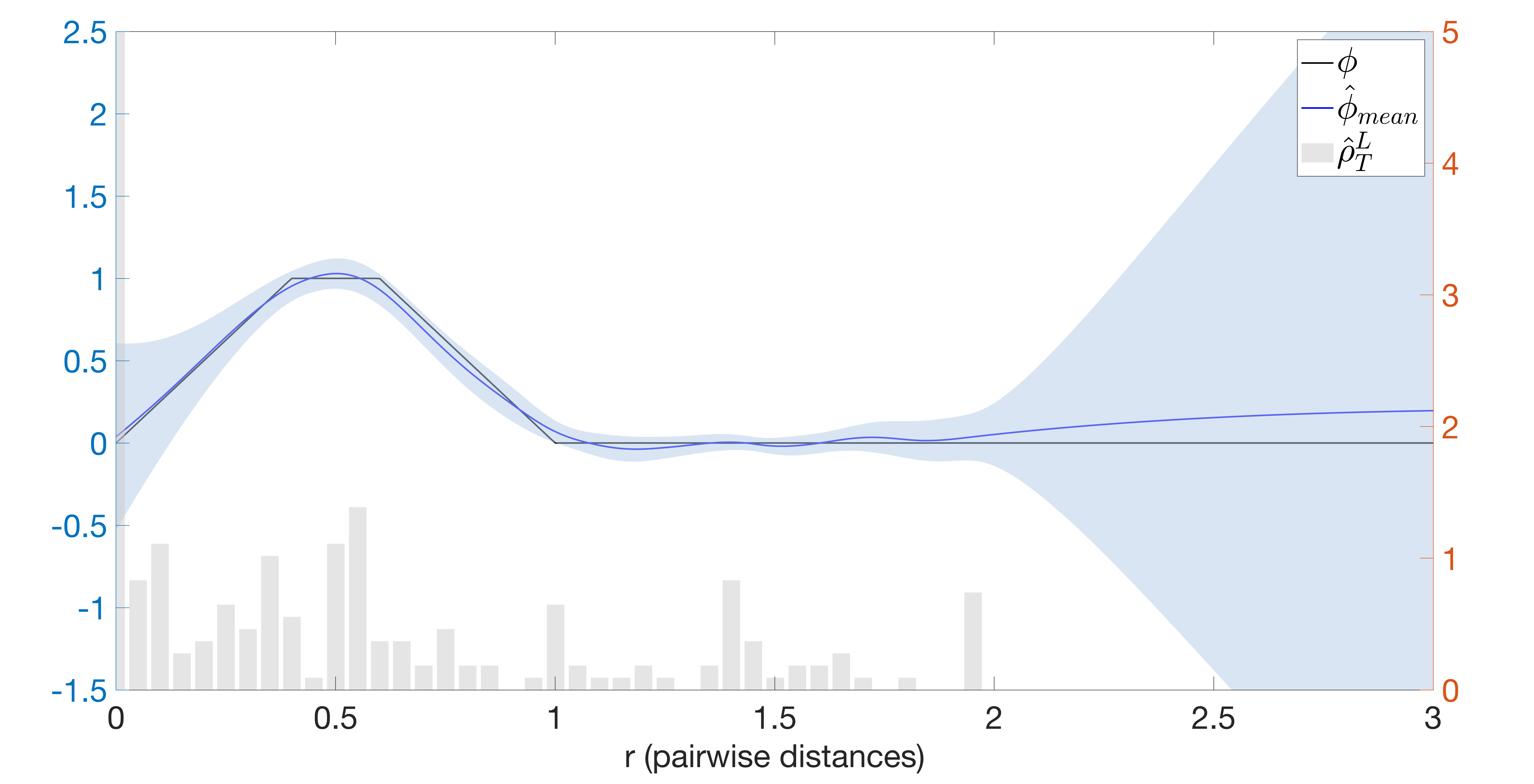
Interacting particle or agent systems that display a rich variety of swarming behaviours are ubiquitous in science and engineering. A fundamental and challenging goal is to understand the link between individual interaction rules and swarming. In this paper, we study the data-driven discovery of a second-order particle swarming model that describes the evolution of $N$ particles in $\mathbb{R}^d$ under radial interactions. We propose a learning approach that models the latent radial interaction function as Gaussian processes, which can simultaneously fulfill two inference goals: one is the nonparametric inference of {the} interaction function with pointwise uncertainty quantification, and the other one is the inference of unknown scalar parameters in the non-collective friction forces of the system. We formulate the learning problem as a statistical inverse problem and provide a detailed analysis of recoverability conditions, establishing that a coercivity condition is sufficient for recoverability. Given data collected from $M$ i.i.d trajectories with independent Gaussian observational noise, we provide a finite-sample analysis, showing that our posterior mean estimator converges in a Reproducing kernel Hilbert space norm, at an optimal rate in $M$ equal to the one in the classical 1-dimensional Kernel Ridge regression. As a byproduct, we show we can obtain a parametric learning rate in $M$ for the posterior marginal variance using $L^{\infty}$ norm, and the rate could also involve $N$ and $L$ (the number of observation time instances for each trajectory), depending on the condition number of the inverse problem. Numerical results on systems that exhibit different swarming behaviors demonstrate efficient learning of our approach from scarce noisy trajectory data.
翻译:显示大量升温行为的互换粒子或代理系统在科学和工程方面无处不在。 一个根本性和具有挑战性的目标就是理解个人互动规则与升温之间的联系。 在本文中, 我们研究数据驱动发现第二阶粒升温模型, 该模型描述美元=mathbb{R ⁇ d$的粒子在辐射互动下的演化。 我们提出一种学习方法, 将潜伏的辐射互动功能作为高斯进程模型, 它可以同时实现两个推论目标: 一个是 {the} 互动功能与点向不确定性观测的非参数推断。 另一个是 由数据驱动的第二阶梯级粒子升升模型, 该模型描述美元=美元=xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx