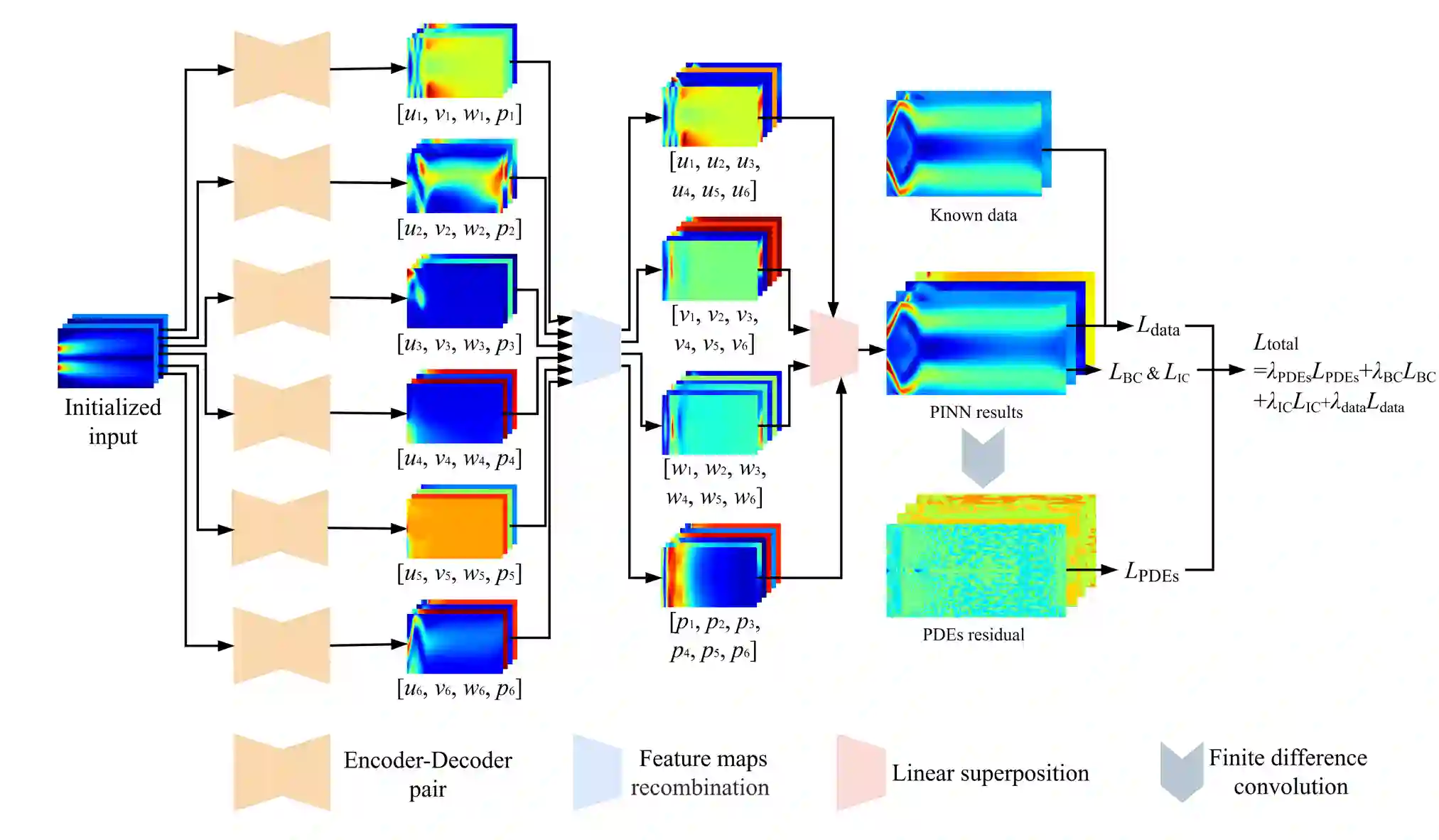
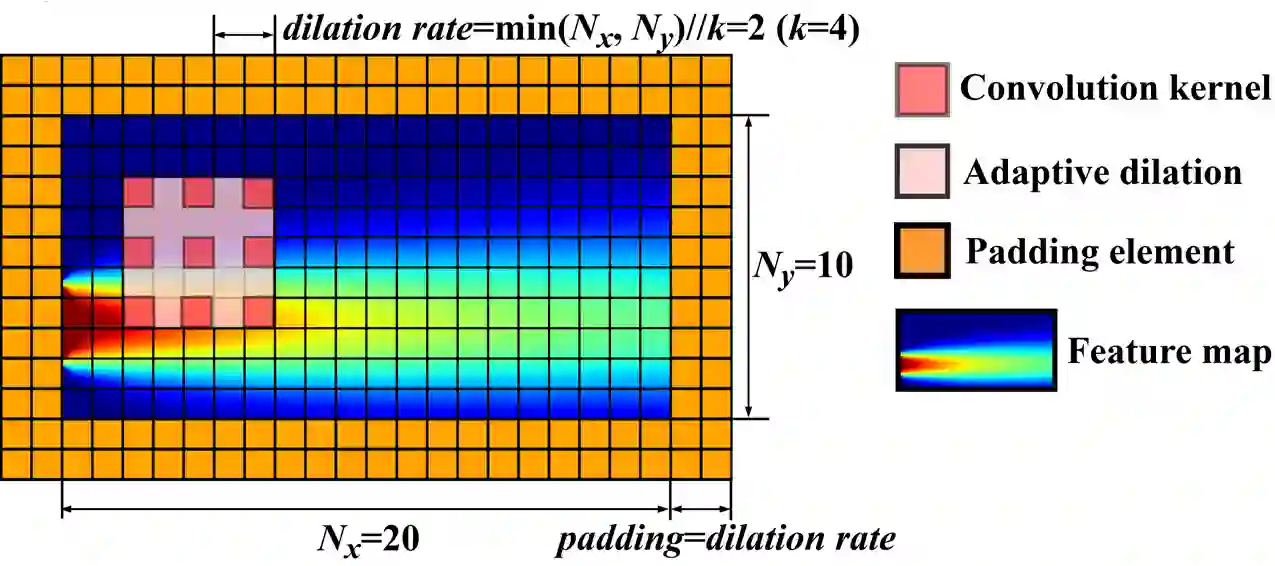
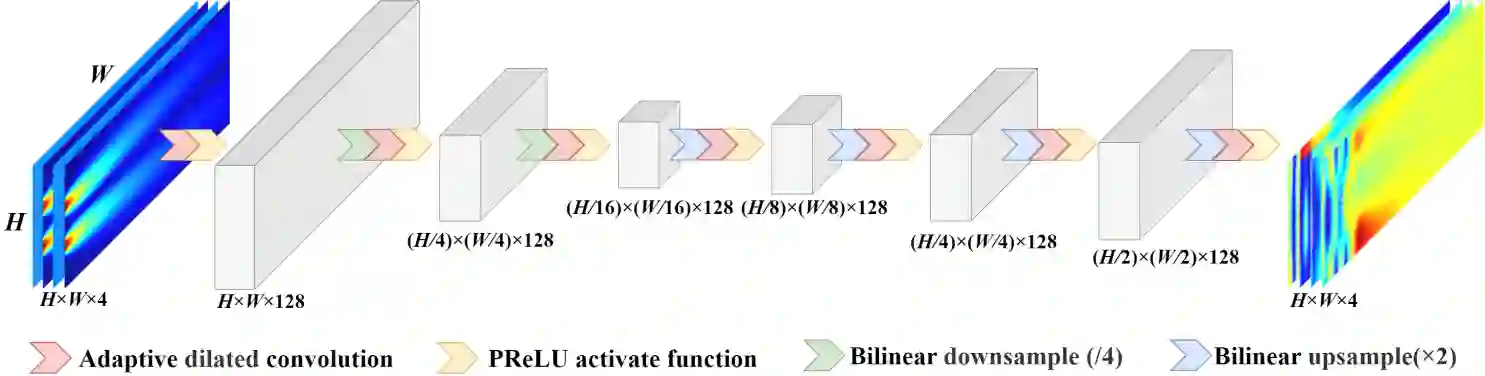
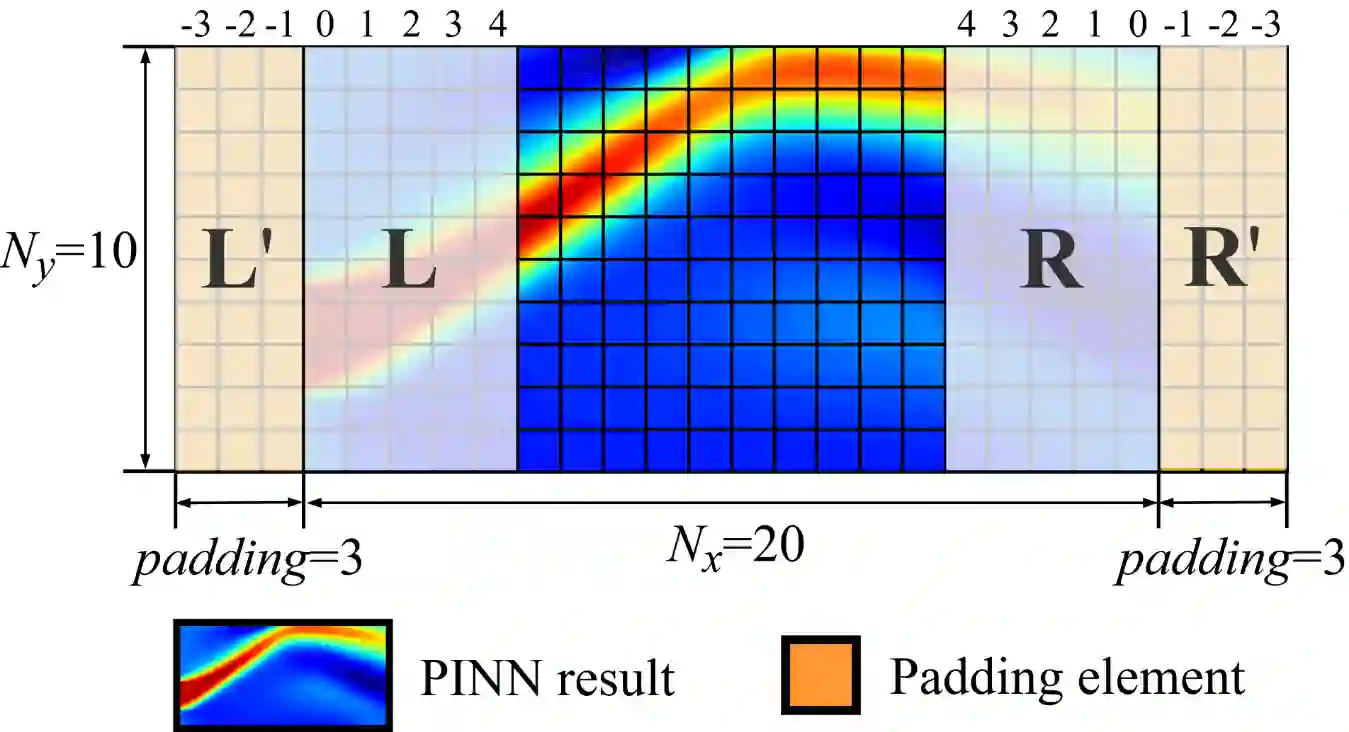
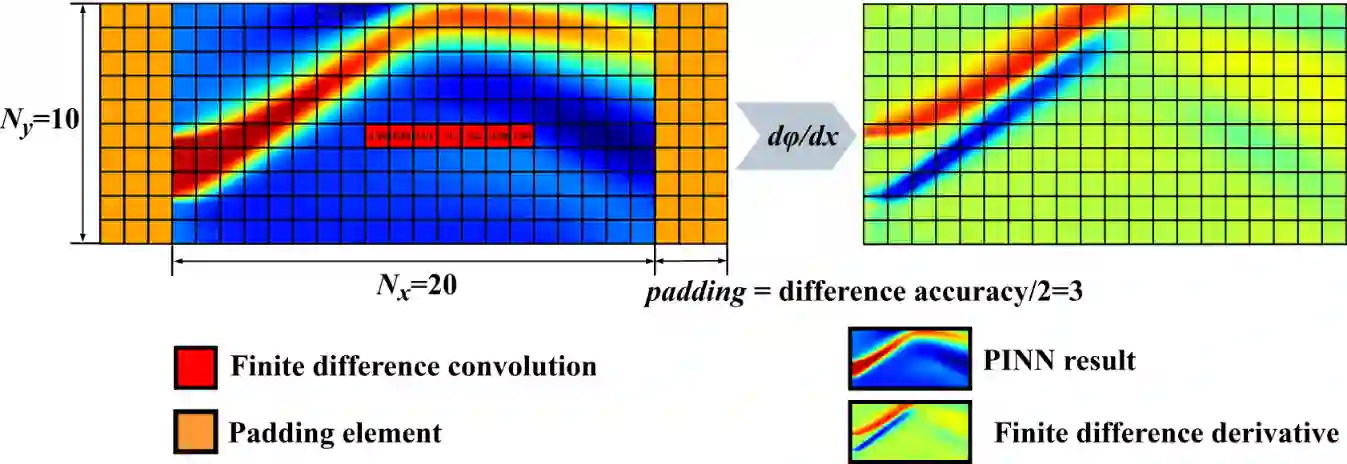
Compared with conventional numerical approaches to solving partial differential equations (PDEs), physics-informed neural networks (PINN) have manifested the capability to save development effort and computational cost, especially in scenarios of reconstructing the physics field and solving the inverse problem. Considering the advantages of parameter sharing, spatial feature extraction and low inference cost, convolutional neural networks (CNN) are increasingly used in PINN. However, some challenges still remain as follows. To adapt convolutional PINN to solve different PDEs, considerable effort is usually needed for tuning critical hyperparameters. Furthermore, the effects of the finite difference accuracy, and the mesh resolution on the predictivity of convolutional PINN are not settled. To fill the gaps above, we propose three initiatives in this paper: (1) A Multi-Receptive-Field PINN (MRF-PINN) model is established to solve different types of PDEs on various mesh resolutions without manual tuning; (2) The dimensional balance method is used to estimate the loss weights when solving Navier-Stokes equations; (3) The Taylor polynomial is used to pad the virtual nodes near the boundaries for implementing high-order finite difference. The proposed MRF-PINN is tested for solving three typical linear PDEs (elliptic, parabolic, hyperbolic) and a series of nonlinear PDEs (Navier-Stokes PDEs) to demonstrate its generality and superiority. This paper shows that MRF-PINN can adapt to completely different equation types and mesh resolutions without any hyperparameter tuning. The dimensional balance method saves computational time and improves the convergence for solving Navier-Stokes PDEs. Further, the solving error is significantly decreased under high-order finite difference, large channel number, and high mesh resolution, which is expected to be a general convolutional PINN scheme.
翻译:与解决部分差异方程式(PDEs)的常规数字方法相比,物理学知情神经网络(PINN)显示出了节省开发努力和计算成本的能力,特别是在重建物理场和解决逆向问题的情景中。考虑到参数共享、空间特征提取和低推论成本的优点,进化神经网络(CNN)越来越多地用于PINN。然而,一些挑战依然存在。要调整卷进 PINN以解不同的PDEs,通常需要做出相当大的努力来调整临界超参数。此外,有限差异精确度和网状智能分辨率对共振PINN的预测性效果和计算成本。为了填补上述空白,我们在本文中提出了三项举措:(1) 多感-感-战型 PINN(MRF-PINN)模型用于解决各种纸质分辨率分辨率的不同类型PDIS,在解决Navi-Stokeal-Scial等式方程式时,维度平衡方法可用于估算损失重量;(3) 典型的PDOL-al-deal-al-deal-deal deal deal demodal dismal demodal disal demodal demodal demodes a mess deal demode demodeal demods mess demodal demodal demodal demods mal demods mis mess mess mal deal demo ma ro ro ro ro 。 。Tal demodal demodal demodal demodal demo 任何高, 。