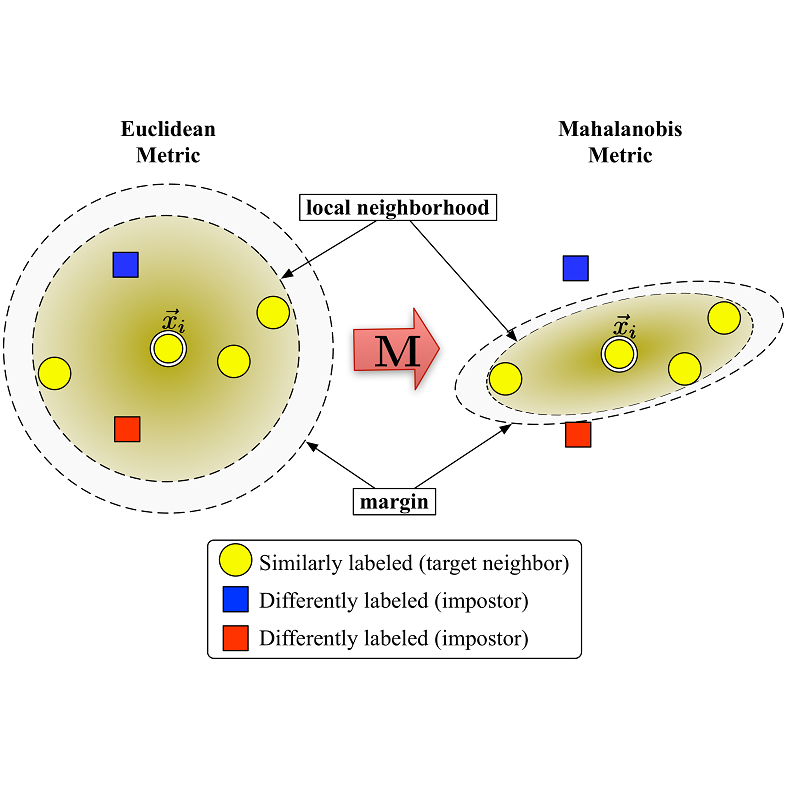
Good quality similarity metrics can significantly facilitate the performance of many large-scale, real-world applications. Existing studies have proposed various solutions to learn a Mahalanobis or bilinear metric in an online fashion by either restricting distances between similar (dissimilar) pairs to be smaller (larger) than a given lower (upper) bound or requiring similar instances to be separated from dissimilar instances with a given margin. However, these linear metrics learned by leveraging fixed bounds or margins may not perform well in real-world applications, especially when data distributions are complex. We aim to address the open challenge of "Online Adaptive Metric Learning" (OAML) for learning adaptive metric functions on the fly. Unlike traditional online metric learning methods, OAML is significantly more challenging since the learned metric could be non-linear and the model has to be self-adaptive as more instances are observed. In this paper, we present a new online metric learning framework that attempts to tackle the challenge by learning an ANN-based metric with adaptive model complexity from a stream of constraints. In particular, we propose a novel Adaptive-Bound Triplet Loss (ABTL) to effectively utilize the input constraints and present a novel Adaptive Hedge Update (AHU) method for online updating the model parameters. We empirically validate the effectiveness and efficacy of our framework on various applications such as real-world image classification, facial verification, and image retrieval.
翻译:现有研究提出了各种解决方案,以在线方式学习马哈拉诺比或双线度量,其方法是将类似(不同)对的距离限制在比某一较低(上调)约束的更小(大)比某一较低(上调)约束的更小(大),或要求将类似情况与特定差幅的不同情况区分开来。然而,这些通过利用固定界限或边距而学到的线性指标在现实世界应用程序中可能无法很好地发挥作用,特别是在数据分布复杂的情况下。我们的目的是应对“在线适应性计量学习”(OAML)的公开挑战,以学习在飞上学习适应性计量功能。不同于传统的在线计量学习方法,OAML具有更大的挑战性,因为所学的衡量标准可能是非线性,而且该模型在更多情况下必须自我适应性。在本文中,我们提出了一个新的在线指标学习框架,试图通过学习具有适应性模型复杂性的模型来应对挑战。我们特别建议采用新式的适应性-调整性矩阵更新标准,作为新的模型,并有效地更新我们采用各种标准性格式的升级性标准,以便有效地更新我们的新格式更新模型和不断更新。