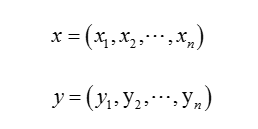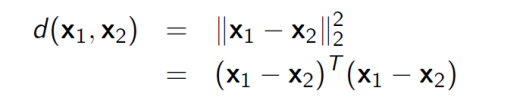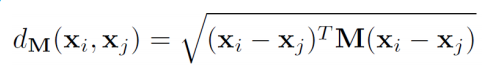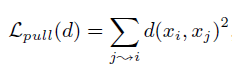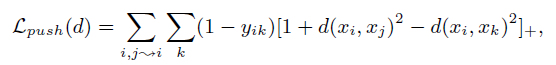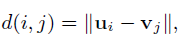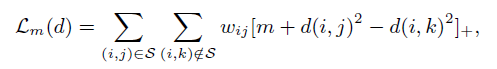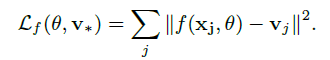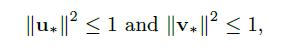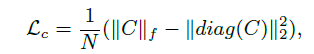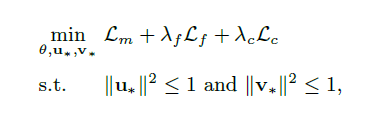LibRec 每周算法：Collaborative Metric Learning (WWW'17)

本周介绍WWW 2017的文章：Collaborative Metric Learning，其核心是将Metric Learning和Collaborative Filtering结合提升推荐效果。

Cheng-Kang Hsieh, Longqi Yang,Yin Cui, et al., Collaborative Metric Learning, WWW 2017

本文指出基于矩阵分解的CF模型使用点积度量user vector与 item vector的方式不满足三角不等式，导致MF模型无法捕获用户的细粒度偏好。因此提出使用Large-Margin Nearest Neighbor（LMNN）中提到的异类远离思想， 即一个用户所喜欢的商品要远离这个用户不喜欢的物品。并且该距离会被一个与Rank（物品的排序）有关的权重控制，文章中进一步考虑了使用deep learning 进行特征映射，正则项约束，协方差正则化等。最终，在一系列标准数据集上进行测试，发现提出的算法性能提升明显。

距离度量

---

概念：相似性（距离）度量简单讲就是一种比较两个对象相似程度的工具，例如比较人脸的相似性、人体姿势的相似性，也可用于图像搜索等应用。

一般需要根据处理的问题选择合适的相似性度量函数d(x,y)，其满足的条件为：

常见的相似性度量方法主要有： 欧氏距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离、马氏距离、夹角余弦、信息熵等。相似性度量描述两个对象之间的相似程度，假设特征向量x和y分别表示为：

相似度度量函数d(x,y)表示x和y之间的距离，d(x,y)越小表示x和y越相似。

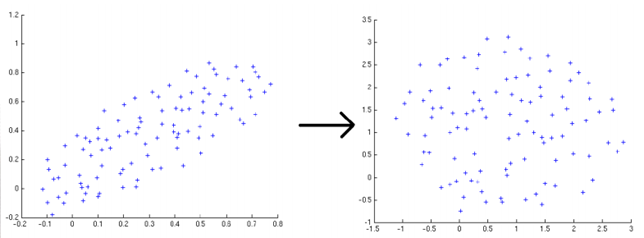
距离度量可以理解为相似度， 任何方法只要用到相似度，就会涉及到度量学习。度量学习的目的就是使得相似的样本距离更小，不相似的样本距离更大，如图（左图为欧式距离，右图为马氏距离）：

由于人的面部识别、姿态识别、步态识别甚至行为识别等特征的维度之间往往具有很强的相关性，因此度量学习的主流就是马氏距离学习。欧氏距离源自欧式空间中两个点之间的距离公式，其计算公式为（语义信息）：

而马氏距离（协方差信息）的定义为：

Large-Margin Nearest Neighbor（LMNN）

---

Lpull项定义（同类聚合）：

其中i是j的target neighbor，Lpush表示所有target neighbor对距离之和。

Lpush项定义（异类远离）：

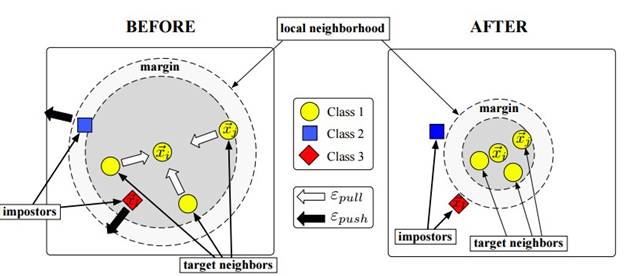
基本原理， 如图所示：

Collaborative Metric Learning（CML）

---

本文使用ui与vi分别作为用户与物品的特征描述。定义用户ui与vi之前距离，使用的是欧式距离：

Loss function为：

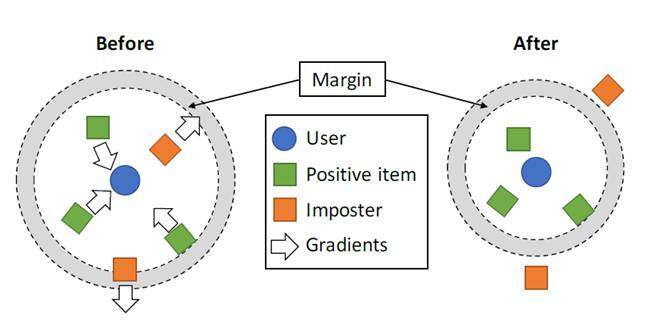
其中，用户i喜欢物品j，同时用户i不喜欢物品j，[z]+表示铰链损失（合叶损失函数），wij表示排名的权重。m表示安全距离，可以将相关对集合S与不相关的数据对分离开来。如下图所示：

图中含义非常明显：对于User喜欢的物品（Positive item），其渐变向User移动。同时，User不喜欢的物品，在计算的过程中，会逐渐从向外移动，直到被推出外围一个安全的距离（m）。

其原理与Weinberger的Metic learning经典文章(large margin nearest neighbor)LMNN[1]的方式非常相似，但本文提到的loss function与LMNN有三点不同：

• User的目标邻居（target neighbors）为用户喜欢的所有items，items没有目标邻居。CML是以每一个User作为一个分类标签，items只属于某个特定的类。

• CML没有Lpull, 只保留了Lpush项。item可以被很多user喜欢，最小化Lpull明显是不合理的。

• 本文采用加权的排名损失（weighted ranking loss）优化Top-K recommendations。

Approximated Ranking Weight

本小节提到对用户的low rank进行penalize（距离直接利用欧式距离，惩罚采用WARP）。low rank可以理解为User的推荐item列表的位置靠后的item。low rank penalize的目的就是通过给rank(i,j)大的样本更大的权重wij，使得在训练的过程中更加重视这些样本。rank越大，惩罚越大。同时， 本小节介绍了如何计算pairwise样本的权重Wij， 文中提到的计算方式：

• 对于每一个user-item 对，并行采样U对negative items，并计算hinge loss

• rank(i, j)的值为J*M/U向下取整

Integrating Item Features， Regularization and Training Procedure

本小节使用deep learing学习将物品feature到物品的latent vector的映射函数(transformation function)f(x), 解决Cold-Start问题。L2 损失函数的定义：

另外，选择合适的正则化方式对于提出的Model非常重要， 一方面， 所有用户与物品特征必须满足以下条件：

以确保metric的鲁棒性。

另一方面，使用协方差正则化[2]，Loss Lc的定义如下：

最终模型主要有三部分组成（Metric Learing部分，Deep Learing部分与正则化部分）：

其中lambda_f 与 lambda_c为超参数，作为loss function的损失函数。本文使用SGD最小化约束对象函数， 使用AdaGrad控制learning rating.

训练主要步骤：

实验评估

---

本文使用了6个不同领域的数据集：

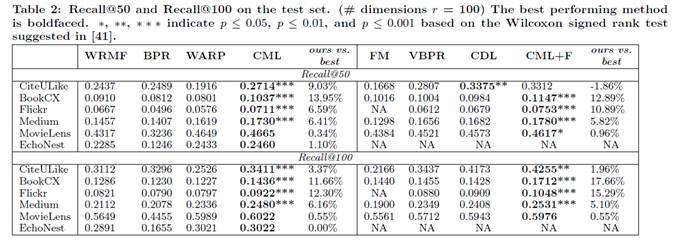
CML与两组baseline进行对比，结果为：

小结

本文提出CML，将Metric Learing与CF结合以提升推荐效果。根据论文中实验结果，在大部分情况下， CML性能提升明显。在实际生产环境中，需要根据具体的场景进行实验，有兴趣的读者可以研究下作者的源码。

https://github.com/changun/CollMetric 

猜您喜欢

LibRec 每周算法：ConvMF (RecSys'16)

LibRec 每周算法：CDL (KDD'15)

扩展阅读：Distance Metric Learning (DML)

1. Wikipedia for Metric

2. DML入门必读综述页面，分别介绍了Supervised Distance Metric Learning 与 Unsupervised Distance Metric Learning 经典方法，code与paper都可下载。其中她总结的Distance Metric Learning:A Comprehensive Survey非常有价值

3. ECCV 2010的turorial

4. Weinberger主页上有LMNN(Distance Metric Learning for Large Margin Nearest Neighbor Classification)的sclides和code

5. ITML(Information Throretic Metric Learning)。ITML是DML的经典算法，获得了ICML 2007的best paper award，对应的sclides[2]

参考资料

1. K. Q. Weinberger and L. K. Saul. Distance metric learning for large margin nearest neighbor classication. Journal of Machine Learning Research, 10(Feb):207-244, 2009.

2. M. Cogswell, F. Ahmed, R. Girshick, L. Zitnick, and D. Batra. Reducing overfitting in deep networks by decorrelating representations. ICLR'15, 2015.

3. http://column.hongliangjie.com/%E8%AF%BB%E8%AE%BA%E6%96%87/2017/04/16/www2017-cml/

4. http://rsarxiv.github.io/