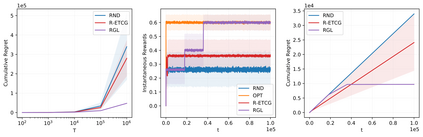
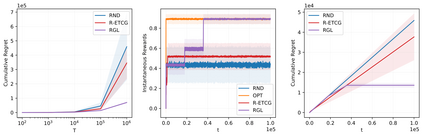
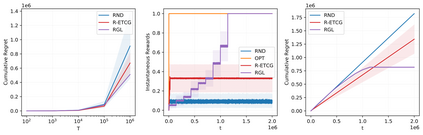
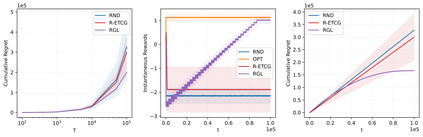
We investigate the problem of unconstrained combinatorial multi-armed bandits with full-bandit feedback and stochastic rewards for submodular maximization. Previous works investigate the same problem assuming a submodular and monotone reward function. In this work, we study a more general problem, i.e., when the reward function is not necessarily monotone, and the submodularity is assumed only in expectation. We propose Randomized Greedy Learning (RGL) algorithm and theoretically prove that it achieves a $\frac{1}{2}$-regret upper bound of $\tilde{\mathcal{O}}(n T^{\frac{2}{3}})$ for horizon $T$ and number of arms $n$. We also show in experiments that RGL empirically outperforms other full-bandit variants in submodular and non-submodular settings.
翻译:我们调查了不受限制的组合式多武装强盗问题,并提供了全带反馈和对亚模量最大化的随机奖励。 先前的工作调查了假设亚模量和单质的奖励功能的相同问题。 在这项工作中,我们研究了一个更为普遍的问题, 即当奖励功能不一定是单质的, 而亚模量的假设只是期望而已。 我们提出了随机的贪婪学习算法, 并在理论上证明它达到了美元( $\ frac{ 1 ⁇ 2} $- regret) 的上限 $\ tilde_ mathcal{O} (n T ⁇ frac{2 ⁇ 3}} $( $$) 和 军备数量$( $)。 我们还在实验中显示, RGL 在亚模量和非亚模量的环境中, 实验性贪婪在实验性地优于其他全带变体外变体。