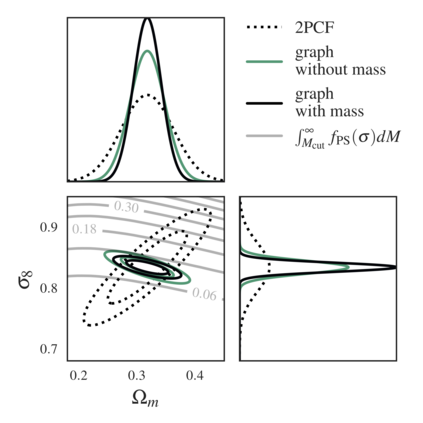
We present an implicit likelihood approach to quantifying cosmological information over discrete catalogue data, assembled as graphs. To do so, we explore cosmological parameter constraints using mock dark matter halo catalogues. We employ Information Maximising Neural Networks (IMNNs) to quantify Fisher information extraction as a function of graph representation. We a) demonstrate the high sensitivity of modular graph structure to the underlying cosmology in the noise-free limit, b) show that graph neural network summaries automatically combine mass and clustering information through comparisons to traditional statistics, c) demonstrate that networks can still extract information when catalogues are subject to noisy survey cuts, and d) illustrate how nonlinear IMNN summaries can be used as asymptotically optimal compressed statistics for Bayesian simulation-based inference. We reduce the area of joint $\Omega_m, \sigma_8$ parameter constraints with small ($\sim$100 object) halo catalogues by a factor of 42 over the two-point correlation function, and demonstrate that the networks automatically combine mass and clustering information. This work utilises a new IMNN implementation over graph data in Jax, which can take advantage of either numerical or auto-differentiability. We also show that graph IMNNs successfully compress simulations away from the fiducial model at which the network is fitted, indicating a promising alternative to n-point statistics in catalogue simulation-based analyses.
翻译:我们展示了一种隐含的可能性方法,用离散目录数据来量化宇宙信息,以图解形式收集。为此,我们利用模拟暗物质光环目录来探索宇宙参数限制。我们使用信息最大化神经网络(IMNNS)来量化渔业信息提取,以此作为图形表达法的函数。我们a)展示了模块图形结构对于无噪音限制的内在宇宙学的高度敏感性,b)显示图形神经网络摘要通过与传统统计的比较,自动将质量信息与集中信息结合起来;c)表明当目录受到紧张的调查削减时,网络仍然可以提取信息;d)说明如何使用非线性IMNN网摘要来对Bayesian模拟误判法使用非线性的最佳压缩统计数据。我们用小的(simm100 对象) 来减少模块图形图形结构结构结构结构结构的高度敏感度,通过基于42个系数将质量和组合信息自动组合起来。这项工作利用了新的IMNNNN网执行模型,在BA型目录中可以成功显示我们I号模拟数字的可靠性数据。