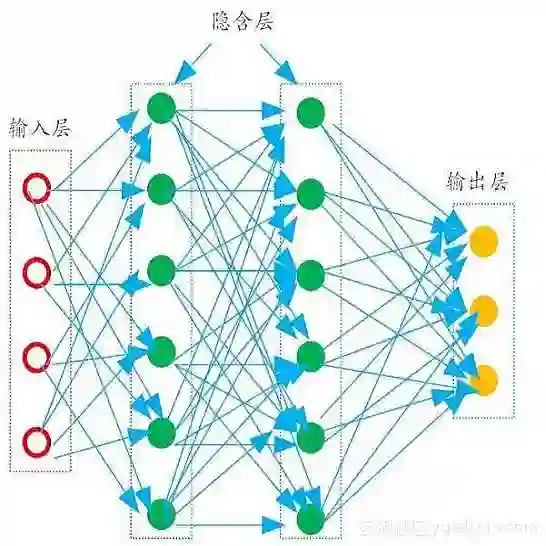
In this work, we firstly apply the Train-Tensor (TT) networks to construct a compact representation of the classical Multilayer Perceptron, representing a reduction of up to 95% of the coefficients. A comparative analysis between tensor model and standard multilayer neural networks is also carried out in the context of prediction of the Mackey-Glass noisy chaotic time series and NASDAQ index. We show that the weights of a multidimensional regression model can be learned by means of TT network and the optimization of TT weights is a more robust to the impact of coefficient initialization and hyper-parameter setting. Furthermore, an efficient algorithm based on alternating least squares has been proposed for approximating the weights in TT-format with a reduction of computational calculus, providing a much faster convergence than the well-known adaptive learning-method algorithms, widely applied for optimizing neural networks.
翻译:在这项工作中,我们首先应用培训-感官(TT)网络来构建经典多层倍数的缩略语,代表系数的减少幅度高达95%。在预测麦克奇-格拉斯噪音混乱的时间序列和NASDAQ指数的背景下,还进行了对高模模型和标准多层神经网络的比较分析。我们表明,可以通过TT网络来学习多维回归模型的重量,而优化TT重量对于系数初始化和超参数设置的影响更为有力。此外,还提议了一种基于交替最小方位的有效算法,用于对TT-格式中的重量进行近交比,同时减少计算积分,比为优化神经网络广泛应用的众所周知的适应性学习-方法算法更快。