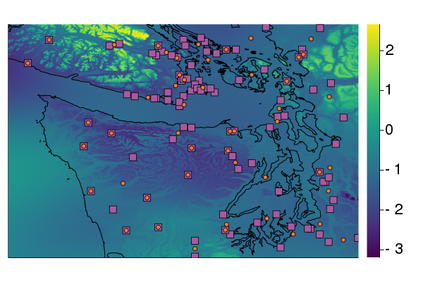
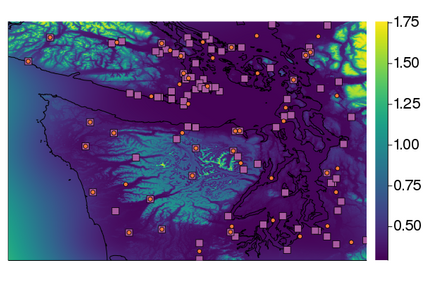
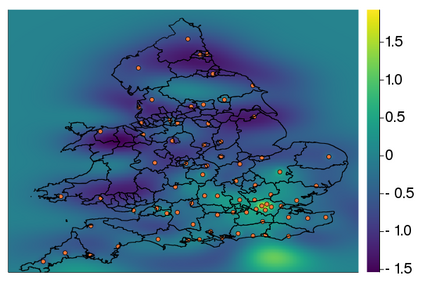
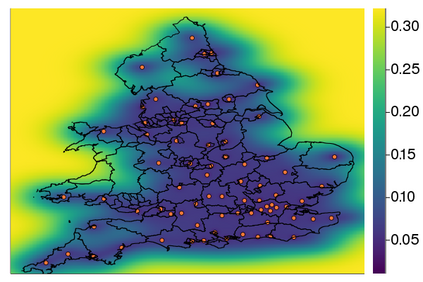
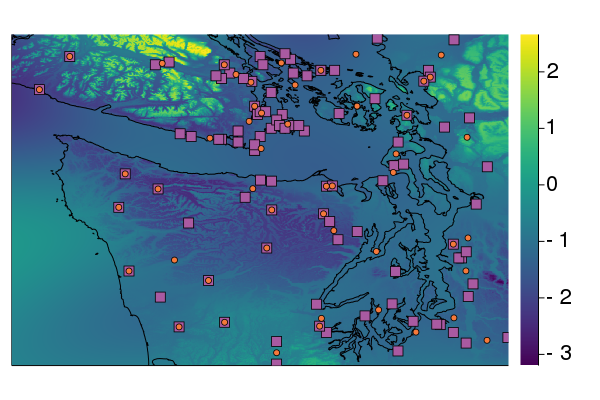
Gaussian processes (GPs) are important probabilistic tools for inference and learning in spatio-temporal modelling problems such as those in climate science and epidemiology. However, existing GP approximations do not simultaneously support large numbers of off-the-grid spatial data-points and long time-series which is a hallmark of many applications. Pseudo-point approximations, one of the gold-standard methods for scaling GPs to large data sets, are well suited for handling off-the-grid spatial data. However, they cannot handle long temporal observation horizons effectively reverting to cubic computational scaling in the time dimension. State space GP approximations are well suited to handling temporal data, if the temporal GP prior admits a Markov form, leading to linear complexity in the number of temporal observations, but have a cubic spatial cost and cannot handle off-the-grid spatial data. In this work we show that there is a simple and elegant way to combine pseudo-point methods with the state space GP approximation framework to get the best of both worlds. The approach hinges on a surprising conditional independence property which applies to space--time separable GPs. We demonstrate empirically that the combined approach is more scalable and applicable to a greater range of spatio-temporal problems than either method on its own.
翻译:Gausian 进程( GPs) 是气候科学和流行病学等时空建模问题中进行推断和学习的重要概率工具, 但是, 现有的 GP 近似值并不同时支持大量离网空间数据点和长时间序列, 它们是许多应用的标志。 Psedo-point 近似值是将GP推广到大型数据集的黄金标准方法之一, 非常适合处理离网空间数据。 但是, 它们无法处理长时观测前景, 有效地恢复到时间层面的立方计算缩放。 国家空间 GP 近似值非常适合处理时间数据。 如果 GP 之前的时空时端点接受马可夫形式, 导致时间观测数量的线性复杂性, 但却具有立方空间成本, 无法处理离网空间数据。 在这项工作中, 我们显示, 将假点方法与州空间GP 近似框架相结合, 以获得两个世界的最佳结果。 国家空间 GP 近似值方法取决于一个令人惊讶的有条件的独立度方法, 也就是我们所应用的范围更大的空间- 度方法。