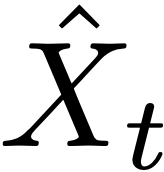In this study, we generalize a problem of sampling a scalar Gauss Markov Process, namely, the Ornstein-Uhlenbeck (OU) process, where the samples are sent to a remote estimator and the estimator makes a causal estimate of the observed realtime signal. In recent years, the problem is solved for stable OU processes. We present solutions for the optimal sampling policy that exhibits a smaller estimation error for both stable and unstable cases of the OU process along with a special case when the OU process turns to a Wiener process. The obtained optimal sampling policy is a threshold policy. However, the thresholds are different for all three cases. Later, we consider additional noise with the sample when the sampling decision is made beforehand. The estimator utilizes noisy samples to make an estimate of the current signal value. The mean-square error (mse) is changed from previous due to noise and the additional term in the mse is solved which provides performance upper bound and room for a pursuing further investigation on this problem to find an optimal sampling strategy that minimizes the estimation error when the observed samples are noisy. Numerical results show performance degradation caused by the additive noise.
翻译:在本研究中,我们概括了对标标Gaus Markov 进程取样的问题,即Ornstein-Uhlenbeck (OU) 进程,将样品送到远程估计器,而估计器对观察到的实时信号进行因果估计。近年来,问题为稳定的OU进程解决了。我们提出了最佳取样政策的解决办法,即Ou进程向Wiener进程转变时,对稳定和不稳定的Ou进程案例的估算误差较小。获得的最佳取样政策是一个阈值政策。然而,所有三个案例的阈值都不同。后来,我们考虑在事先作出取样决定时,对样品增加噪音。估计器使用噪音样品对当前信号值作出估计。平均方差差(mse)与以前相比,由于噪音而有所改变,而 mese的附加条件得到了解决,为进一步调查这一问题提供了最高性能和空间,以便找到最佳取样战略,在观察到的样品为摄氏度造成降解时尽量减少估计误差。