SARMA: Scalable Low-Rank High-Dimensional Autoregressive Moving Averages via Tensor Decomposition

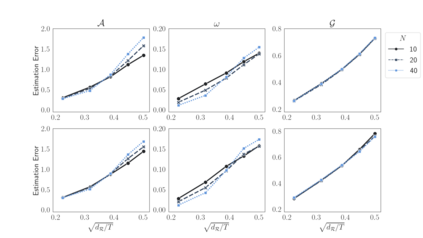
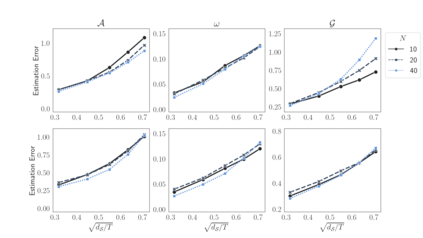
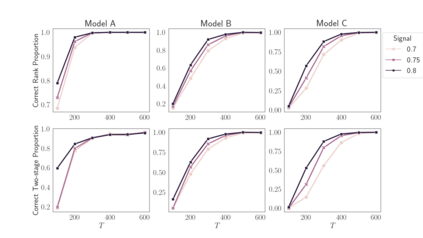
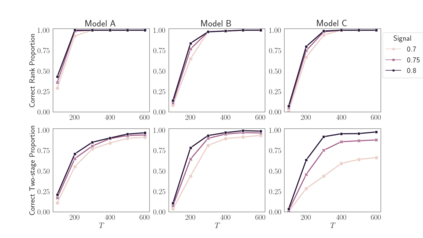
Existing models for high-dimensional time series are overwhelmingly developed within the finite-order vector autoregressive (VAR) framework, whereas the more flexible vector autoregressive moving averages (VARMA) have been much less considered. This paper introduces a high-dimensional model for capturing VARMA dynamics, namely the Scalable ARMA (SARMA) model, by combining novel reparameterization and tensor decomposition techniques. To ensure identifiability and computational tractability, we first consider a reparameterization of the VARMA model and discover that this interestingly amounts to a Tucker-low-rank structure for the AR coefficient tensor along the temporal dimension. Motivated by this finding, we further consider Tucker decomposition across the response and predictor dimensions of the AR coefficient tensor, enabling factor extraction across variables and time lags. Additionally, we consider sparsity assumptions on the factor loadings to accomplish automatic variable selection and greater estimation efficiency. For the proposed model, we develop both rank-constrained and sparsity-inducing estimators. Algorithms and model selection methods are also provided. Simulation studies and empirical examples confirm the validity of our theory and advantages of our approaches over existing competitors.