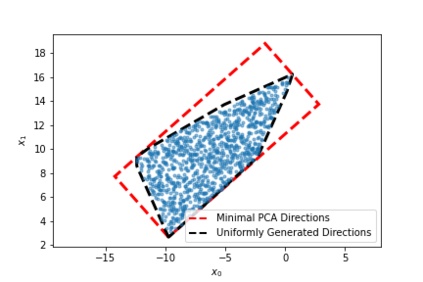
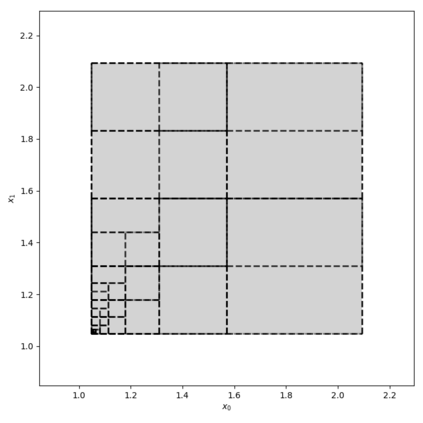
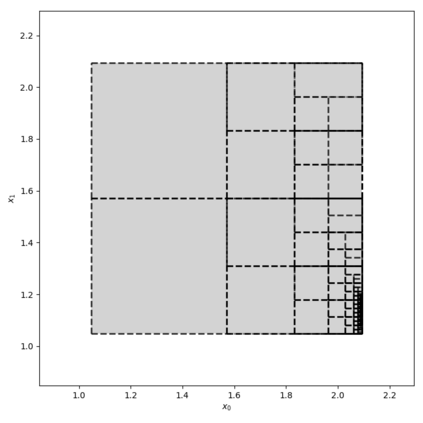
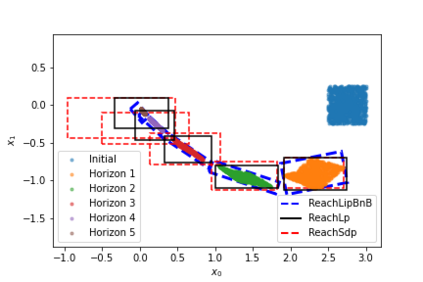
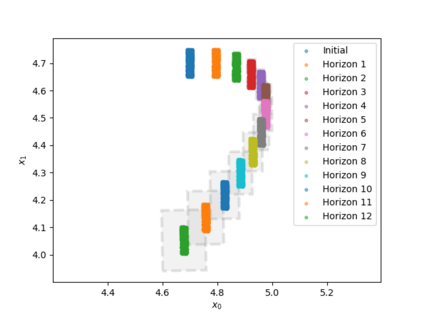
We propose a novel Branch-and-Bound method for reachability analysis of neural networks in both open-loop and closed-loop settings. Our idea is to first compute accurate bounds on the Lipschitz constant of the neural network in certain directions of interest offline using a convex program. We then use these bounds to obtain an instantaneous but conservative polyhedral approximation of the reachable set using Lipschitz continuity arguments. To reduce conservatism, we incorporate our bounding algorithm within a branching strategy to decrease the over-approximation error within an arbitrary accuracy. We then extend our method to reachability analysis of control systems with neural network controllers. Finally, to capture the shape of the reachable sets as accurately as possible, we use sample trajectories to inform the directions of the reachable set over-approximations using Principal Component Analysis (PCA). We evaluate the performance of the proposed method in several open-loop and closed-loop settings.
翻译:我们提出一个新的分支和组合方法,用于在开放环和封闭环设置下对神经网络进行可达性分析。 我们的想法是首先使用一个共振程序,在离线的某些利益方向下计算神经网络的利普施茨常数的精确边框。 然后我们用这些边框来利用利普施茨连续性参数获得可达性集的瞬时但保守的多元近距离。 为了减少保守性, 我们将我们的约束算法纳入分流战略, 以减少任意的偏差。 然后我们推广我们的方法, 以便用神经网络控制器对控制系统进行可达性分析。 最后, 为了尽可能准确地捕捉可达性组的形状, 我们使用样本轨迹, 用主元件分析( PCA) 来告知可达性可达性集的超兼容性组合的方向。 我们用主元件分析( PCA) 来评估拟议方法在若干开放环和闭环环境中的性能。