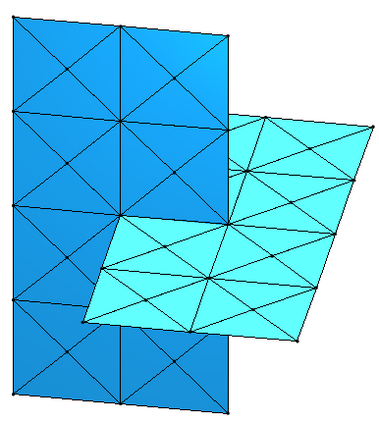
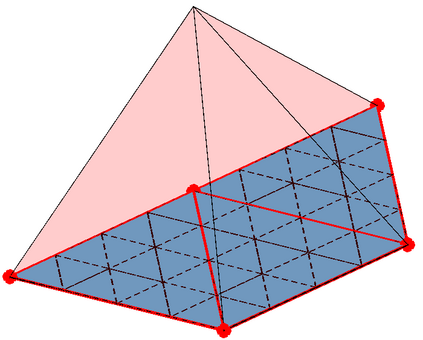
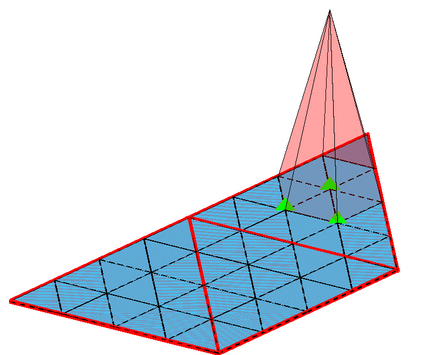
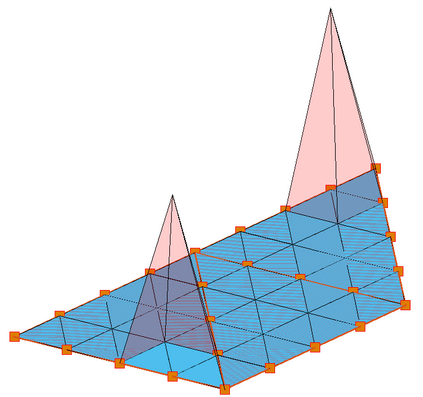
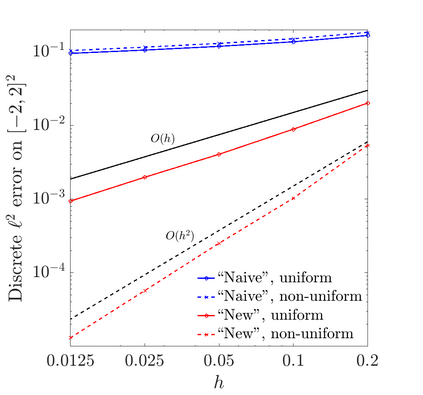
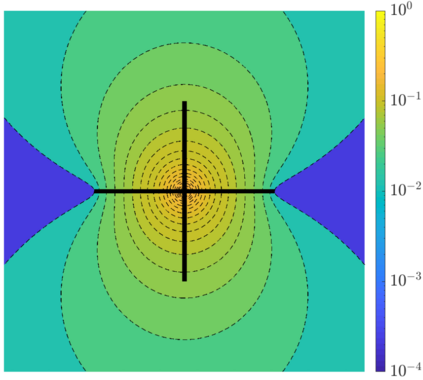
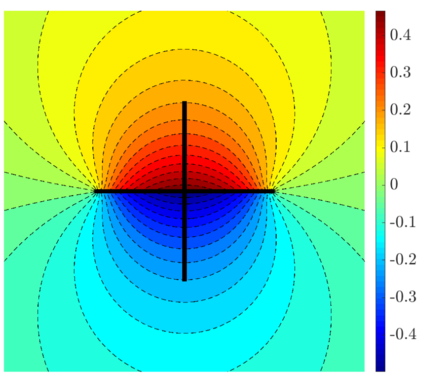
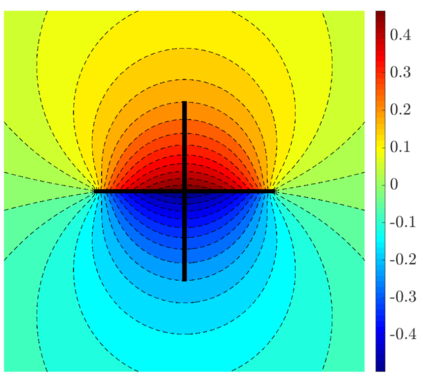
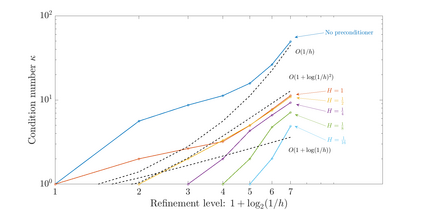
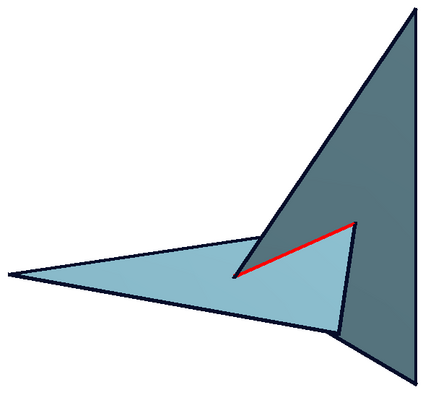
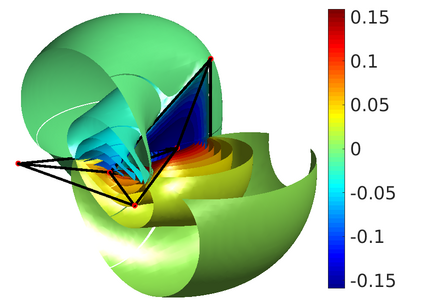
We present a preconditioning method for the linear systems arising from the boundary element discretization of the Laplace hypersingular equation on a $2$-dimensional triangulated surface $\Gamma$ in $\mathbb{R}^3$. We allow $\Gamma$ to belong to a large class of geometries that we call polygonal multiscreens, which can be non-manifold. After introducing a new, simple conforming Galerkin discretization, we analyze a substructuring domain-decomposition preconditioner based on ideas originally developed for the Finite Element Method. The surface $\Gamma$ is subdivided into non-overlapping regions, and the application of the preconditioner is obtained via the solution of the hypersingular equation on each patch, plus a coarse subspace correction. We prove that the condition number of the preconditioned linear system grows poly-logarithmically with $H/h$, the ratio of the coarse mesh and fine mesh size, and our numerical results indicate that this bound is sharp. This domain-decomposition algorithm therefore guarantees significant speedups for iterative solvers, even when a large number of subdomains is used.
翻译:暂无翻译