Tangling-Untangling Cycle for Efficient Learning

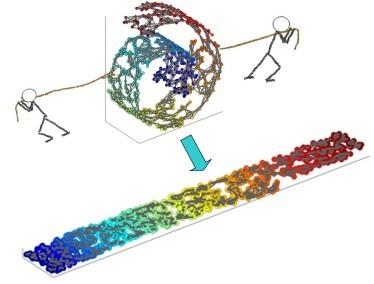
The conventional wisdom of manifold learning is based on nonlinear dimensionality reduction techniques such as IsoMAP and locally linear embedding (LLE). We challenge this paradigm by exploiting the blessing of dimensionality. Our intuition is simple: it is easier to untangle a low-dimensional manifold in a higher-dimensional space due to its vastness, as guaranteed by Whitney embedding theorem. A new insight brought by this work is to introduce class labels as the context variables in the lifted higher-dimensional space (so supervised learning becomes unsupervised learning). We rigorously show that manifold untangling leads to linearly separable classifiers in the lifted space. To correct the inevitable overfitting, we consider the dual process of manifold untangling -- tangling or aliasing -- which is important for generalization. Using context as the bonding element, we construct a pair of manifold untangling and tangling operators, known as tangling-untangling cycle (TUC). Untangling operator maps context-independent representations (CIR) in low-dimensional space to context-dependent representations (CDR) in high-dimensional space by inducing context as hidden variables. The tangling operator maps CDR back to CIR by a simple integral transformation for invariance and generalization. We also present the hierarchical extensions of TUC based on the Cartesian product and the fractal geometry. Despite the conceptual simplicity, TUC admits a biologically plausible and energy-efficient implementation based on the time-locking behavior of polychronization neural groups (PNG) and sleep-wake cycle (SWC). The TUC-based theory applies to the computational modeling of various cognitive functions by hippocampal-neocortical systems.