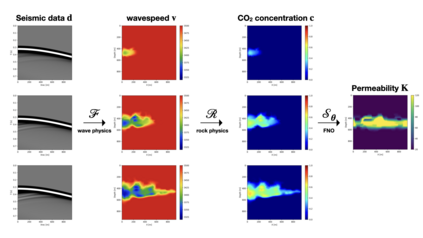
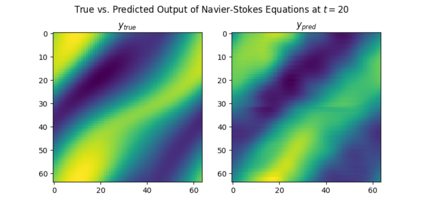
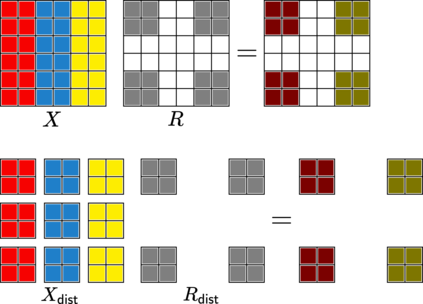
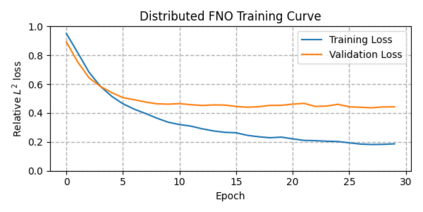
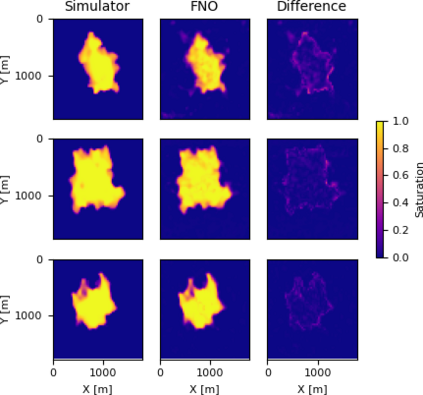
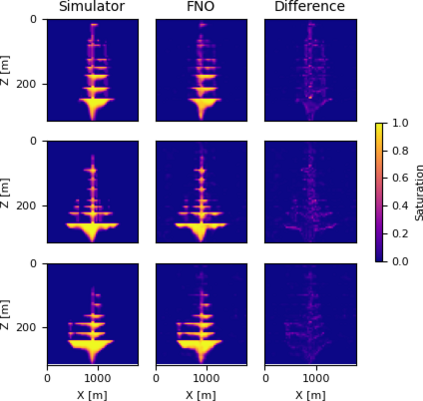
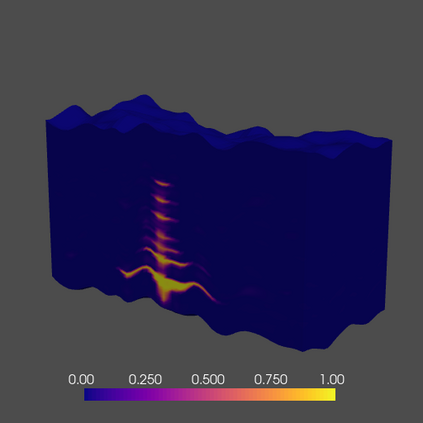
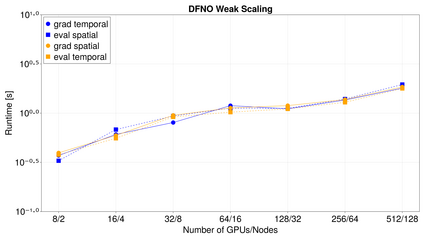
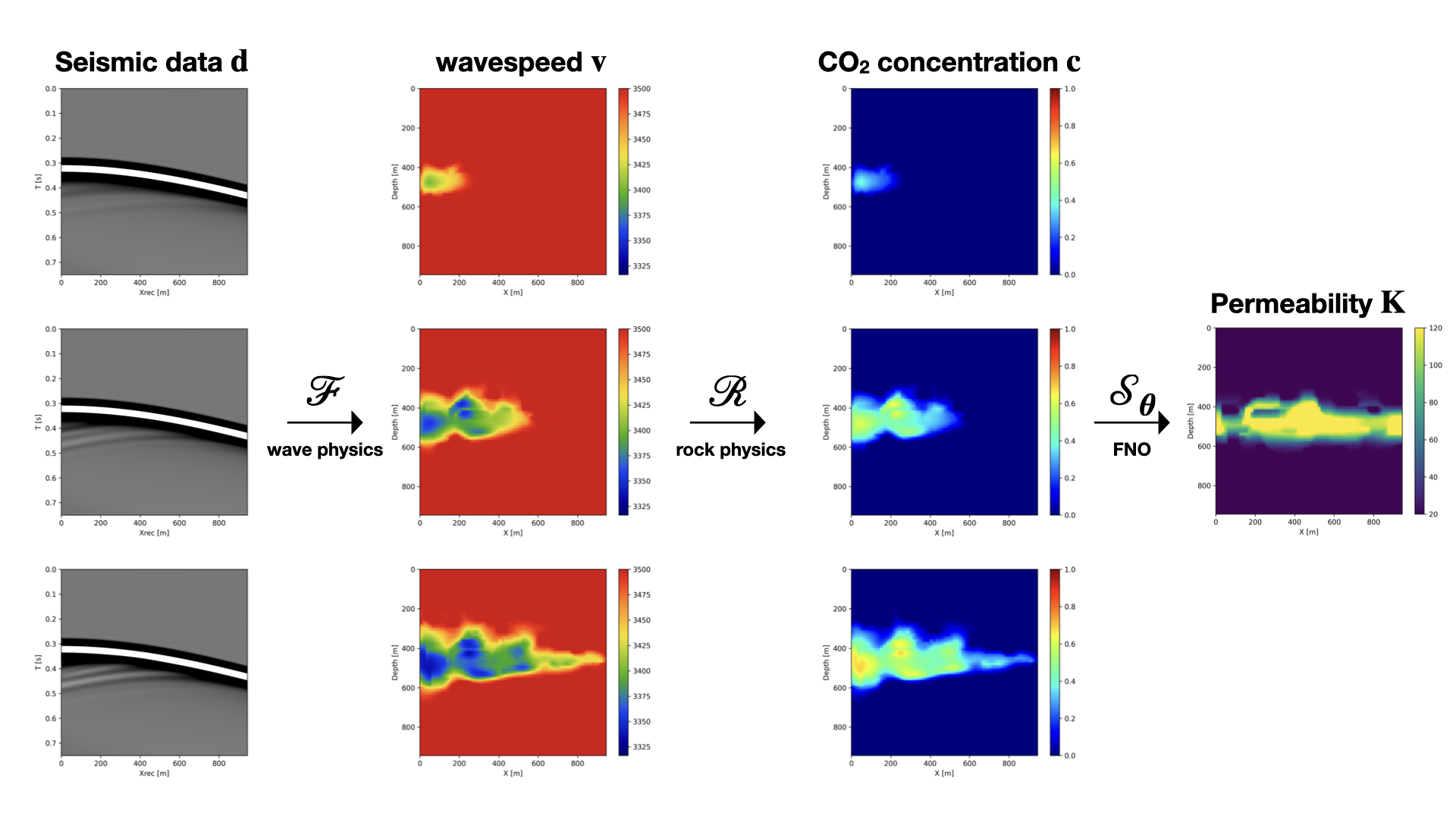
Fourier neural operators (FNOs) are a recently introduced neural network architecture for learning solution operators of partial differential equations (PDEs), which have been shown to perform significantly better than comparable deep learning approaches. Once trained, FNOs can achieve speed-ups of multiple orders of magnitude over conventional numerical PDE solvers. However, due to the high dimensionality of their input data and network weights, FNOs have so far only been applied to two-dimensional or small three-dimensional problems. To remove this limited problem-size barrier, we propose a model-parallel version of FNOs based on domain-decomposition of both the input data and network weights. We demonstrate that our model-parallel FNO is able to predict time-varying PDE solutions of over 2.6 billion variables on Perlmutter using up to 512 A100 GPUs and show an example of training a distributed FNO on the Azure cloud for simulating multiphase CO$_2$ dynamics in the Earth's subsurface.
翻译:Fourier神经操作员(FNOs)是最近为学习局部差异方程式(PDEs)的解决方案操作员而引入的神经网络结构,其表现明显优于可比深层学习方法。经过培训,FNOs可以比常规的PDE解答器实现多个数量级的加速,但是,由于输入数据和网络重量的高度,FNOs迄今只应用于二维或小三维问题。为了消除这一有限的问题大小障碍,我们提议了一个基于输入数据和网络重量的域分解的FNOs模型-平行版本。我们证明,我们的FNO模型能够预测Pelmutter上超过26亿个变量的时间变化式PDE解决方案,使用多达512个A100GPUs,并展示了在Azure云上分发的用于模拟地球地下多级 CO$2美元动态的FNO的范例。