Tensorization: Creating and Utilising Multidimensional Datasets for Multiway Analysis and Tensorised Deep Neural Networks -- Python Tutorial and Survey

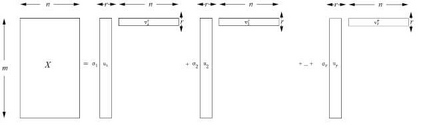
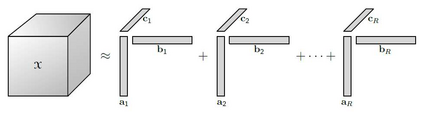
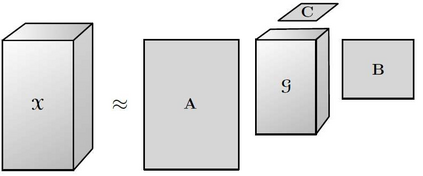
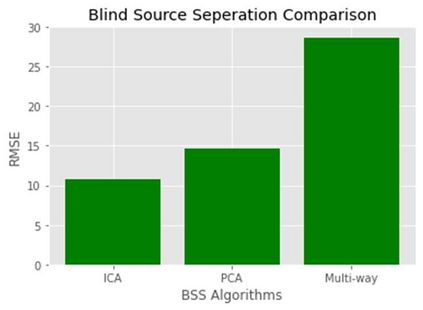
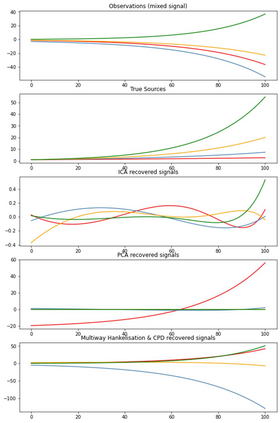
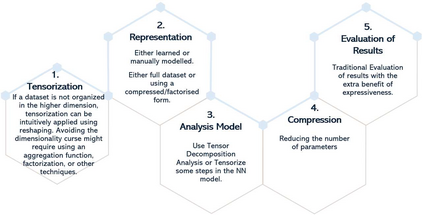
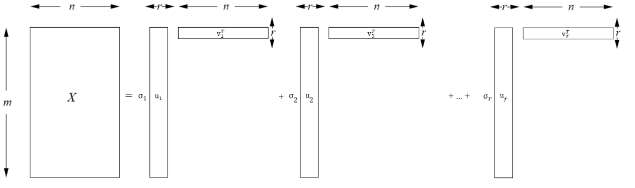
As the size and complexity of data continue to increase, the need for efficient and effective analysis methods becomes ever more crucial. Tensorization, the process of converting 2-dimensional datasets into multidimensional structures, has emerged as a promising approach for multiway analysis methods. This paper explores the steps involved in tensorization, multidimensional data sources, various multiway analysis methods employed, and the benefits of these approaches. A small example of Blind Source Separation (BSS) is presented comparing 2-dimensional algorithms and a multiway algorithm in Python. Results indicate that multiway analysis is more expressive. Additionally, tensorization techniques aid in compressing deep learning models by reducing the number of required parameters while enhancing the expression of relationships across dimensions. A survey of the multi-away analysis methods and integration with various Deep Neural Networks models is presented using case studies in different domains.