Learning latent causal graphs via mixture oracles

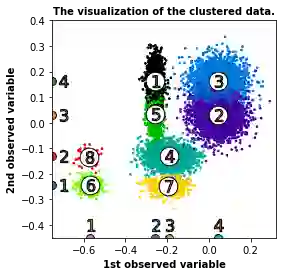
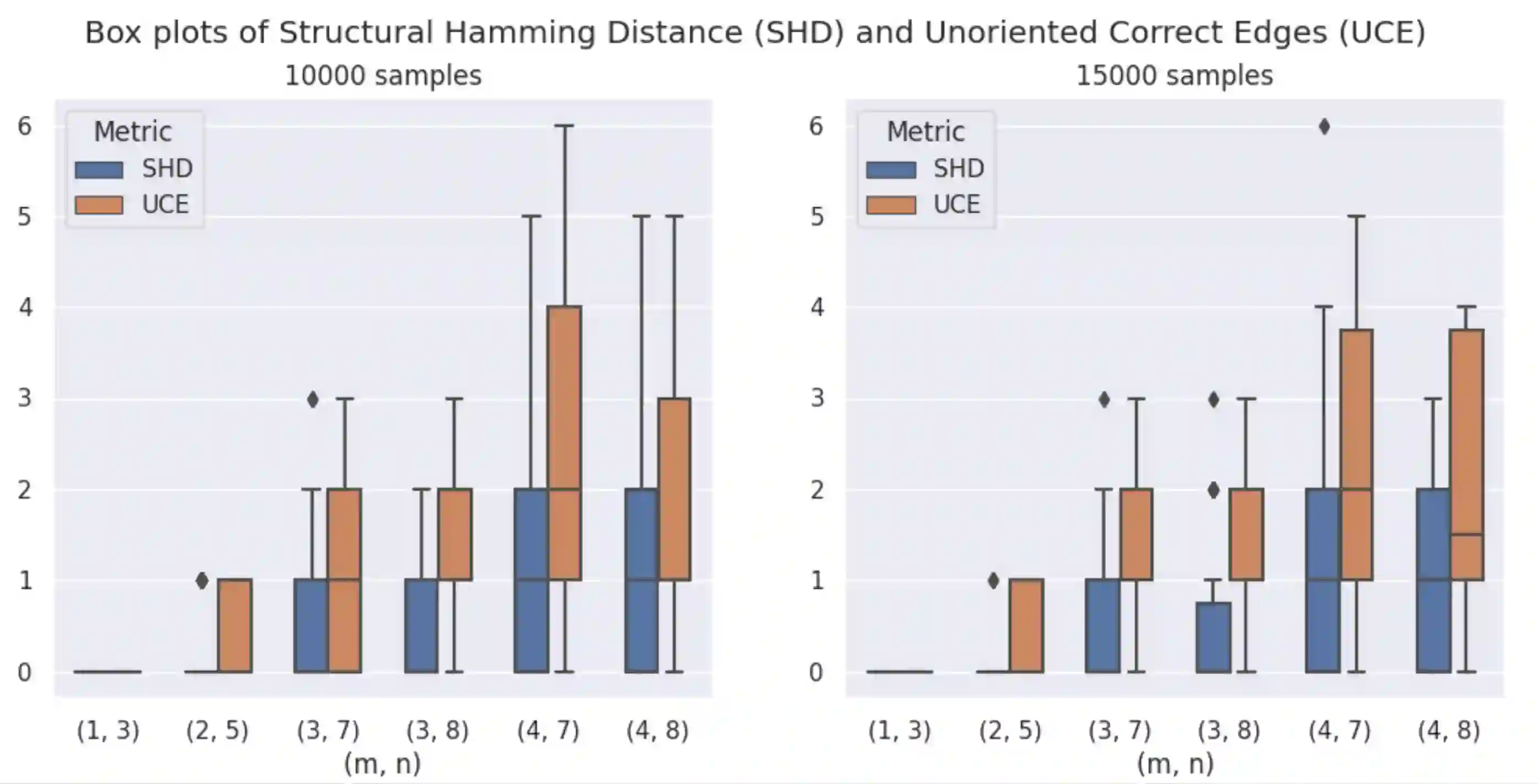
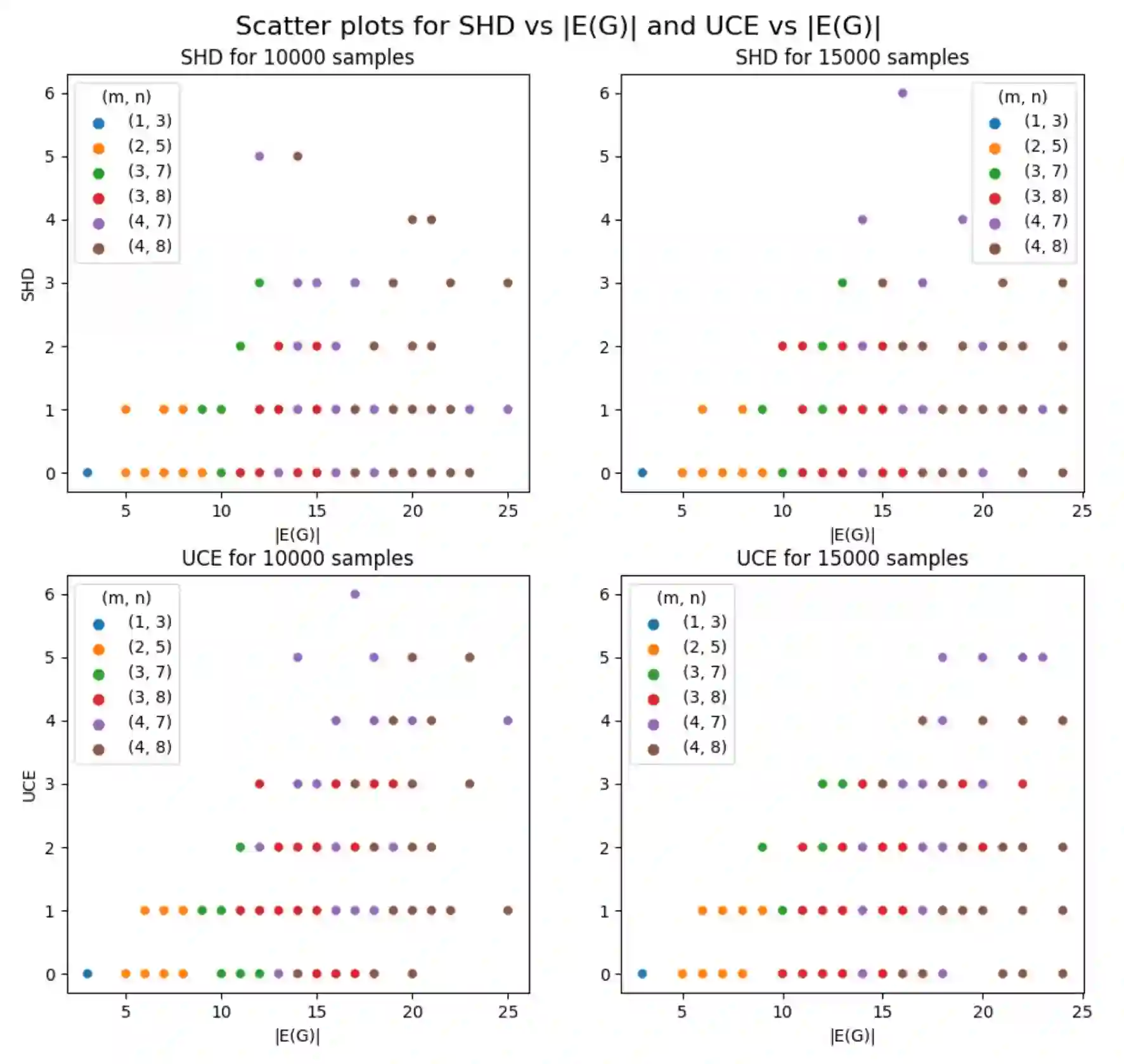
We study the problem of reconstructing a causal graphical model from data in the presence of latent variables. The main problem of interest is recovering the causal structure over the latent variables while allowing for general, potentially nonlinear dependence between the variables. In many practical problems, the dependence between raw observations (e.g. pixels in an image) is much less relevant than the dependence between certain high-level, latent features (e.g. concepts or objects), and this is the setting of interest. We provide conditions under which both the latent representations and the underlying latent causal model are identifiable by a reduction to a mixture oracle. The proof is constructive, and leads to several algorithms for explicitly reconstructing the full graphical model. We discuss efficient algorithms and provide experiments illustrating the algorithms in practice.