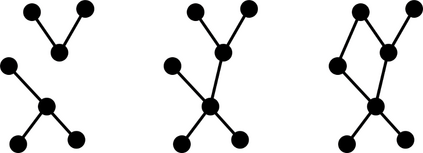
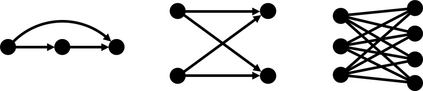
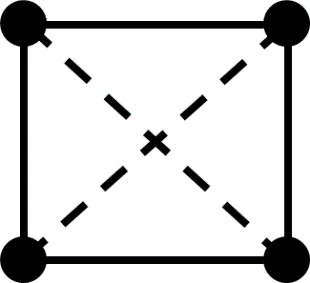
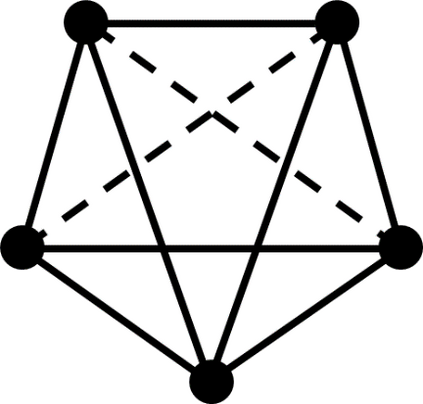
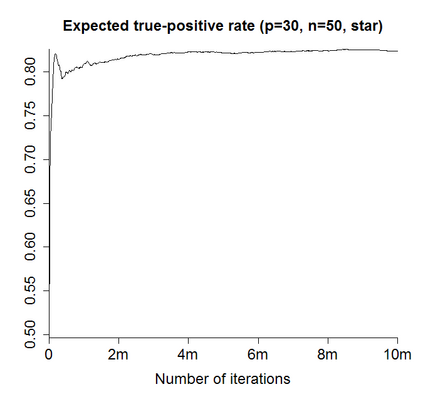
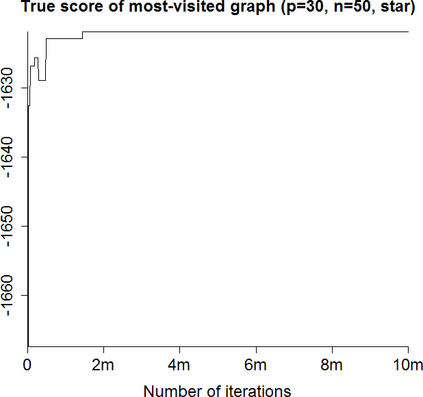
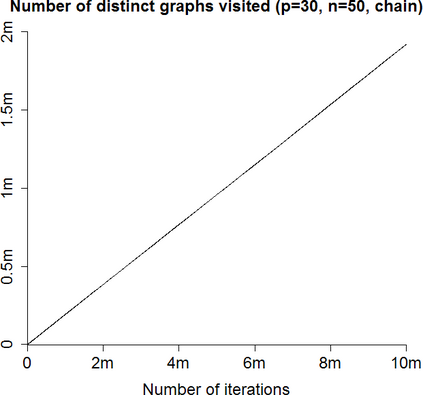
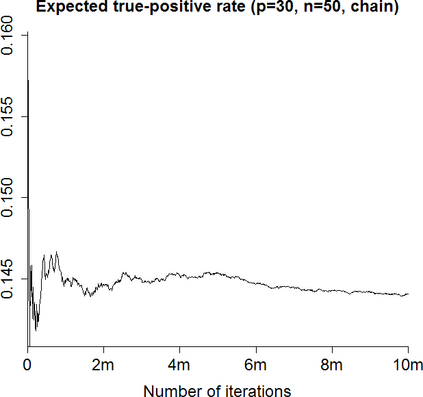
In Bayesian learning of Gaussian graphical model structure, it is common to restrict attention to certain classes of graphs and approximate the posterior distribution by repeatedly moving from one graph to another, using MCMC or methods such as stochastic shotgun search (SSS). I give two corrected versions of an algorithm for non-decomposable graphs and discuss random graph distributions, in particular as prior distributions. The main topic of the thesis is Bayesian structure-learning with forests or trees. Restricting attention to these graphs can be justified using theorems on random graphs. I describe how to use the Chow$\unicode{x2013}$Liu algorithm and the Matrix Tree Theorem to find the MAP forest and certain quantities in the posterior distribution on trees. I give adapted versions of MCMC and SSS for approximating the posterior distribution for forests and trees, and systems for storing these graphs so that it is easy to choose moves to neighbouring graphs. Experiments show that SSS with trees does well when the true graph is a tree or sparse graph. SSS with trees or forests does better than SSS with decomposable graphs in certain cases. Graph priors improve detection of hubs but need large ranges of probabilities. MCMC on forests fails to mix well and MCMC on trees is slower than SSS. (For a longer abstract see the thesis.)
翻译:在巴伊西亚州学习高山图形模型结构时,通常会限制对某些类别的图表的关注,并使用MCMCM或Stochactic 猎枪搜索等方法(SSS),通过反复从一个图表向另一个图表移动,限制对某些类别的图表的注意和近似事后分布的注意。我给出了两种非可分解的图表算法的更正版本,并讨论了随机图表分布,特别是先前的分布。论文的主要议题是用森林或树木进行巴伊西亚结构学习。使用随机图表的语标可以限制对这些图表的注意。我描述了如何使用Chow$\unicocode{x2013}Liu算法和Mas Track Tree理论来寻找MAP森林和树木分布中的某些数量。我提供了经调整的MCC和S SSS的版本,以及这些图表的储存系统,以便很容易选择向邻近的图表移动。实验显示,在真实的图表上,SSS的S的SS和树的失败状态比Sscarbreal Creal 还要好。在SSS的图中,Ssreareareal a a lader a graphles a pre coal be agoal be as be mass be a lax a mill be a mas a lad lad mas mass a lad mas a mas be a lase mas mass a mass a mas a mas mass a mas a ladre mas a lad lad lad lad lads a lads lads ladre maps a mas a lads a lads 需要在S.s.S.S.S.S.S.S.s mals mals mals mals mals mals mals mals mals mals mals mals mas as as as as mas mas as mas as as as mas mas mas mas mas mas mas mas mas mas mas mas